Dynamics of Julia Sets in Rational Maps
Control and Synchronization with Complex Perturbations
Abstract
This work deals with the study of the dynamical and fractal characteristics of the complex perturbed rational map provided by
The very fact of finding such a nonlinear method makes the realm of coordinated oscillations fresher and more interesting. The driving term associated with the optimal control function has, therefore, been substituted, whereby Julia sets, two belonging to synchronous systems, are evaluated. The buzz that follows this mathematical novelty significantly demands attention given its importance in understanding coupled dynamical systems in different settings. This elaborate introduction, therefore, sets-a-forward framework for the rigorous study of the control mechanisms and synchronization phenomena in complex perturbed rational maps.
Introduction
Fractals are widely studied for their ability to model complex phenomena, and Julia sets are prominent fractal structures in complex dynamics. These sets are defined as the closure of repelling periodic points of rational maps. For a rational map
Control of chaotic dynamics, including Julia sets, is critical for many applications. Existing control methods, such as the OGY method and Pyragas feedback, primarily stabilize finite fixed points. In this work, we adopt an optimal control function to regulate Julia sets, treating infinity as a fixed point. Synchronization of Julia sets, essential for understanding relations between different systems, is also explored by aligning their trajectories and fractal structures. This paper contributes to fractal control and synchronization by:
Introducing a control mechanism for Julia sets via the parameter
Demonstrating synchronization between two Julia sets associated with different parameters in the perturbed rational map.
These advancements provide insights into the interplay between fractal structures and complex dynamics, with implications for chaotic systems and their applications.
In the context of dynamical systems, Julia sets and Mandelbrot sets play a critical role in describing the long-term behavior of iterative processes. Their physical relevance emerges from their ability to model complex systems that exhibit chaotic or fractal-like behavior.
Julia Set and Mandelbrot Sets in Complex Systems
In the context of dynamical systems, Julia sets and Mandelbrot sets play a critical role in describing the long-term behavior of iterative processes. Their physical relevance emerges from their ability to model complex systems that exhibit chaotic or fractal-like behavior.
Julia Sets: The Boundary of Stability
A Julia set
Points in the complex plane that exhibit stable, predictable dynamics under a rational map
Points that diverge to infinity or exhibit chaotic behavior.
In a physical context:
Julia sets often represent systems that alternate between stable and chaotic regimes.
They serve as models for phase transitions, where the boundary represents critical points between phases.
In fields like optics, Julia sets help describe patterns in nonlinear systems, such as wave front distortions or light propagation through media.
Mandelbrot Sets: A Parameter-Space Map
The Mandelbrot set
It provides a visualization of stability regions in parameter space.
The Mandelbrot set predicts whether perturbations in a system lead to stability or chaos.
Together, Julia and Mandelbrot sets describe critical bifurcations and boundary behaviors, giving insights into systems where small changes in parameters can lead to drastically different outcomes.
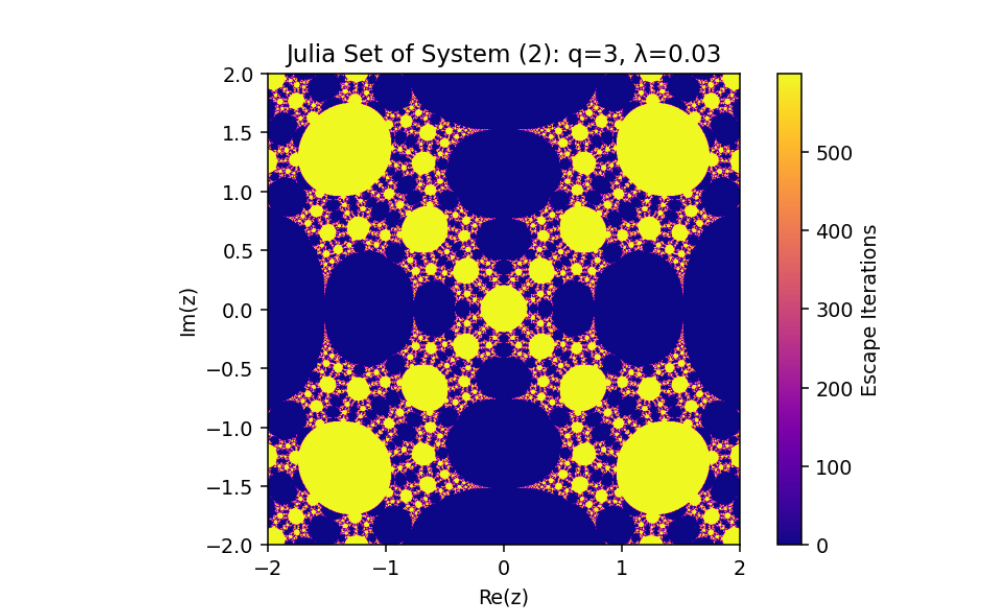
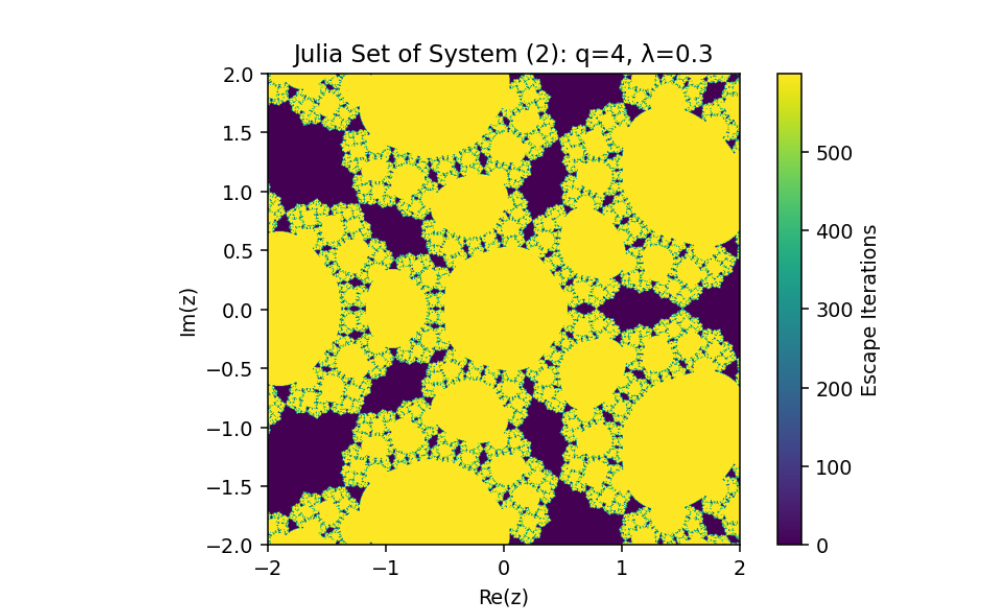
Generalized Dynamics
This work describes a generalization of Julia sets and their mathematical framework. This generalization introduces a perturbation parameter
Mathematical Definition:
Perturbed Rational Map:
where:
Impact of
For
For
Special Cases:
- When
- When
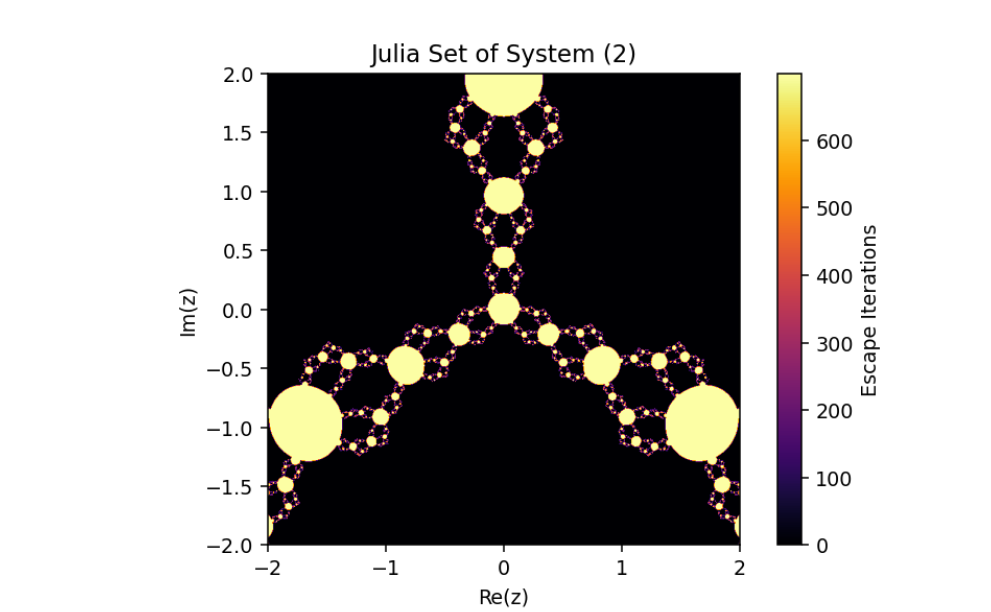
Rational Maps and Julia Sets
A rational map
Equivalently,
Escape Criterion
For a rational map
then all iterates of
Dynamics of the Perturbed Rational Map
The complex perturbed rational map studied is
When
This map generalizes rational maps
Fixed Points and Their Stability
In rational maps, fixed points satisfy
Attracting:
Repelling:
Neutral:
In this work, infinity acts as a fixed point, and its behavior is analyzed through escape criteria and control mechanisms.
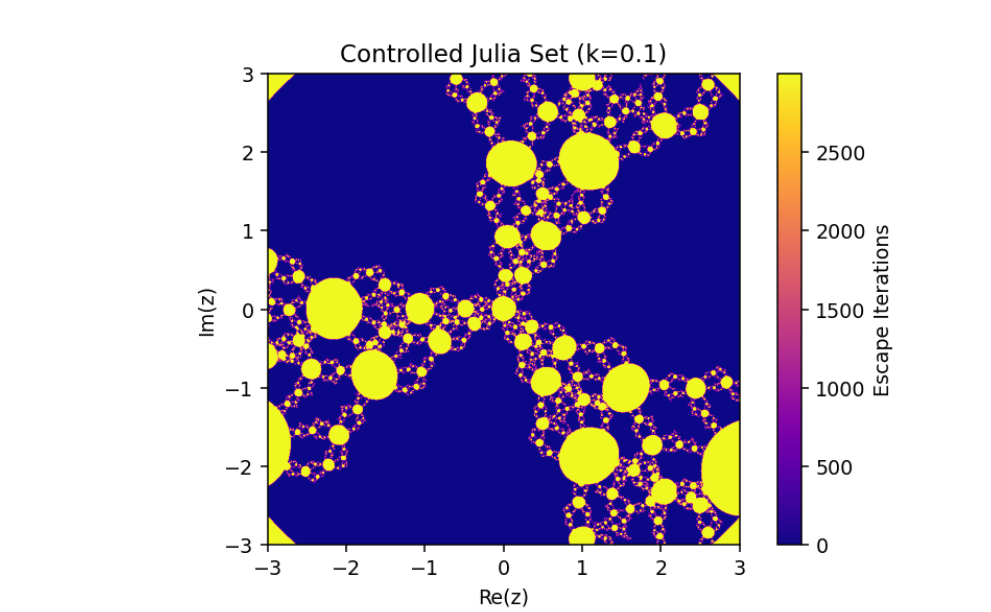
Control of Julia Set of the Complex Perturbed Rational System
Introducing a control mechanism to Julia sets opens new possibilities for exploring stability, bifurcation, and parameter sensitivity. The controlled rational map introduced earlier is a rich ground for experimentation and understanding dynamical behavior. In this section, we will delve deeper into the computational and algorithmic aspects of controlled Julia sets. A control parameter
Interpretation:
Base Map Contribution: The term
Feedback Control: The term
When
The Base System and Rational Map:
The base system is:
which can also be written as:
This is a rational map where:
The numerator
The denominator
Since the degree of
Introducing the Nonlinear Control:
To control the dynamics, a nonlinear control term
The controlled system becomes:
or equivalently:
Substitute
This is a concise symbolic representation called controlled rational map, and we define this following way:
Fixed Points and Behavior:
Fixed Points: The fixed points are solutions of
Rearrange:
Factorize:
Attracting Fixed Point: If
Escape Criterion:
That’s how we can write:
where
The control parameter
As
The escape criterion ensures iterates either escape to infinity or remain bounded within the Julia set boundary.
Optimal Control Function
The control function modifies the system to regulate its fractal properties. For the perturbed rational map:
Key results include:
With
This introduces a parameter
Generalized Map:
Iterative Function:
Boundedness Criterion:
A point
For practical purposes, we compute boundedness using an escape radius
If
Otherwise, it is bounded.
Key Parameters:
Mathematical Framework for Visualization
The study relies on the escape-time algorithm to visualize Julia sets:
Initialize a grid of points in the complex plane.
Iterate each point under the map
Assign colors based on the number of iterations required to escape a bounded region.
This technique provides insights into the influence of control parameters
Visualization Algorithm: Escape-Time Algorithm
Steps:
Initialize Grid:
- Define a grid of points in the complex plane
- Define a grid of points in the complex plane
Iterative Mapping:
For each
Escape-Time Calculation:
Track the number of iterations
Assign a colour to
Edge Cases:
Points where
Points that remain bounded (
Pseudo-Code for Escape-Time Algorithm
# Input Parameters:
# - grid_size: Number of points in the complex plane grid.
# - max_iter: Maximum number of iterations.
# - R: Escape radius.
# - c, λ: Complex parameters.
# - p, q: Integers controlling the dynamics.
Initialize grid_points = [x + yi for x, y in complex plane range]
Initialize fractal_image = empty array of size [grid_size, grid_size]
for each point z_0 in grid_points:
z = z_0
for n = 1 to max_iter:
if |z| > R:
fractal_image[z_0] = color_based_on(n)
break
else:
z = z^q + c + λ / z^p
if |z| <= R after max_iter:
fractal_image[z_0] = black # Belongs to the Julia set
Display fractal_imageSynchronization of Julia Sets
Synchronization of Julia sets refers to the fascinating interplay between two distinct dynamical systems, where their fractal structures and trajectories align under specific control conditions. This phenomenon arises in the study of coupled systems, particularly in complex dynamics, where multiple Julia sets, associated with different parameters, exhibit coordinated behavior. Synchronization involves aligning the trajectories and fractal properties of two systems:
Driving System:
Response System:
Synchronization is achieved when the trajectory difference:
Coupling Mechanism
The response system incorporates a coupling term to align its dynamics with the driving system:
where
Why Synchronization Works
Synchronization is feasible because:
Both systems originate from the same functional framework.
Differences are limited to parameter variations (
The coupling mechanism effectively bridges the gap created by these parameter differences, aligning the trajectories and fractal properties.
Now, we’re introducing an additional control parameter
The equation provided is:
where:
a modified version of a Julia set generated by introducing a control mechanism into the dynamics of a rational map. This mechanism alters the behavior of the system, enabling adjustments to its fractal properties based on a coupling or control parameter
Base Map Contribution:
forms the unperturbed Julia set, as seen in System (2).
Secondary Influence:
introduces a coupling between the
Control Mechanism: The term:
applies feedback that synchronizes the
Mathematical Interpretation
This system describes a coupled rational map with feedback control, where:
Coupling: The term involving
Feedback: The parameter
Algorithm to Generate Controlled Julia Sets of System (5)
Key Components
Primary System (
This is the baseline iteration for Julia sets.
Secondary System (
Represents a synchronized auxiliary system.
Feedback Control:
Introduces controlled synchronization between
Steps
Initialize the Complex Grid:
Define the range of the complex plane (
Create a meshgrid for both
Iterative Process:
For each point on the grid, iterate
Use the control parameter
Escape Condition:
- Determine escape times based on the modulus (
- Determine escape times based on the modulus (
Visualization:
- Map the escape times to a color palette (e.g., viridis or inferno).
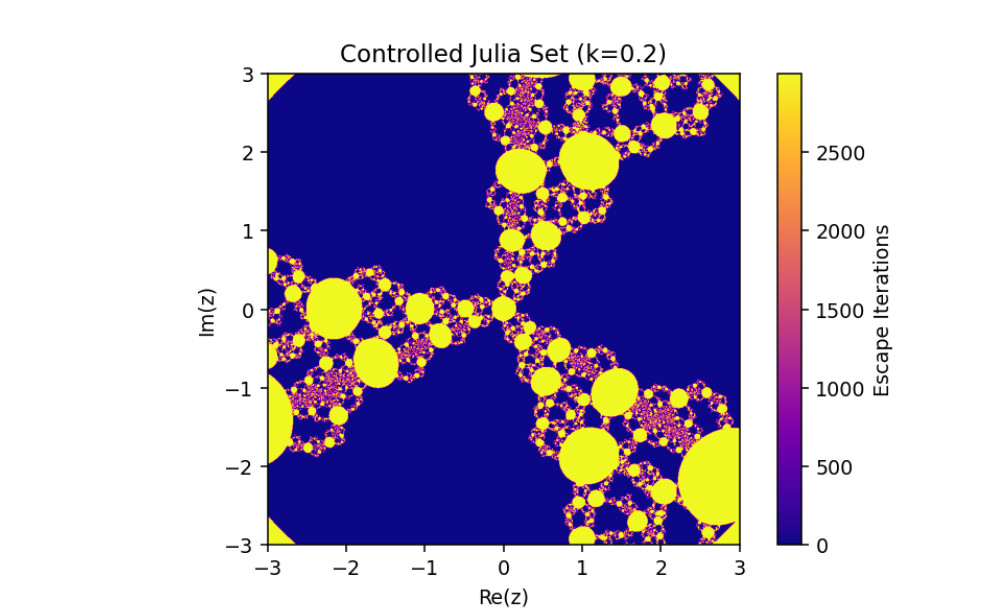
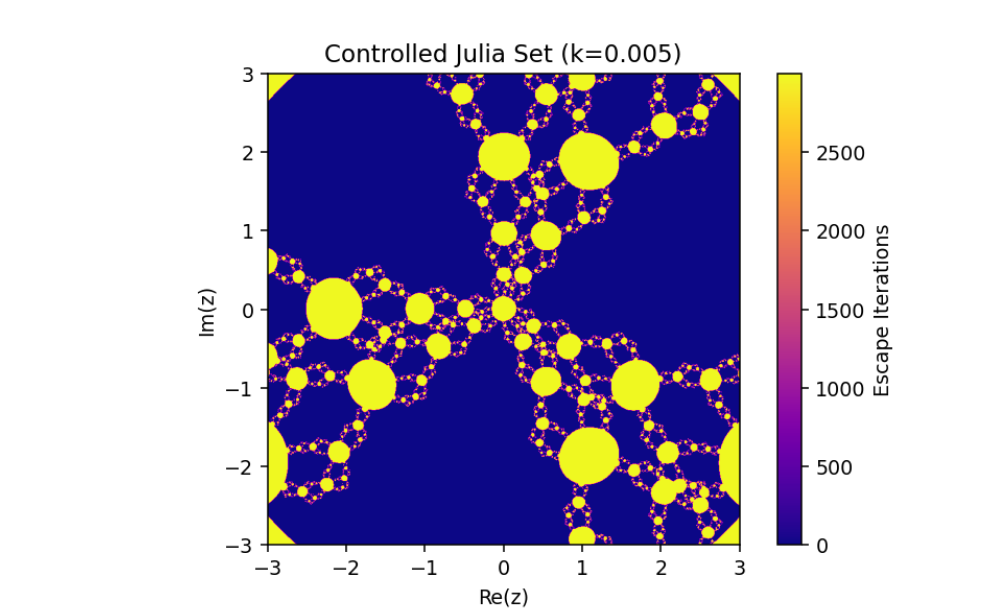
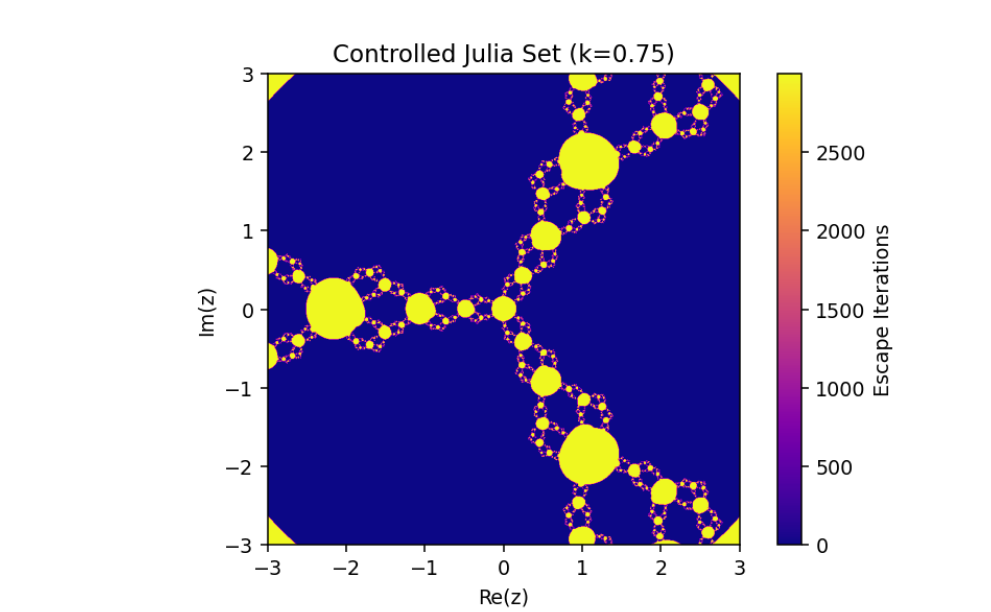
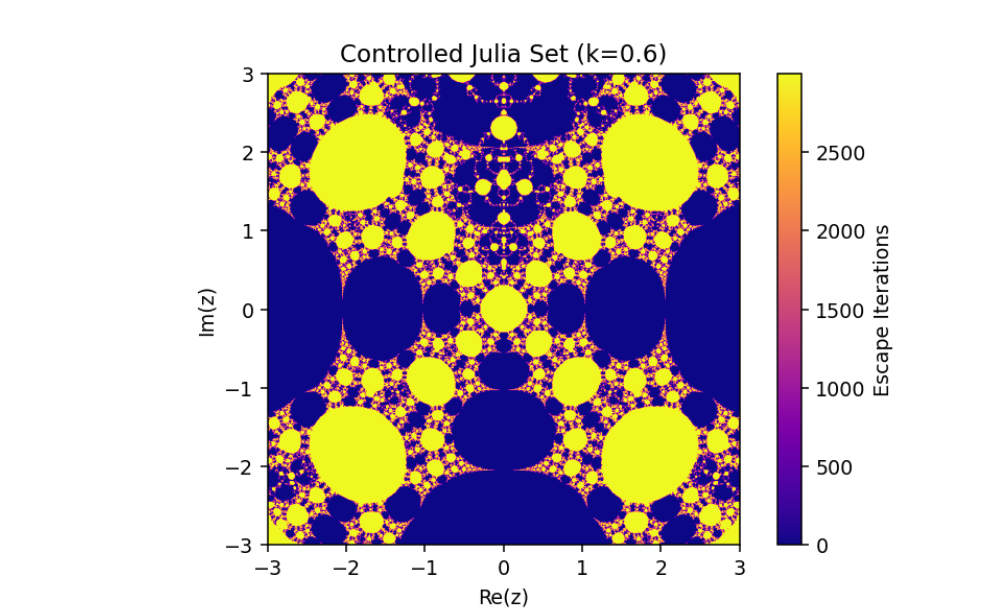
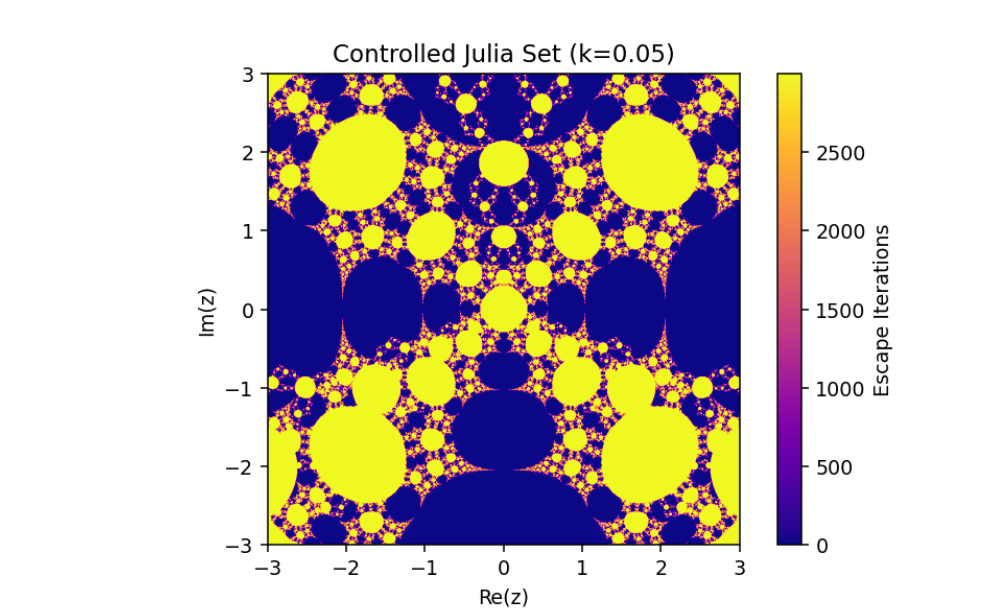
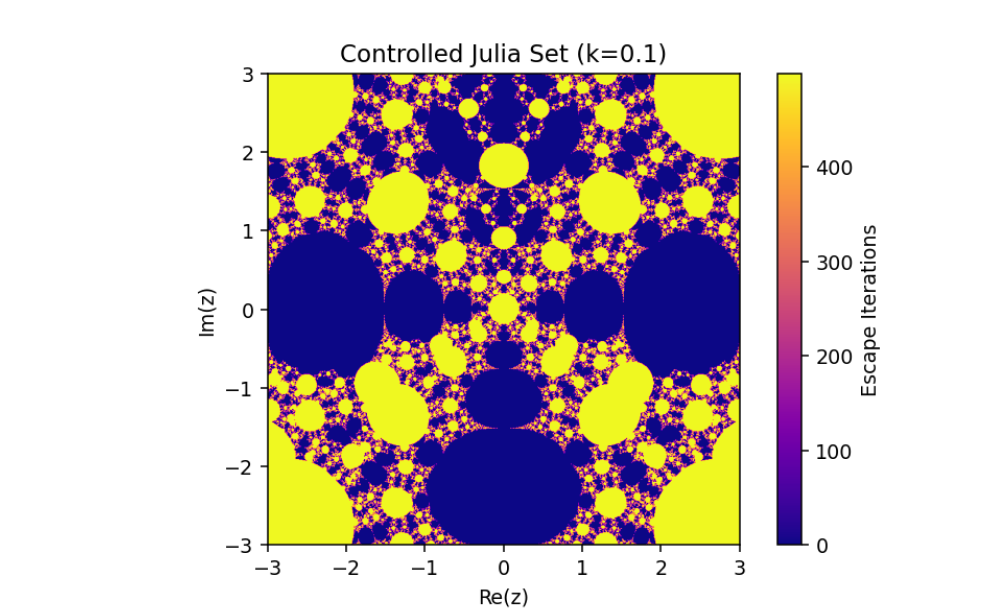
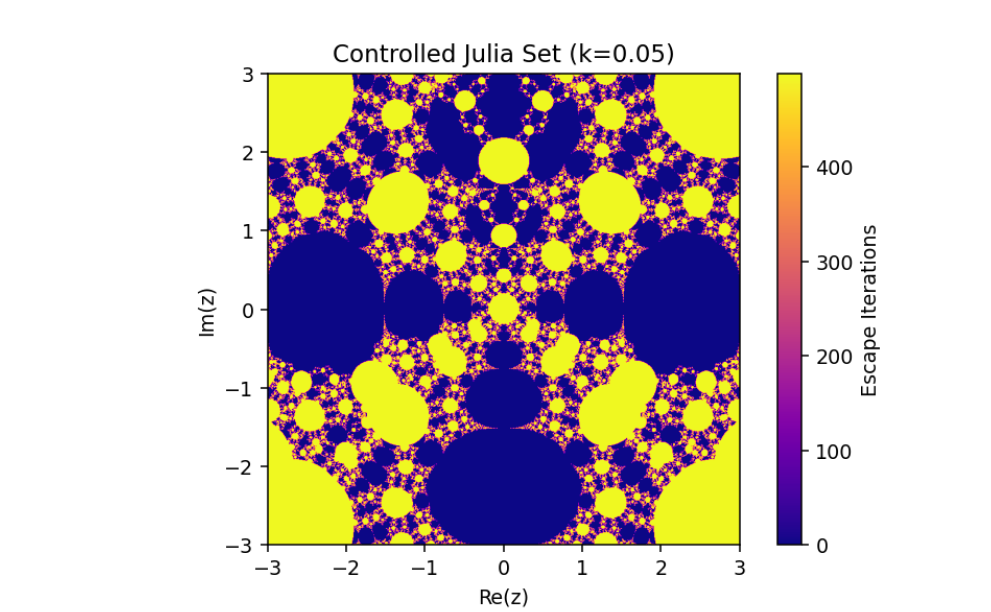
Controlled System (5) when
The changing of Julia sets of the controlled system (5) when
This emphasizes the critical role of feedback control in manipulating complex dynamical systems and offers valuable insights into the sensitive dependence of fractal geometries on system parameters.
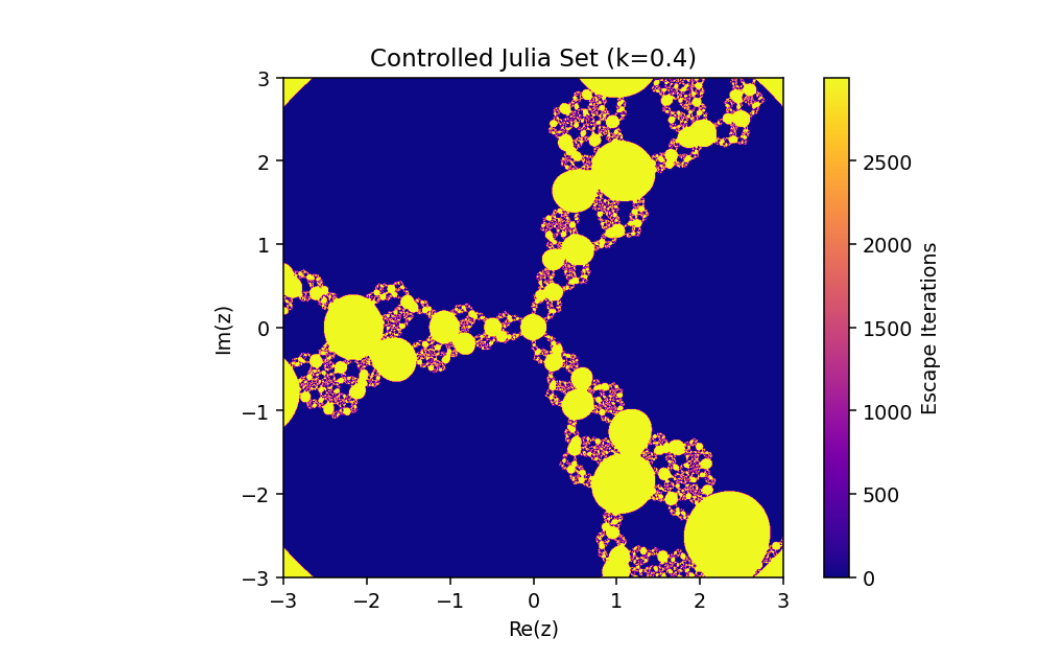
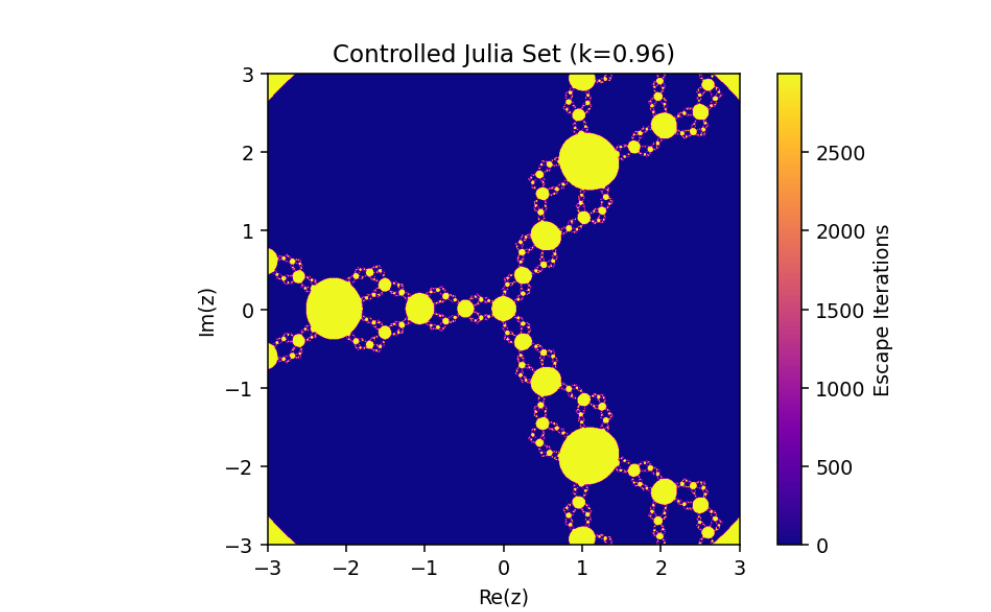
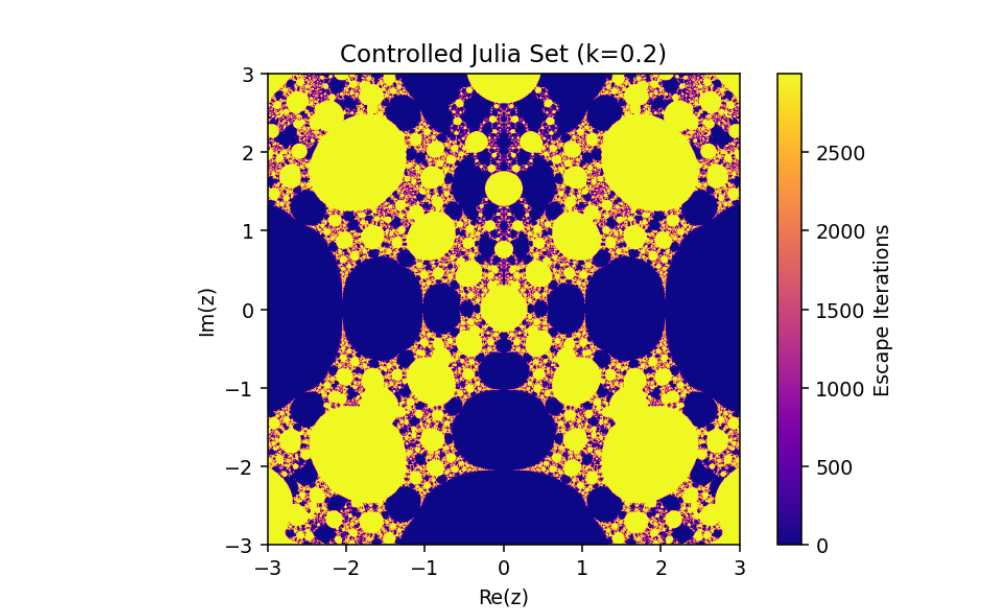
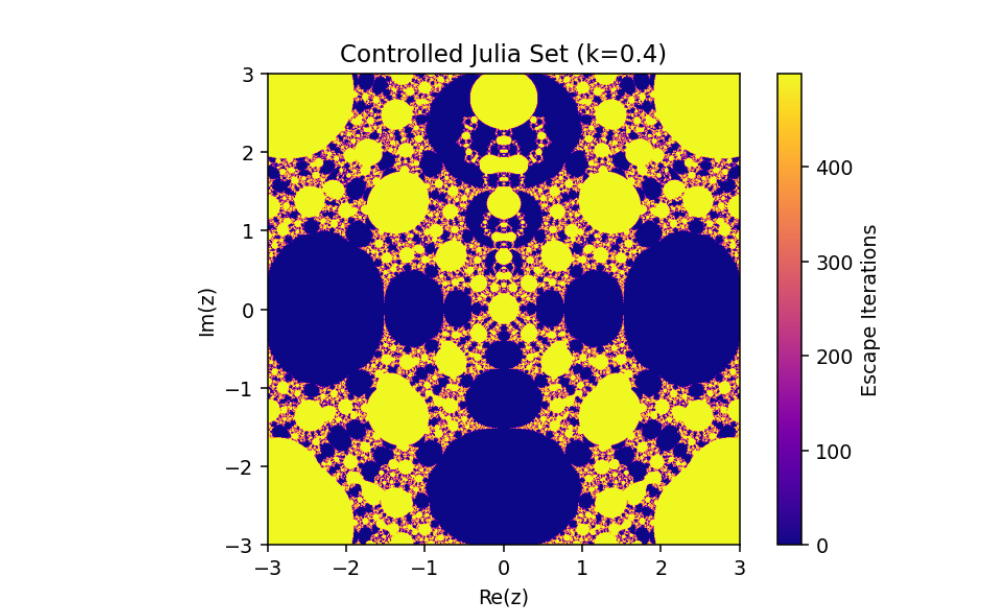
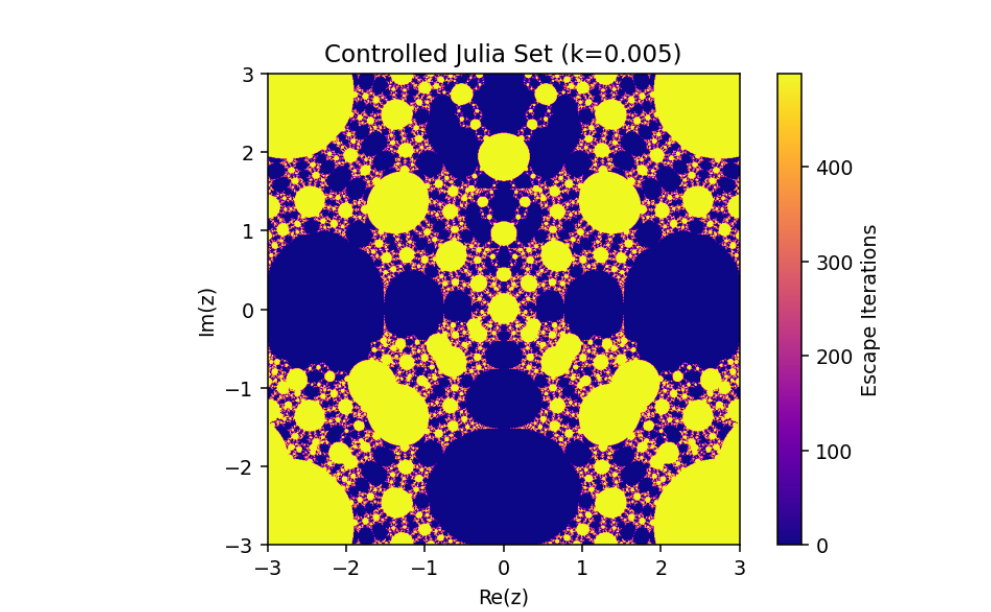
Controlled System (5) when
The changing of julia sets of the controlled system (5)
This variation emphasizes the sensitivity of the controlled system to specific parameter configurations, resulting in rich, intricate transformations of the Julia sets. These visualizations reveal the complex yet orderly nature of controlled dynamical systems, where stability and chaos coexist in fascinating patterns.
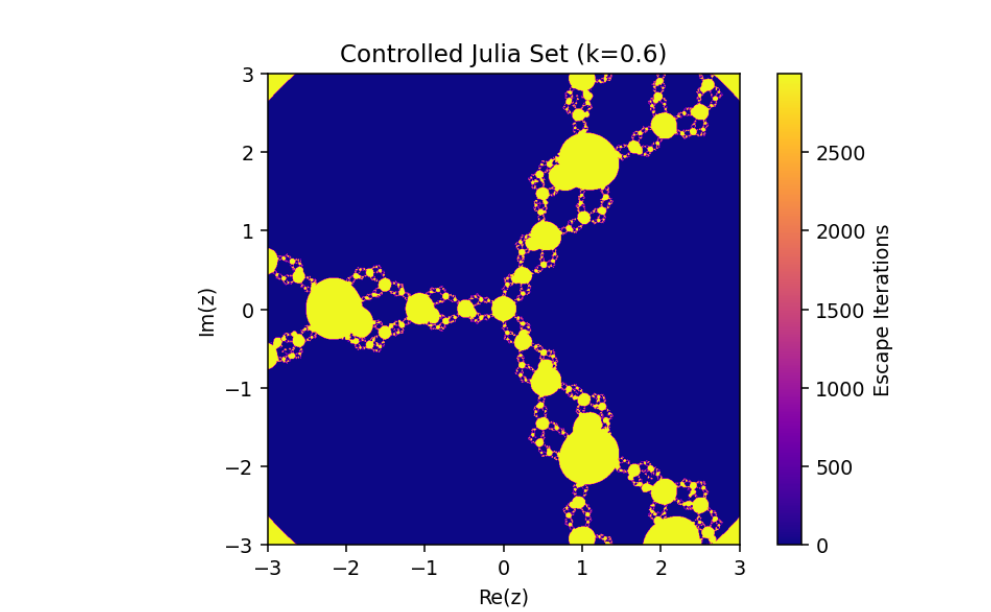
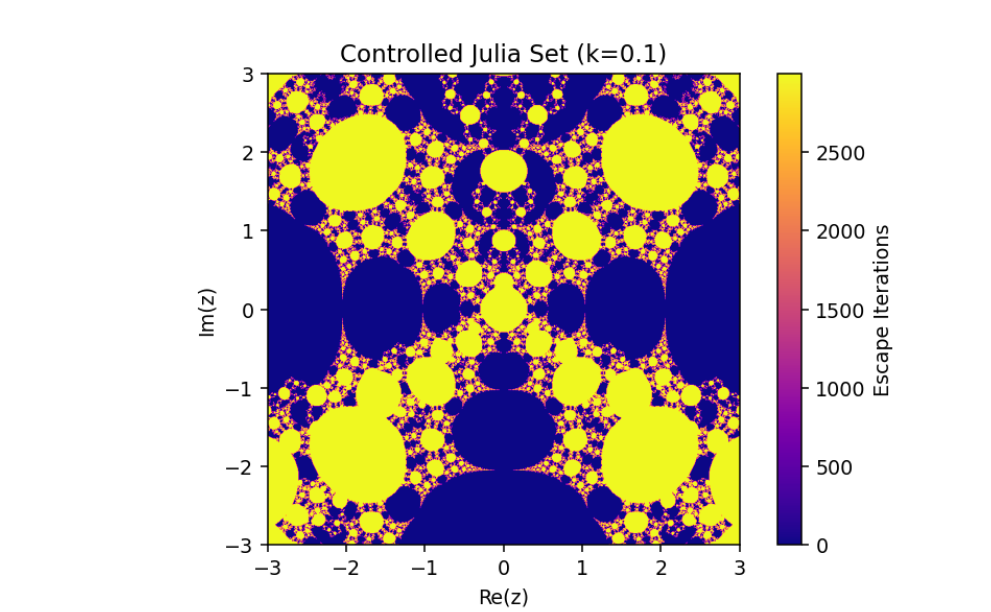
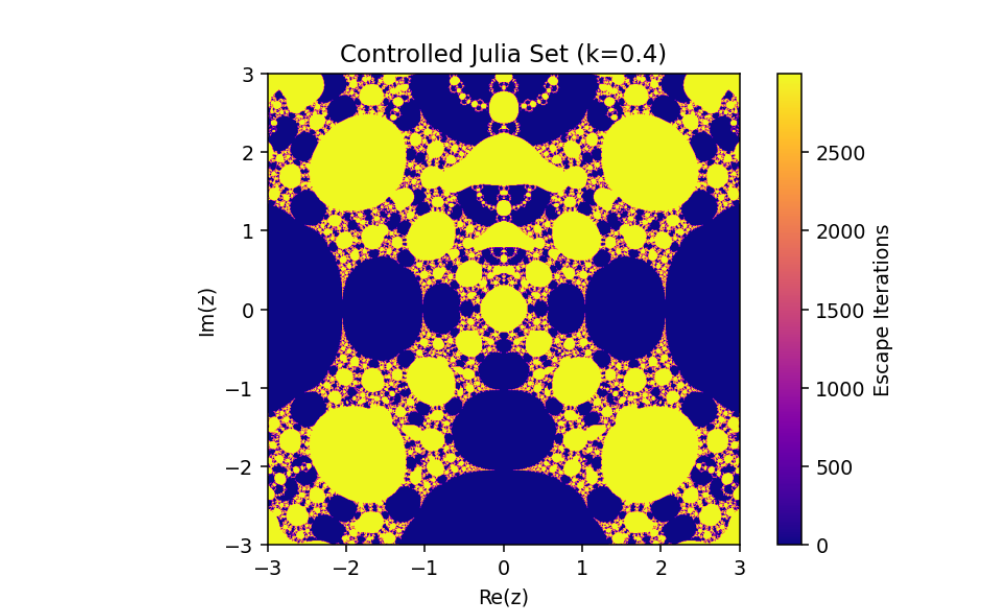
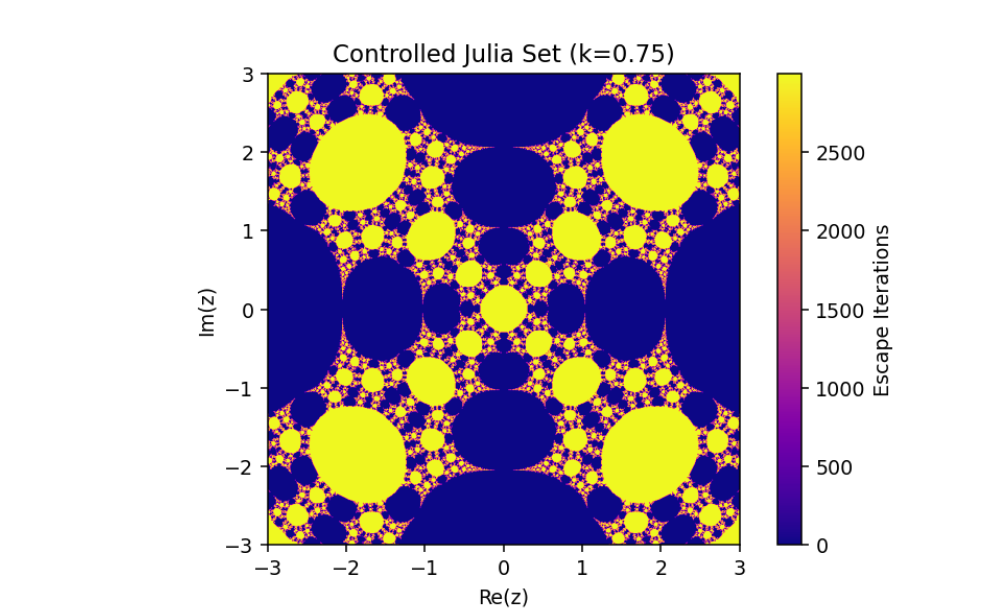
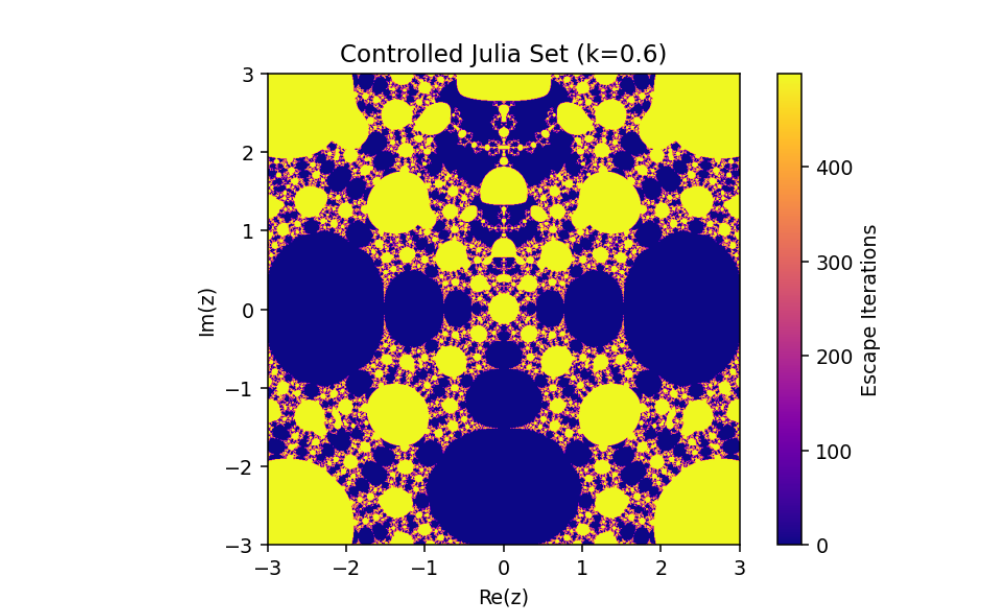
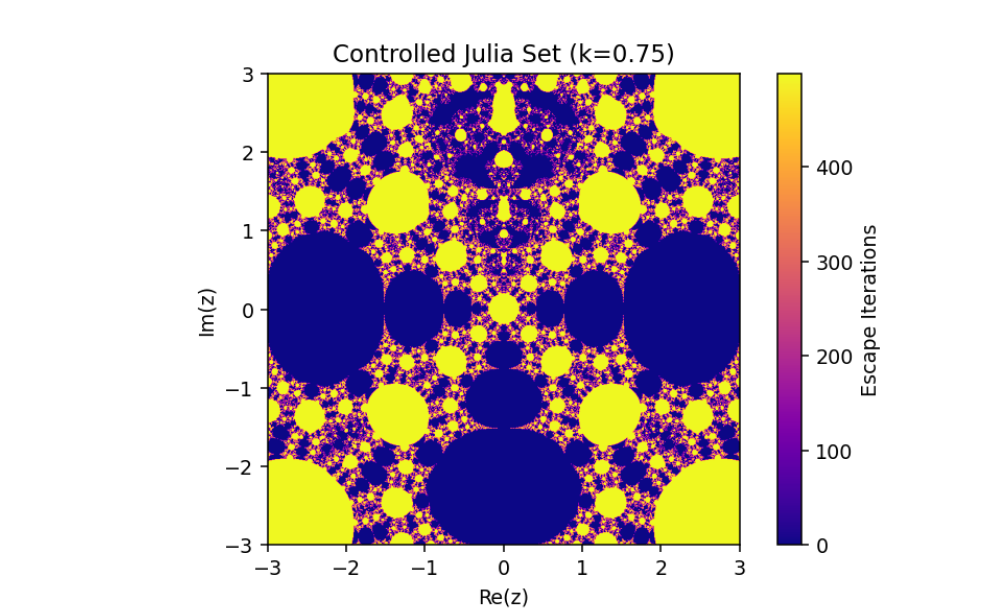
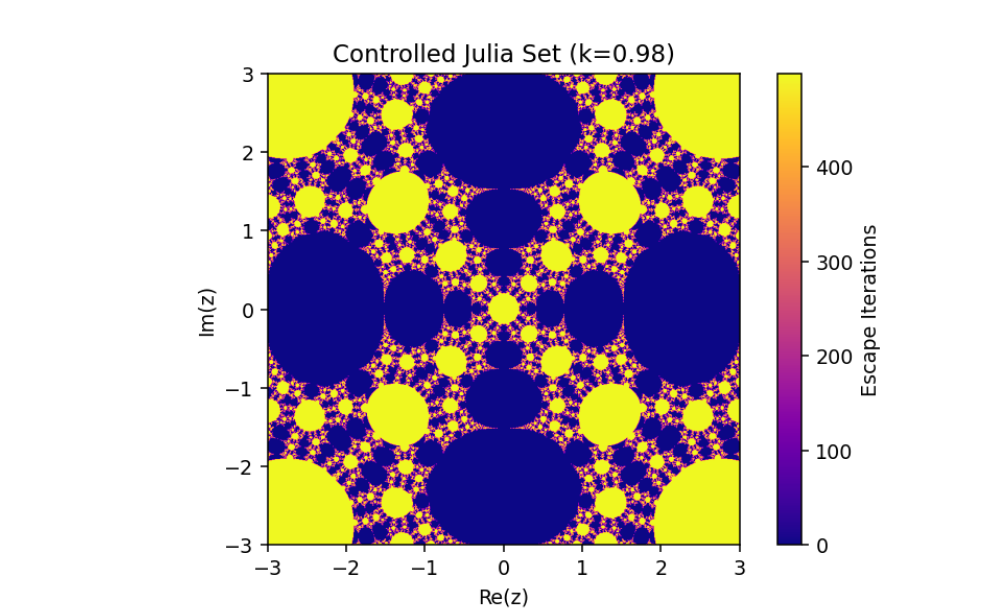
Controlled System (5) when
The exploration of the control system
This combination of parameters highlights the nuanced transitions between stability and chaos in the system, offering deeper insights into the fractal structures and their dependence on the controlled feedback. Such visualizations exemplify the delicate balance between system parameters in driving complex, visually striking dynamics.
Conclusion
In this paper, we have discussed the control and synchronization of Julia sets of the complex perturbed rational maps
Code References
See the Github Repository Fractal & Research
References
Amritkar, R. E. & Gupte, N. [1993] “Synchronization of chaotic orbits: The effect of a finite time step,” Phys. Rev. E 47, 3889–3895.
Carleson, L. C. & Gamelin, T. W. [1993] Complex Dynamics (Springer-Verlag, NY).
Beck, C. [1999] “Physical meaning for Mandelbrot and Julia sets,” Physica D 125, 171–182.
Zhang, Y. & Sun, W. [2011] “Synchronization and coupling of Mandelbrot sets,” Nonlin. Dyn. 64, 59–63.
Zhang, Y., Sun, W. & Liu, C. [2010] “Control and synchronization of second Julia sets,” Chin. Phys. B 19, 050512.
Kocarev, L. & Parlitz, U. [1996] “Synchronizing spatiotemporal chaos in coupled nonlinear oscillators,” Phys. Rev. Lett. 77, 2206–2209.