In our generation, we have turned psychology into a game of guesswork and probability. Forgetting that you must first know your mental power before wanting to predict the minds of others.
Motivation
On the \(18^{\text{th}}\) of August, \(1913\), crowds were going wild at the Monte Carlo Casino in Monaco. For the last \(10\) spins of the roulette table, the ball had landed on black. Thinking that surely the next spin will be red, gamblers from all over the casino started to pile their money on red. With every turn of the wheel, the crowd became more and more convinced that the next turn would be red. They increased their bets and their losses as black came up another \(16\) times, making a total streak of \(26\) blacks in a row. The chances of this happening are around one in \(66\) million. The casino made a fortune and the gamblers lost millions in francs, all because they fell prey to The Gambler’s Fallacy.
If you were at the Monte Carlo Casino that day, what would you have bet on? Red or black?
How It All Started
An account of the gambler’s fallacy was first published by the French polymath Marquis de Laplace in 1820. In A Philosophical Essay on Probabilities, Laplace noticed that men who wanted sons thought that each birth of a boy would increase the likelihood of their next child being a girl. Beliefs that resembled gambler’s fallacy were first seen in experimental settings during the 1960s when researchers were exploring how the mind makes decisions using probabilities. In these experiments, subjects were asked to guess which of two colored lights would light up next. After seeing a succession of one color being illuminated, researchers noticed that subjects were much more likely to guess the other.
In this article, we are going to see exactly where the gamblers went wrong and how, with the right thinking, they could have avoided their staggering losses. It’s subtler than you might think.
A Classic Chance Process
Random Experiment: Coin Flip
To illustrate the concepts, we are going to consider a classic chance process (or chance experiment) of flipping a coin. You know that when you flip a coin, there’s a half chance it’ll land on heads and a half chance it’ll land on tails.
So, let’s say you’re flipping a coin with someone, and the first time you flip it is head, the next time you flip it is head again, again you flip it is head, once more time you flip the coin you might be tempting to think that the chances of tails are higher this time, that a tail is due.
The chances of \(4\) heads in a row are \(\frac{1}{16}\) or \(6.25\%.\)
If you thought this, you just fell prey to the gambler’s fallacy, the false belief that independent past events can affect the likelihood of independent future events in the same random experiment. The coin has no memory of its last three flips. The chances of getting a head or a tail on the next flip are still \(\frac{1}{2}.\)
In gambling culture, there’s an adage.”The dice have no memory.”
The probability of \(3\) heads in a row and then a tail is also \(\frac{1}{16}.\) Now, you see that the last time you flipped the coin it is head, didn’t plan this to make a point, by the way. We see this same faulty reasoning every time you hear someone say, “Well, you’ve had three boys, so the next one must be a girl”. The chance of having a girl is still around \(50/50.\)
Statistical Independence
Coin flips and childbirth is what’s called statistically independent. Each occurrence is independent of previous and future occurrences. We tend to think of chances as self-correcting, or that there must be a cosmic balancing out. Because there was a streak of black balls, this needs to be balanced out by some red balls. The gambler’s fallacy comes from the fact that we expect statistically independent events to influence each other, to balance each other out when they don’t.
Now, if that were the end of the story, this would be pretty boring. This belief in a cosmic balancing out isn’t as silly as it sounds. If we flip this coin for long enough, we’d start to see something very interesting. Now, it’s quite obvious that nobody has to sit around all day flipping coins, but you should know of someone who did so.
Mathematician J.E.Kerrich’s Experiment
Begging of Law of Large Number
In 1939, a South African mathematician named J.E. Kerrich took an ill-advised trip to Europe. Long story short, he ended up in an internment camp in Denmark. Out of curiosity or pure boredom, he flipped a coin \(10,000\) times and recorded the number of times it landed on head. His result looked like this.
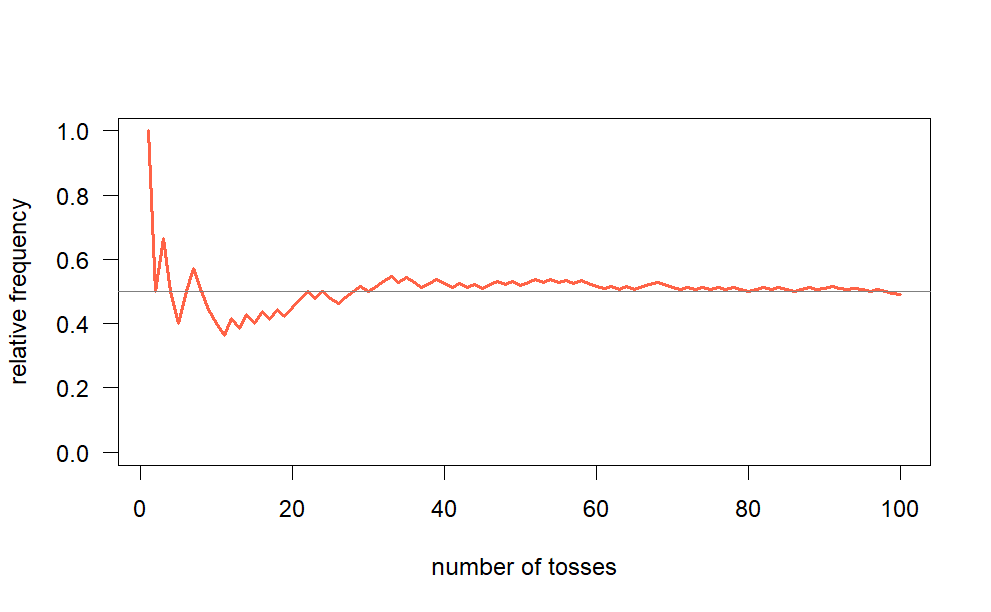
The more times J.E. Kerrich flipped the coin, the number of times he flipped a head, or in statistics talk, the relative frequency of heads, got closer and closer to \(50\%.\) Kerrich only had enough time to do one lot of \(10,000\) flips, but here are some computer simulations of his same experiment. Every time we see
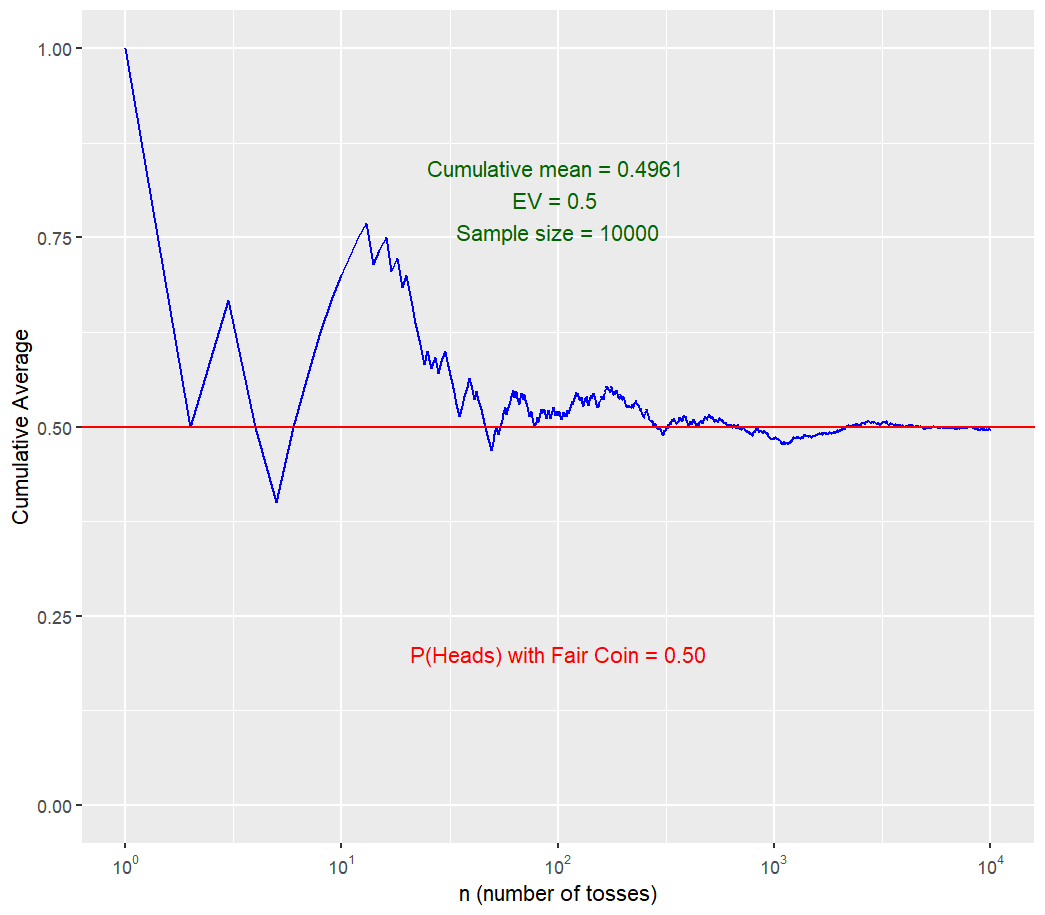
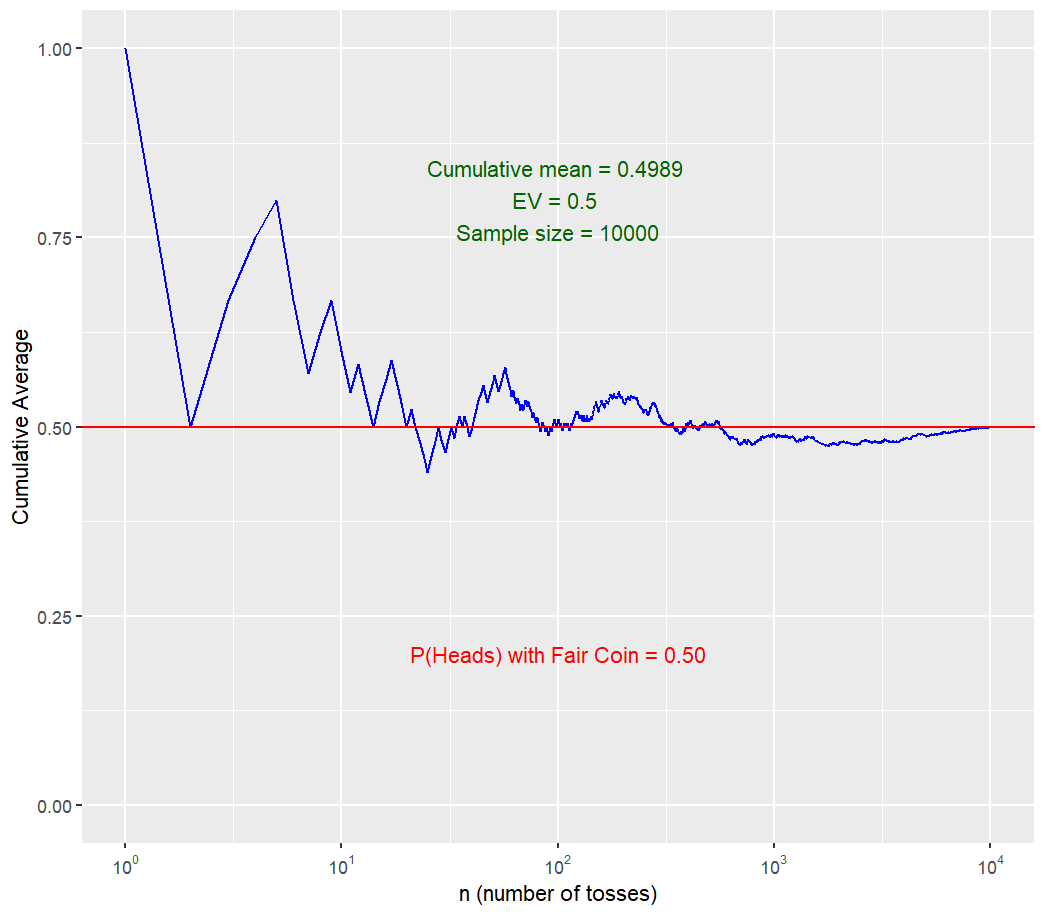
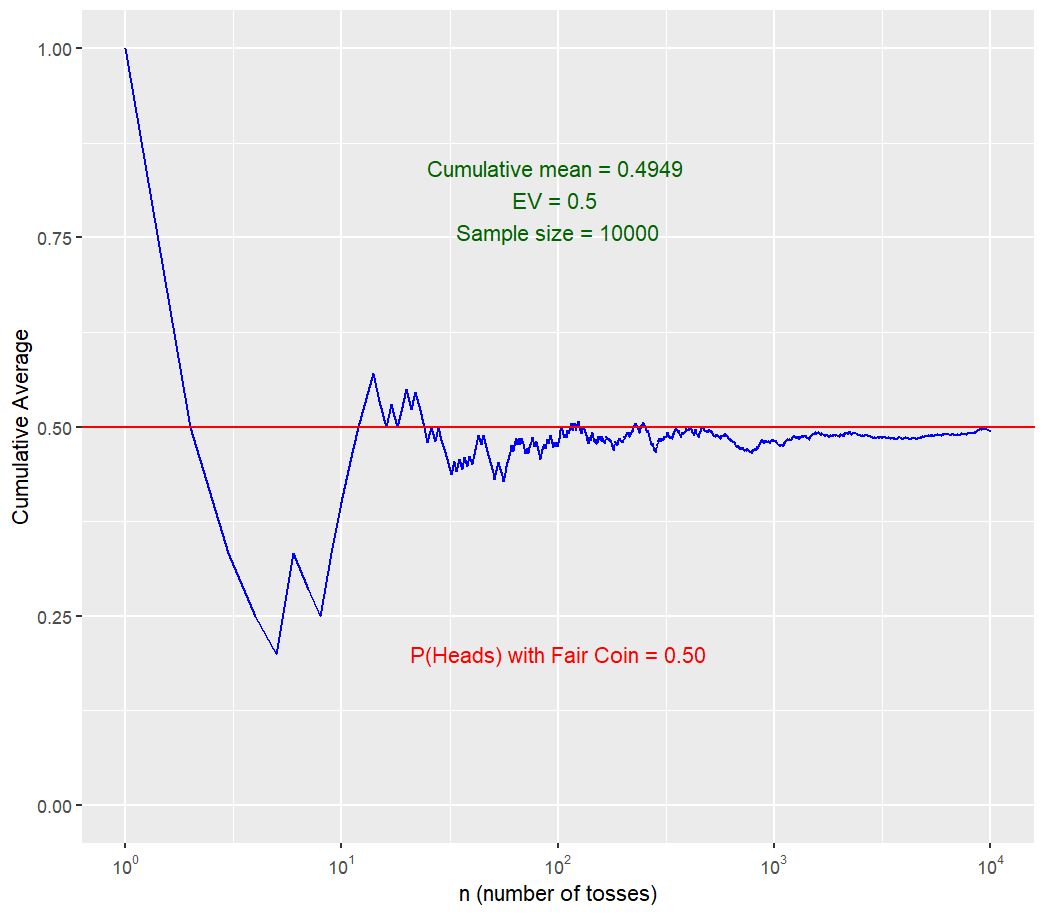
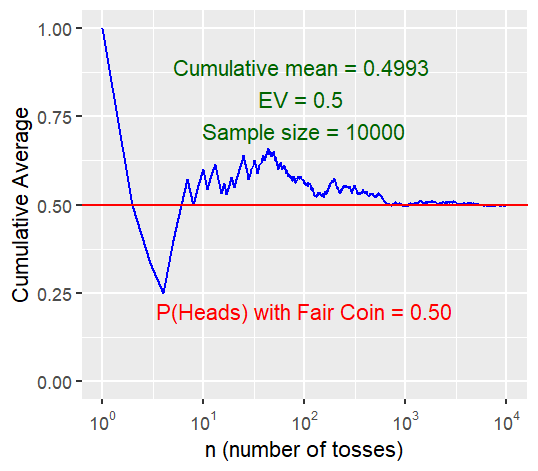
the same pattern. The relative frequency of heads (Here, the Cumulative Percentage of Heads is computed) flipped always ends up being around \(50\%.\) This isn’t a feature of coins. With a dice, the chances of it landing on each face are \(\frac{1}{6}\) or \(16.67\%.\) Here’s the
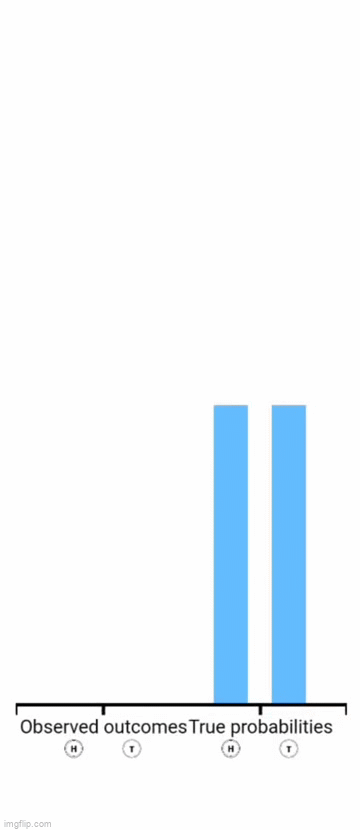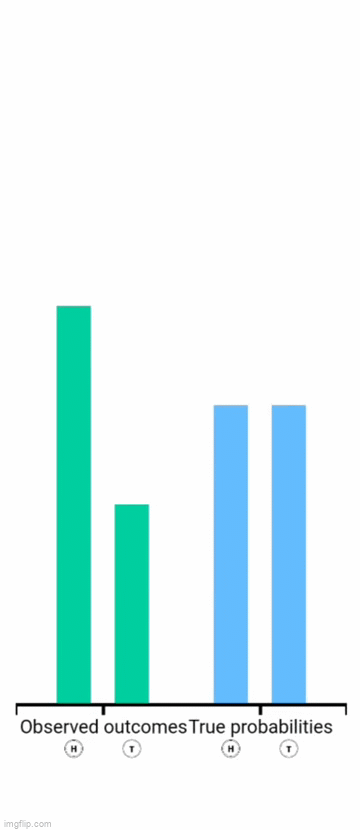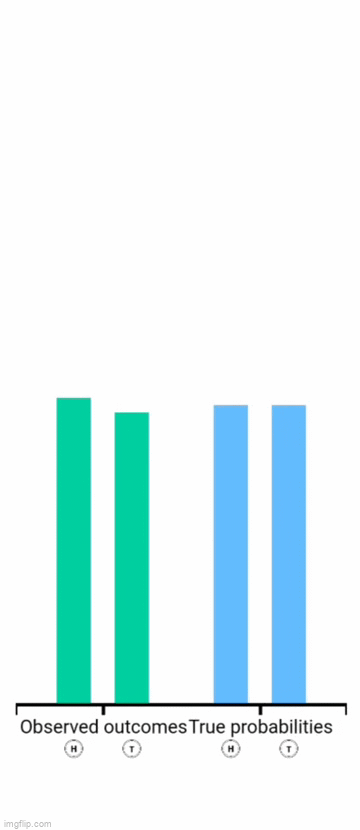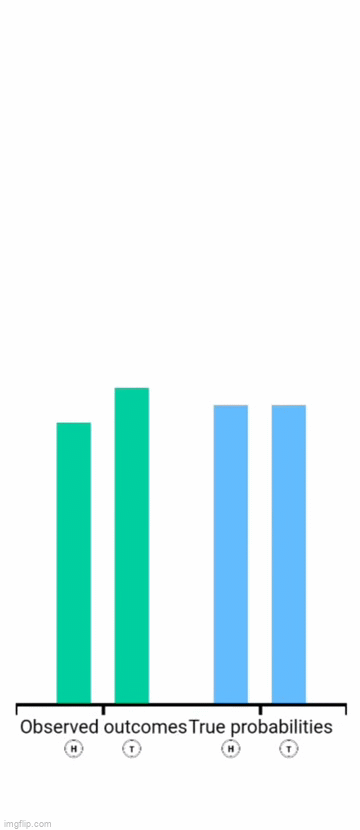
Perform this simulation https://seeing-theory.brown.edu/basic-probability/index.html
Computer simulation of \(10,000\) rolls of a dice. The more rolls we make, the green histogram will closer and closer to the blue histogram i.e., the relative frequency of each faces gets closer and closer to \(16.67\%.\) This phenomenon is called the Law of Large Numbers. The more rolls, flips, or trials we do, the closer the relative frequency of the outcome approaches the probability of the event.
The probability of heads coming up in a single flip is \(50\%,\) and after enough flips, the relative frequency of heads flipped is about \(50\%.\) The probability of rolling a \(3\) on a die is \(16.67\%\), and after enough rolls \(3\) shows up very close to \(16.67\%\) of the time.
Reconcile Seemingly Paradoxical Ideas
Uniformity and Balancing out
This kind of makes it seems to like chance is self-correcting, that there is some sort of cosmic balancing out. So, on one hand, we have statistical independence, which tells us that each turn is completely unrelated to the last and the gamblers were mistaken to think that past results would affect future results. But on the other hand, we have the law of large numbers, which tells us that systems of chance do eventually balance out. So, it would seem that gamblers were right to expect that a red was due after a long streak of black.
So how can we reconcile these two seemingly paradoxical ideas?
Contrary to popular belief, size does matter. It’s called the law of large numbers for a reason. We only see this uniformity, or balancing out, after a large number of trials. Small sample sizes often show extreme variability. It’s much more likely to see \(9\) heads in a row than \(99\) in a row.
Bill & Melinda Gates Foundation’s Study
One of the most famous examples of this phenomenon comes from a study done by Bill & Melinda Gates Foundation. The foundation studied educational outcomes in schools and found that small schools were always at the top of the list, inferring that small schools lead to better education. The foundation applied small school techniques to larger schools, like decreasing class sizes and lowering the student-teacher ratio. But these techniques failed to produce the dramatic gains they were hoping for.
99 Average-sized school
100 Large school
101 Small school
102 Small school
103 Small School
One crucial thing the foundation overlooked was that the schools at the bottom of the list were also small schools. It wasn’t that small schools perform better, but smaller schools have more variable test scores. A few child prodigies can skew small schools’ averages up significantly while a few slackers can skew it down significantly. In a large school, a few extreme scores will just dissolve into a big average, max to max budging the overall number. We can take it a step further and talk about small sample sizes within large sample sizes. You can bet that in Kerrich’s \(10,000\) coin flips, he would’ve seen some long streaks of tails and some long streaks of heads which would’ve just ended up dissolving into the big average.
What Does Chance Ever Do For Us
Suppose, there is a family with \(5\) girls. If this family had another 1,000 children, we’d see a more even split of boys and girls. Though there would still be some streaks of girls in a row and some streaks of boys in a row. And the 26 blacks at the roulette table were just a relatively short streak in a series of millions of spins. To quote the late astronomer, Carl Sagan,
“Randomness is clumpy.”
The mistake the gamblers made was treating small sample sizes the same as large sample sizes when they couldn’t be more different. Although it wasn’t completely unreasonable for gamblers to bet on red after such a long streak of black, it was still the wrong move because their sample size was too small to obey the law of large numbers. The cognitive mistake of treating small sample sizes the same as large sample sizes are ironically called the law of small numbers, and it works the other way around too. Sometimes we wrongly infer things about a whole population from a small sample of it.
If you caught \(10\) fish, \(7\) of which had gross boils on them, you might infer that \(70\%\) of the entire population of that time of fish has gross boils on them. But that would be a mistake because the small sample sizes are not representative of their larger population.
Now that we know some of the reasons behind the gambler’s fallacy, it’s interesting to ask: Why do we make these mistakes? , Why do we equate smaller sample sizes with larger ones when they’re different?
Representativeness Heuristic
Mental Shortcut
Psychologists Amos Tversky and Daniel Kahnemann have proposed it’s due to a very strong cognitive bias called the ‘Representativeness Heuristic’. A heuristic is a kind of mental shortcut that allows people to solve problems and make judgments quickly and efficiently. These rule-of-thumb strategies shorten decision-making time and allow people to function without constantly stopping to think about their next course of action. However, there are both benefits and drawbacks of heuristics. While heuristics are helpful in many situations, they can also lead to cognitive biases. Becoming aware of this might help you make better and more accurate decisions.
The representativeness heuristic involves estimating the likelihood of an event by comparing it to an existing prototype that already exists in our minds. This prototype is what we think is the most relevant or typical example of a particular event or object. The problem with this is that people often overestimate the similarity between the two things they are comparing.
Making decisions based on representativeness involves comparing an object or situation to the schemas, or mental prototypes, that we already have in mind. Such schemas are based on past learning, but can also change as a result of new learning. If an existing schema doesn’t adequately account for the current situation, it can lead to poor judgments. When we make decisions based on representativeness, we may be likely to make more errors by overestimating the similarity of a situation. Just because an event or object is representative does not mean that what we’ve experienced before is likely to happen again.
Heuristics Leads to Astray
They’re deeply ingrained in us and they helped our species survive. Imagine you are on a jungle safari and suddenly you’re in front of an animal you’ve never seen before. Taking one look at it, would you run or try to pat it? You’ve probably answered run, and that’s a smart decision. Even though you don’t know for sure if it’s dangerous, it looks very similar to other animals you do know are dangerous. It has sharp teeth, like a bear, eight legs like a poisonous spider, and sharp claws, like a lion. This particular type of mental shortcut, or heuristic, is a representativeness heuristic. This animal is representative of other dangerous animals so you lump it in the same category. But heuristics can also lead us astray.
According to Amos Tversky and Daniel Kahnemann, the gambler’s fallacy is an example of this same heuristic leading us astray. We expect our current experiences to be representative of our past experiences. Most families we’ve encountered have a pretty even split of boys and girls, so we expect that all families we encounter will have a pretty even split of boys and girls. Most of the time we’ve encountered random processes, like a roulette wheel, and we’ve seen a pretty even spread of the available outcomes. For example, black and red spins. So when we see a long streak of blacks in a row, we expect some reds will come along to balance it out because that matches our previous experience.
Effectiveness of Gambler’s Fallacy
The Gambler’s Fallacy can lead to suboptimal decision-making. Part of making an informed decision surrounding a future event is considering the causal relationship it has with past events. In other words, we connect events that have happened in the past to events that will happen in the future. They are seen as causes or indications of how the future will unravel.
This is a good practice when the two events are indeed causally related. For instance, when we notice storm clouds in the sky, it is reasonable to assume that it will rain, and then decide to pack an umbrella. Past experience dictates that storm clouds are good indicators of rain because they are causally related.
But this can be problematic when two events are not causally related but we think they are. This is because we are basing our decisions surrounding a future event on false information. What follows is a probabilistic outlook that is off the mark, and an ignorance to the true causes of the event. Think of an investor that takes her successful track record as an indicator for the likelihood of her future investment being a success. The two aren’t necessarily causally related. As a result of mistakenly thinking that the future will imitate the past, she might overestimate the probability of success and not fully scrutinize her assets for true indicators of their future worth.
Conclusion
Gambler’s fallacy doesn’t just affect those of us who go to casinos — that much should be clear by now. It can affect any of us when we are assessing the probability of a future event by looking at past events that are similar. We do this all the time in both our personal and professional lives. It is easy to make the mistake of doing this with events that are causally independent, which can mess up our predictions surrounding probability and the decisions that follow from them. We don’t want to misidentify characteristics of past relationships as indicators that our current relationships will necessarily follow that path. Nor do we want to look at a string of job rejections as a sign that we won’t find a job in the future.
References
Ayton, P.; Fischer, I. (2004). “The hot-hand fallacy and the gambler’s fallacy: Two faces of subjective randomness?”. Memory and Cognition. 32 (8): 1369–1378. doi:10.3758/bf03206327. PMID 15900930.
Burns, Bruce D.; Corpus, Bryan (2004). “Randomness and inductions from streaks:”Gambler’s fallacy” versus “hot hand””. Psychonomic Bulletin & Review. 11 (1): 179–184.
Why we gamble like monkeys”. BBC.com. 2015-01-02.
Croson, R., & Sundali, J. (2005). The Gambler’s Fallacy and the Hot Hand: Empirical Data from Casinos. Journal of Risk and Uncertainty, 30(3), 195-209. doi:10.1007/s11166-005-1153-2
Barron, G., & Leider, S. (2010). The role of experience in the Gambler’s Fallacy. Journal of Behavioral Decision Making, 23(1), 117-129. doi:10.1002/bdm.676