“Once you’ve ruled out the impossible, whatever remains – however improbable – must be true” ~ Sherlock Holmes (The Adventure of Black Peter)
The Birth of Calculus
Paradox to Understand The Limit
Calculus was discovered in the middle of the \(1670\)s which was a breakthrough in mathematics. The word comes from Latin meaning small stones because it deals with problems where big thing needs to be broken down into lots of little things. Without it, humans would never have left our own planet. Engineers use it to determine how much material they need for a job or how much power they should give a motor. Biologists use it to determine the rate of disease spread and chemists use it to measure reactions.
But where did this magical tool come from?
Dichotomy Paradox
The earliest questions that calculus was invented to answer came in the form of paradoxes. In this episode of the article, we’re going to understand and explore a paradox that will help us to explore the very fundamental and important concept of calculus which is the backbone of mathematics.
This is Zeno of Elea, an ancient Greek philosopher famous for inventing a number of paradoxes, arguments that seem logical, but whose conclusion is absurd or contradictory. For more than \(2,000\) years, Zeno’s mind-bending riddles have inspired mathematicians and philosophers to better understand the nature of infinity. He had a strange but interesting view of the world. He thought that we couldn’t trust our senses but only logic and invented a paradox to demonstrate one of the best-known problem is called the ’dichotomy paradox’, which means, “the paradox of cutting in two” in ancient Greek. It goes something like this:
Towards Our Objective
After a long day sitting around thinking Zeno decides to walk from his house to the park. The fresh air clears his mind and helps something better. In order to get to the park he first has to get halfway to the park. So, \(t_1\) portion of the journey takes a finite amount of time. Once he gets to the halfway point, he needs to walk half the remaining distance. Again, \(t_2\) portion of the journey takes a finite amount of time. Once he gets there, he still needs to walk half the distance that’s left, which takes another finite amount of time. This happens again and again and again.
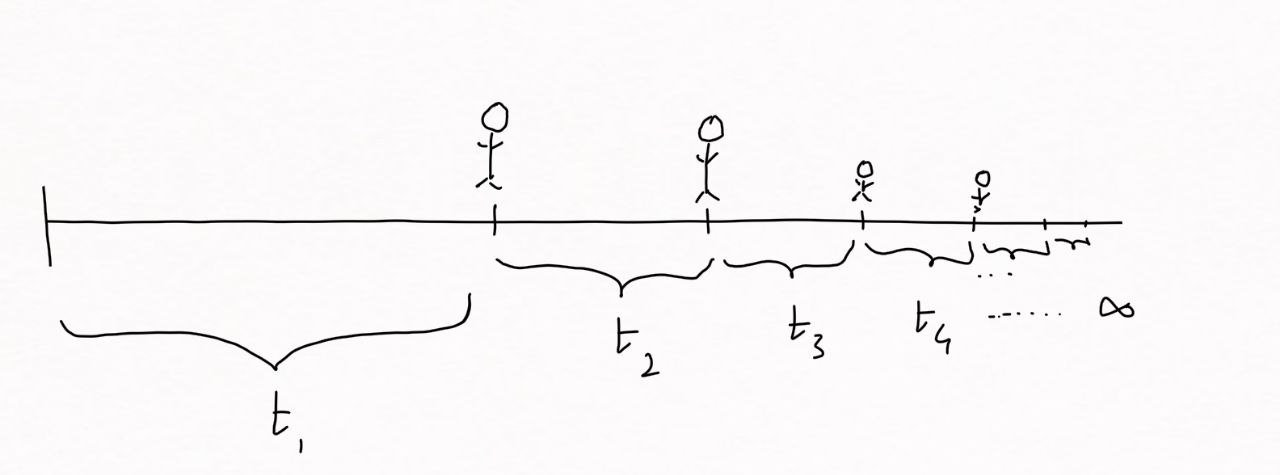
You can see that we can keep going like this forever, dividing whatever distance is left into smaller and smaller pieces, each of which takes some infinite time to traverse.
So, how long does it take Zeno to get to the park?
Well to find out, you need to add the times of each of the pieces of the journey. The problem is, that there are infinitely many of these finite-sized pieces.
So, shouldn’t the total time be infinite?
This argument is completely general. It says that traveling from any location to any other location should take an infinite amount of time. In other words, it says that all motion is impossible. This conclusion is totally absurd.
but where’s the flaw in the logic?
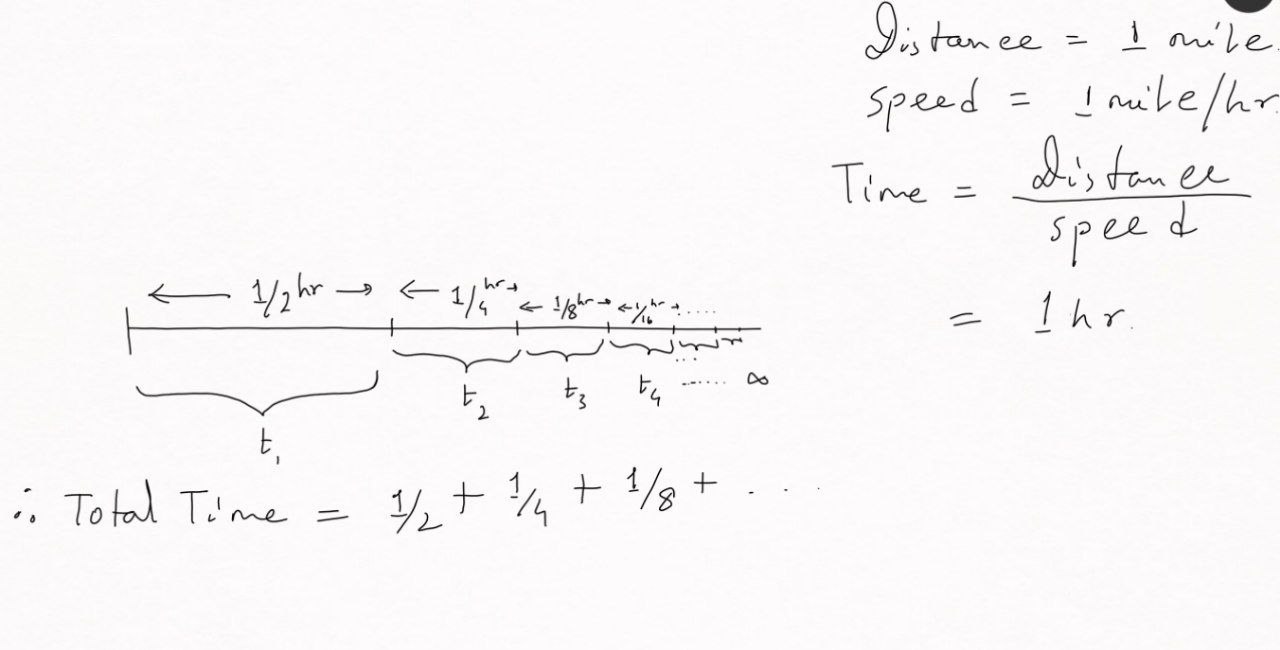
To resolve the paradox, it helps to turn the story into a math problem. Let’s assume that Zeno’s house is \(1\ mile\) from the park and that Zeno walks at \(1\ mile/hr\). Common sense tells us the time for the journey should be one \(1\). But, let’s look at things from Zeno’s point of view and divide up the journey into pieces. The first half of the journey takes \(\frac{1}{2}\ hour\), the next part takes a quarter of \(\frac{1}{2} \ hour\) i.e., \(\frac{1}{4} hour\) , the third part take \(\frac{1}{8}\ hour\) and so on. Summing up all these times, we get a series that looks like this.
\[\text{Total Time = }\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+ \frac{1}{16} + \ldots \]
Now, Zeno might say,
“since there are infinitely many terms on the right-hand side of the equation and each individual term is finite, the sum should equal to infinity right?”
This is the problem with Zeno’s argument. As, mathematicians have since realized, it is possible to add up infinitely many finite-sized terms and still get a finite answer. The numbers we’re adding on keep getting smaller but the sum never ends. There’s an infinite amount of fractions to add on. If a sum gets bigger every time you add on a fraction and you have an infinite amount of numbers to add on, shouldn’t the total distance get infinitely large? and if the distance is infinitely large surely you can never traverse it.
Development of Calculus
This was the early problems that led to the invention of a mathematical tool i.e., the backbone of calculus which is limit. Let’s take a closer look at how this sum breaks down. In the first two terms, add to get \(0.75\). Adding one more term gives us \(0.875\) and adding another gives \(0.9375\). The sum is just getting closer and closer to \(1\) and there doesn’t seem to be any risk of it running off to finish. Even though we have an infinite number of fractions to add they seem to be approaching the number \(1\). We might make it to our final destination after all, but how do we know for sure? No matter how many terms we add on to the sum by hand there will always be another one we can add on after that without actually ever reaching \(1\). It’s exactly this type of problem that the limit was created to deal with. To help us understand what the mathematical limit mean to us, let’s rewrite the problem. We’ve been writing out total distance as a sum like this
\(\displaystyle \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+ \frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256} + \ldots\) but it can be written much more conveniently like this.
\[S_n=1 -\frac{1}{2^n}\] And if you’re interested, the derivation is given below.
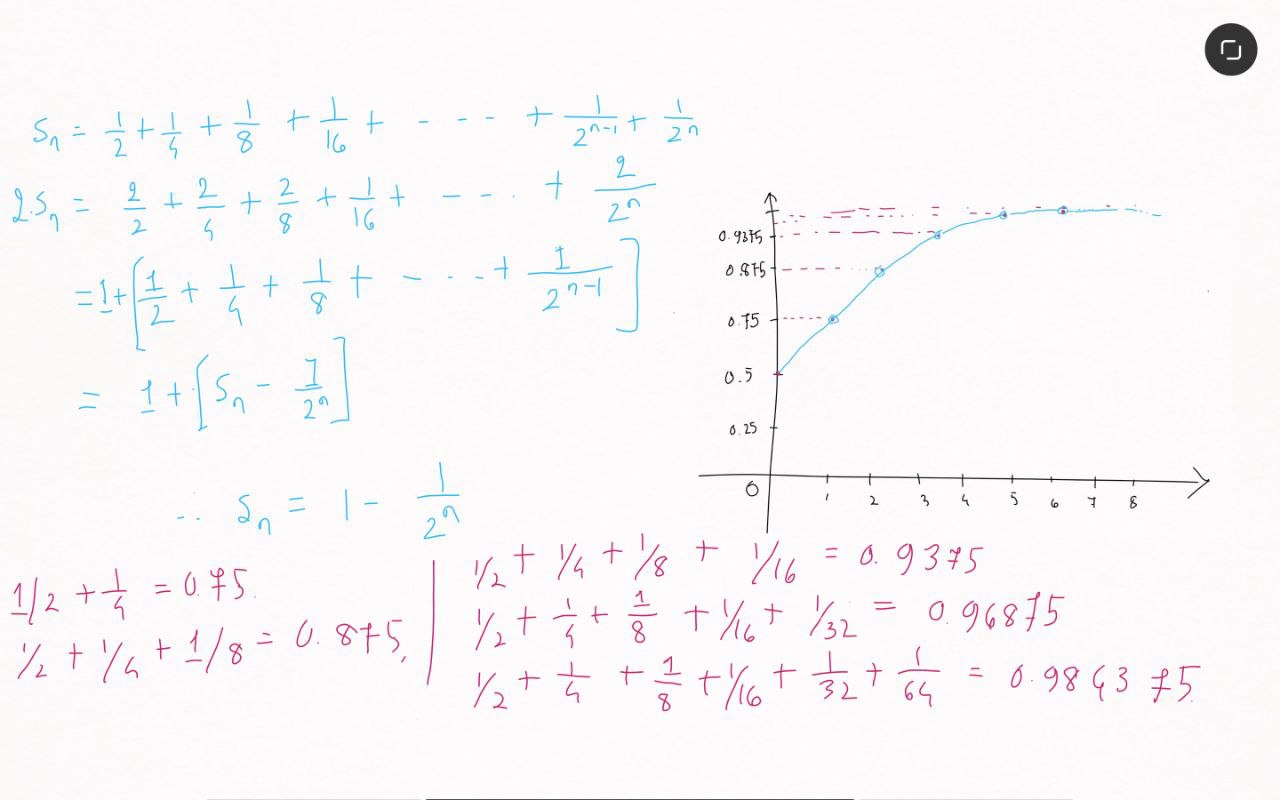
Written like this \(S_n = 1-\frac{1}{2^n}\), the term \(S_n\) and \(\frac{1}{2^n}\) is much easier to work with. Here, the \(n\) stands for the number of terms in our sum. The more terms there are, the larger \(n\) gets which means that this term here, \(2^n\) gets large. The bigger \(2^n\) gets, the smaller the \(\frac{1}{2^n}\) gets the close the sum gets to equaling \(1\). This logic is exactly what it means to take the mathematical limit. It never actually solves what happens at infinity, it just takes you arbitrarily close to infinity. Another way to think of it is asking what happens on the threshold of infinity just before we actually reach it. This idea is extremely useful in a lot of mathematics where we need to resolve what happens as a sum of purchase a number but never actually reaches it. This idea of approaching something but never actually reaching it is the big idea at the heart of calculus.
Going back to the Zeno’s journey we can now see how the paradox is resolved. Not only does the infinite series sum to a finite answer, but that finite answer is the same one that common sense tells us is true. Zeno’s journey takes \(1\ hr.\)
See Also
References
Palmer, John (2021). “Zeno of Elea”. The Philosophers’ Magazine (92): 72–78. doi:10.5840/tpm20219216. ISSN 1354-814X.
Rossetti, Livio (1988). “The Rhetoric of Zeno’s Paradoxes”. Philosophy & Rhetoric. 21 (2): 145–152. ISSN 0031-8213.
Sherwood, John C. (2000). “Zeno of Elea”. In Roth, John K. (ed.). World Philosophers and Their Works. Salem Press. ISBN 978-0-89356-878-8.