There are only two kinds of certain knowledge: Awareness of our own existence and the truths of mathematics
Jean le Rond d’Alembert
Concept of Infinity
In the 1920s, the German mathematician David Hilbert) devised a famous thought experiment to show how hard it is to wrap our minds around the concept of infinity.

Story 1: No Vacancy at The Grand Hotel
Imagine a hotel with an infinite number of rooms and a very hardworking night manager. One night, the infinite Hotel is completely full, totally booked up with an infinite number of guests.
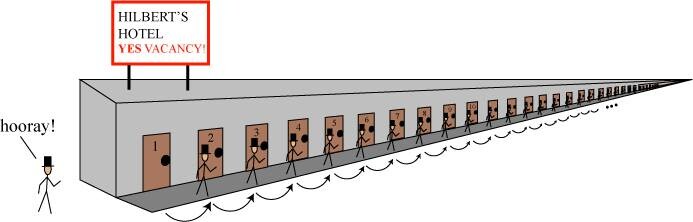
A man walks into the hotel and asks for a room. Rather than turn him down, the night manager decides to make room for him.
How?

He asks the guest in room number 1 to move to room number 2, the guest in room number 2 to move to room number 3, and so on. Every guest moves from room number n to room number n+1. Since there is an infinite number of rooms, there is a new room for each existing guest. One who leaves room open for the new customer. The process can be repeated for any finite number of new guests.
There may not be a last room , but there’s always a next room.
Let us Visualize:
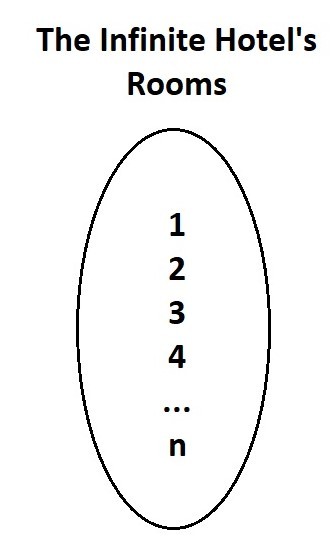
The rooms as a set ranging from 1 to an infinite number n. There isn’t the last room, but there is always the next room. So the trick is to simultaneously move each person to the next room.
Mapping
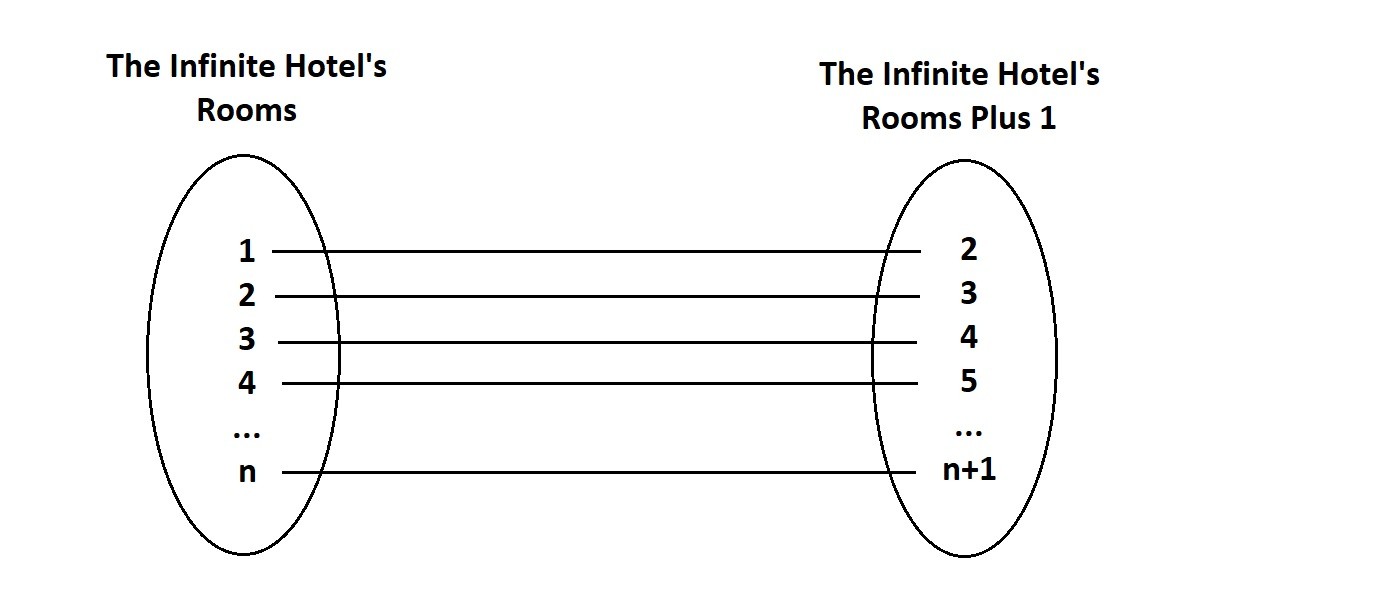
After we move all the guests we are left with room 1 unoccupied. In fact, we can use this same method to free up any finite number of rooms we need whether it’s 1, 50, or 50 million. Pretty nifty huh?
Story 2: An Infinite Bus Arrives
If, say, a tour bus unloads 40 new people looking for rooms, then every existing guest just moves from room number n to room number n+40, thus opening up the first 40 rooms, but now an infinitely large bus with a countably infinite number of passengers pulls up to rent rooms (countably infinite is the key). Now, the infinitely large bus of infinite passengers perplexes the night manager at first, but he realizes there’s a way to place each new person. He asks the guest in room number 1 to move to room number 2. He then asks the guest in room number 2 to room number 4 and room number 3 to room number 6 and so on.
Each current guest moves from room number ‘n’ to room number 2n filling up only the infinite even-numbered rooms. By doing this , he has now emptied all of the infinitely many odd-numbered rooms, which are then taken by the people filling off the infinite bus.
Let’s us Visualize
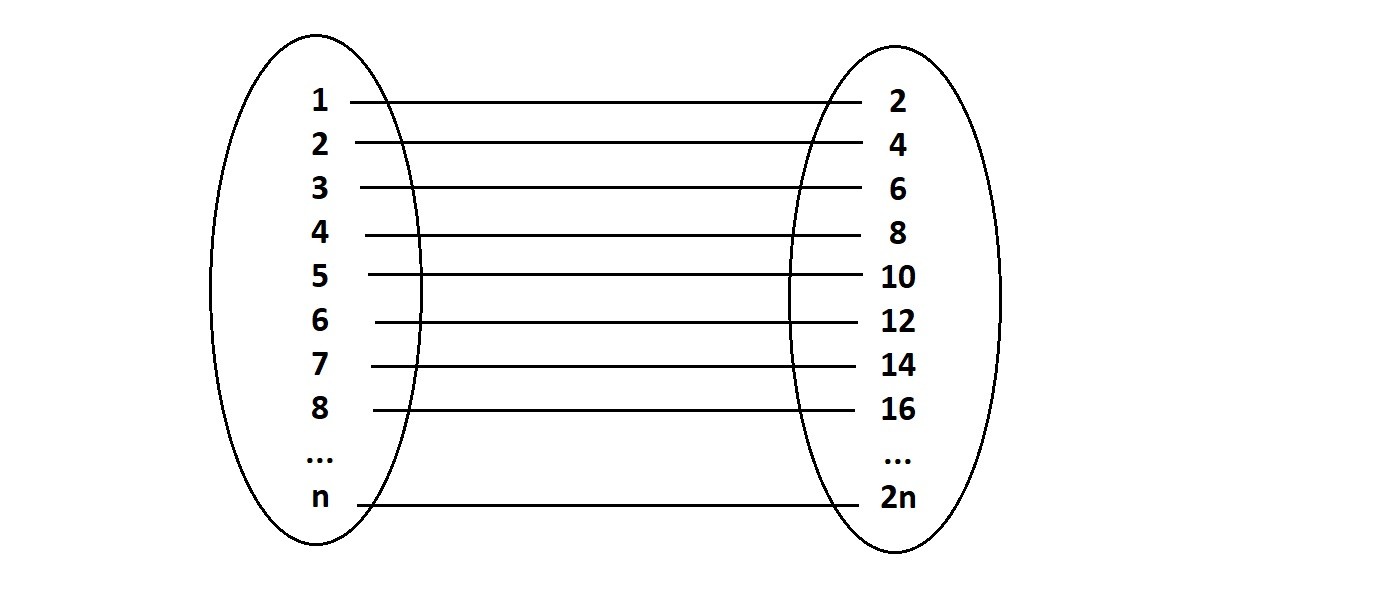
If we move each current guest to 2 times their current room number, we’ll find a new room for each of the current infinite guests and be able to put all of our new guests in the infinite set of odd-numbered rooms left over.
You just took an infinite set, split it into two equivalent infinite sets both of which are the same size as the original infinite set yet also the same as the original infinite set itself when combined
That’s perfectly paradoxical!
Everyone is happy and the hotel’s business is booming more than ever. Actually, it’s booming exactly the same amount as ever, banking an infinite number of rupees a night. Word spreads about this incredible hotel. People pour in from far and wide.
Story 3: An Infinite Number of Infinite Busses Arrives
One night, the unthinkable happens. The night manager looks outside and sees an infinite line of infinitely large buses, each with a countably infinite number of passengers.
What Can he do?

If he can’t find the rooms for them, the hotel will lose out on an infinite amount of money, and he will surely lose his job. Luckily, he remembers that around the year 300 B.C.E., Euclid proved that there is an infinite quantity of prime.) numbers.
So to accomplish this seemingly impossible task of finding infinite beds for infinite buses of infinite weary travelers, the night manager assigns every current guest to the first prime number 2 raised to the power of their current room number.
The current occupant of room number 7 goes to room number which is room 128. The night manager then takes the people on the first of the infinite buses and assigns them to the room number of the next prime, 3, raised to the power of their seat number on the bus. So, the person in seat number 7 on the first bus goes to room number or room number 2187.
This continues all of the first buses. The passenger on the second bus is assigned powers of the next prime, 5. The following bus, powers of 7. Each bus follows the power of 11, powers of 13, powers of 17, etc. Since each of these numbers only has 1 and the natural number powers of their prime number base as factors, there are no overlapping room numbers. All of the buses’ passengers fan out into rooms using unique room assignment schemes based on unique prime numbers. In this way, the night manager can accommodate every passenger on every bus. Although, there will be many rooms that go unfilled, like room 6, since 6 is not a power of any prime number. Luckily, his bosses weren’t very good at mathematics, so his job is safe.
The night manager’s strategies are only possible because while the infinite hotel is certainly a logistical nightmare, it only deals with the lowest level of infinity, mainly, the countable infinity of the natural numbers, 1,2,3,4 and so on.
Georg Cantor) called this level ‘infinity aleph-zero.)’ We use natural numbers for the room numbers as well as the seat numbers on the buses. If we are dealing with higher orders of infinity, such as that of the real numbers, these structured strategies would no longer be possible as we have no way to systematically include every number.
The real number infinite hotel has negative number rooms in the basement, fractional rooms, so the guy in room ½ always suspects he has less room than the guy in room 1. Square root rooms, like room radical 2, and room π, where the guests expect free desert.
What self-respecting night manager would ever want to work there even for an infinite salary?
At Hilbert’s infinite hotel, where there’s never any vacancy and always room for more, the scenarios faced by the ever-diligent and may be too hospitable night manager serves to remind us of just hard it is for our relatively finite minds to grasp a concept of as larger as infinity. Maybe you can help tackle these problems after a good night’s sleep. But honestly, we might need someone to change rooms at 2 am.