Set Theory Demystified
Functions, Mappings, and the Rich Tapestry of Finite and Infinite Sets
Preliminaries
0.0 Basic Set Operations
Modern analysis, like most other subfields of modern mathematics, is concerned with numbers, sets, and geometry. Here, set theory is not our focus. Almost every other branch of mathematics relies on the set theory as part of its foundation, so it’s important to get at least some grounding in set theory before doing other advanced areas of mathematics.
Definition: (Informal)
We define a set \(A\) to be any unordered collection of objects, e.g., \(\{3,8,5,2\}\) is a set. If \(x\) is an object, we say that \(x\) is an element of \(A\) or \(x \in A\) if \(x\) lies in the collection; otherwise we say that \(x \notin A.\) For instance, \(3 \in \{1,2,3,4,5\}\) but \(7 \notin \{1,2,3,4,5\}.\)
This definition is intuitive enough, but it doesn’t answer a number of questions, such as which collections of objects are considered to be sets, which sets are equal to other sets, and how one defines operations on sets (e.g., unions, intersections, etc.). Also, we have no axioms yet on what sets do, or what their elements do. Obtaining these axioms and defining these operations will be the purpose of the remainder of this section. We first clarify one point: we consider sets themselves to be a type of object.
Axiom 0.1
If \(A\) is a set, then \(A\) is also an object. In particular, given two sets \(A\) and \(B\), it is meaningful to ask whether \(A\) is also an element of \(B\).
Example: (informal) The set \(\{3, \{3, 4\}, 4\}\) is a set of three distinct elements, one of which happens to itself be a set of two elements.
Remark 1
There is a special case of set theory, called “pure set theory”, in which all objects are sets; for instance, the number \(0\) might be identified with the empty set \(\phi\) = \(\{\}\), the number \(1\) might be identified with \(\{0\}\) = \(\{\{\}\}\), the number \(2\) might be identified with \(\{0,1\} = \{\{\},\{\{\}\}\},\) and so forth. From a logical point of view, pure set theory is a simpler theory, since one only has to deal with sets and not with objects; however, from a conceptual point of view, it is often easier to deal with impure set theories in which some objects are not considered to be sets. The two types of theories are more or less equivalent for the purposes of doing mathematics, and so we shall take an agnostic position as to whether all objects are sets or not. For instance, we do not insist that a natural number such as \(3\) be identified with a set as indicated above. (The more accurate and mathematically useful statement is that natural numbers can be the cardinalities of sets, rather than necessarily being sets themselves.)
To summarize so far, among all the objects studied in mathematics, some of the objects happen to be set; and if \(x\) is an object and \(A\) is a set, then either \(x \in A\) is true or \(x\in A\) is false. ( If \(A\) is not a set, we leave the statement \(x \in A\) undefined; for instance, we consider the statement \(3 \in 4\) to neither be true nor false, but simply meaningless, since \(4\) is not a set.)
Next, we try to capture the notion of equality: when are two sets considered to be equal? We do not consider the order of the elements inside a set to be important; thus we think of \(\{3,8,5,2\}\) and \(\{2,3,5,8\}\) as the same set. On the other hand, \(\{3,8,5,2\}\) and \(\{3,8,5,2,1\}\) different sets, because the latter set contains an element that the former one does not, namely the element \(1\). For similar reasons \(\{3,8,5,2\}\) and \(\{3,8,5\}\) are different sets. We formalize this by a further axiom:
Axiom 0.2 (Equality of Sets)
Two sets A and B are equal, \(A = B\), iff every element of \(A\) is an element of \(B\) and vice versa. To put it another way, \(A = B\) if and only if every element \(x\) of \(A\) belongs also to \(B\), and every element \(y\) of \(B\) belongs also to \(A.\)
Thus, for instance, \(\{1,2,3,4,5\}\) and \(\{3, 4, 2, 1,5\}\) are the same set, since they contain exactly the same elements. (The set \(\{3,3, 1, 5, 2, 4, 2\}\) is also equal to \(\{1,2,3,4,5\}\); the repetition of \(3\) and \(2\) is irrelevant as it does not further change the status of \(2\) and \(3\) being elements of the set.)
The “is an element of” relation \(\in\) obeys the axiom of substitution. Because of this, any new operation we define on sets will also obey the axiom of substitution, as long as we can define that operation purely in terms of the relation \(\in\). This is for instance the case for the remaining definitions in this section. (On the other hand, we cannot use the notion of the “first” or “last” element in a set in a well-defined manner, because this would not respect the axiom of substitution; for instance, the sets \(\{1,2,3,4,5\}\) and \(\{3, 4, 2, 1,5\}\) are the same set, but have different first elements.)
Next, we turn to the issue of exactly which objects are sets and which objects are not. The situation is analogous to how we defined the natural numbers in the previous chapter; we started with a single natural number, \(0\), and started building more numbers out of \(0\) using the increment operation. We will try something similar here, starting with a single set, the empty set, and building more sets out of the empty set by various operations. We begin by postulating the existence of the empty set.
Axiom 0.3(Empty set)
There exists a set \(\phi,\) known as the empty set, which contains no elements, i.e., \(\forall x\ \text{we have}\ x \notin \phi.\)
The empty set is also denoted \(\{\}\). Note that there can only be one empty set; if there were two sets \(\phi\) and \({\phi}^{'}\) which were both empty, then by \(\text{Axiom 0.2}\) they would be equal to each other (why?).
If a set is not equal to the empty set, we call it non-empty. The following statement is very simple, but worth stating nevertheless:
Lemma (Single choice): Let \(A\) be a non-empty set. Then there exists an object \(x\) a such that \(x \in A\).
Proof: We prove by contradiction. Suppose there does not exist any object \(x\) such that \(x\in A\). Then for all objects \(x\) , we have \(x \notin A\). Also, by \(\text{Axiom 0.3}\) we have \(x \notin A\). Thus \(x \in A \iff x \notin \phi\) (both statements are equally false), and so \(A=\phi\) by \(\text{Axiom 0.2}\), a contradiction.
Remark 2
The above Lemma asserts that given any non-empty set \(A\), we are allowed to “choose” an element \(x\) of \(A\) which demonstrates this non-emptyness. Later on we will show that given any finite number of non-empty sets, say \(A_1….. A_n\) it is possible to choose one element \(x_1,\ldots\ldots x_n\)from each set \(A_1,…, A_n\); this is known as “finite choice”. However, in order to choose elements from an infinite number of sets, we need an additional axiom, the axiom of choice, which we will discuss later.
Note that the empty set is not necessarily the same thing as the natural number \(0\). One is a set; the other is a number. However, it is true that the cardinality of the empty set is \(0\).
If \(\text{Axiom 0.3}\) was the only axiom that set theory had, then set theory could be quite boring, as there might be just a single set in existence, the empty set. We now present further axioms to enrich the class of sets available.
Axiom 0.4(Singleton Sets and Pair sets)
If \(a\) is an object, then there exists a set \(\{a\}\) whose only element is \(a\), i.c., for every object \(y\), we have \(y \in \{a\}\)\(\iff y = a\); we refer to \(\{a\}\) as the singleton set whose element is \(a\). Furthermore, if \(a\) and \(b\) are objects, then there exists a set \(\{a, b\}\) whose only elements are \(a\) and \(b\); i.e., for every object \(y\), we have \(y \in \{a,b\}\)\(\iff y=a\ \text{or}\ y = b\); we refer to this set as the pair set formed by \(a\) and \(b\).
Remarks 3
Just as there is only one empty set there is only one singleton set for each object \(a\). Similarly, given any two objects \(a\) and \(b\), there is only one pair set formed by \(a\) and \(b\). Also, \(\text{Axiom 0.2}\) also ensures that \(\{a,b\}= \{b,a\}\) (why?) and \(\{a, a\}=\{a\}\) (why?). Thus the singleton set axiom is in fact redundant, being a consequence of the pair set axiom. Conversely, the pair set axiom will follow from the singleton set axiom and the pairwise union axiom below. One may wonder why we don’t go further and create triplet axioms, quadruplet axioms, etc.; however, there will be no need for this once we introduce the pairwise union axiom below.
Example
Since \(\phi\) is a set (and hence an object), the singleton set \(\{0\}\), i.e., the set whose only element is \(\{0\}\), is also a set. Similarly, the singleton set \(\{\{0\}\}\) and the pair set \(\{0, \{0\}\}\) are also sets. These four sets are not equal to each other.
As the above examples show, we can now create quite a few sets; however, the sets we make are still fairly small (each set that we can build consists of no more than two elements, so far). The next axiom allows us to build somewhat larger sets than before.
Axiom 0.5 (Pairwise Union)
Given any two sets \(A, B\), there exists a set \(A \cup B\), called the union of \(A\) and \(B\), which consists of all the elements that which belong to \(A\ or\ B\) or both. In other words, for any object, \(x\)
\[ x \in A\cup B \iff (x \in A \ or\ x \in B) \]
or refers by default in mathematics to inclusive or: “\(X\) or \(Y\) is true or both are true.”
Examples: The set \(\{1,2\} \cup \{2, 3\}\) consists of those elements which either lie on \(\{1, 2\} \ or\ in\ \{2,3\}\) or in both, or in other words the elements of this set are simply \(1, 2\), and \(3\). Because of this, we denote this set as \(\{1,2\} \cup \{2, 3\}= \{1,2,3\}.\)
Remark 4
If \(A, B, A'\) are sets, and \(A\) is equal to \(A'\), then \(A\cup B\) is equal to \(A'\cup B\) (why? One needs to use \(\text{Axiom 0.4 and Axiom 0.2}\)). Similarly if \(B'\) is a set which is equal to \(B\), then \(A \cup B\) is equal to \(A \cup B'\). Thus the operation of union obeys the axiom of substitution, and is thus well-defined on sets.
Now, we will introduce other axioms of set theory which allow one to construct arbitrarily large, and even infinite sets.
Clearly, some sets seem to be larger than others. One way to formalize this concept is through the notion of a subset.
Subsets
Let \(A\) and \(B\) be sets We say that \(A\) is a subset of \(B\), denoted \(A \subseteq B\), iff every element of \(A\) is also an element of \(B\). i.e.
\[ \forall \ x, x \in A \implies x \in B. \]
We say that \(A\) is a proper subset of \(B,\) denoted \(A \subset B,\) if \(A \subseteq B\) and \(A \not= B.\)
Remarks 5
Because these definitions involve only the notions of equality and the “is an element of” relation, both of which already obey the axiom of substitution, the notion of subset also automatically obeys the axiom of substitution. Thus for instance if \(A \subseteq B\) and \(A = A'\), then \(A' \subseteq B\).
Examples: We have \(\{1,2,4\} \subseteq \{1,2,3,4,5\}\), because every element of \(\{1, 2, 4\}\) is also an element of \(\{1, 2, 3, 4, 5\}\). In fact we also have \(\{1,2,4\} \subset \{1,2,3,4,5\}\), since the two sets \(\{1,2,4)\) and \(\{(1,2,3,4,5\}\) are not equal. Given any set \(A\), we always have \(A\subseteq A\) (why?) and \(\phi \subseteq A\) (why?).
The notion of subset in set theory is similar to the notion of “less than or equal to” for numbers, as the following proposition demonstrates
Proposition(Sets are partially ordered by set inclusion)
Let \(A, B, C\) be sets. If \(A\subseteq B\) and \(B\subseteq C\) then \(A \subseteq C\). If \(A \subseteq B\) and \(B \subseteq A\), then \(A=B\). Finally, if \(A\subset B\) and \(B \subset C\) then \(A \subset C\).
Proof: We shall just prove the first claim. Suppose that \(A \subseteq B\) and \(B \subseteq C\) . To prove that \(A \subseteq C\), we have to prove that every element of \(A\) is an element of \(C\). So, let us pick an arbitrary element \(x\) of A. Then, since \(A \subseteq B\), \(x\) must then be an element of \(B\). But then since \(B \subseteq C\), \(x\) is an element of \(C\). Thus every element of \(A\) is indeed an element of \(C\), as claimed.
The subset relation and the union operation are related to each other. We now give an axiom which easily allows us to create subsets out of larger set.
Axiom 0.6(Axiom of Specification)
Let \(A\) be a set, and for each \(x \in A\), let \(P(x)\) be a property pertaining to \(x\) (i.e., for each \(x \in A\), \(P(x)\) is either a true statement or a false statement). Then there exists a set, called \(\{x \in A: P(x)\ is\ true\}\) (or simply \(\{x \in A: P(x)\} for\ short)\), whose elements are precisely the elements \(x \in A\) for which \(P(x)\) is true. In other words, for any object \(y\),
\[ y \in \{x \in A: P(x)\ is\ true \} \iff (y \in A \ and \ P(y) \ is\ true). \]
This axiom is also known as the axiom of separation. Note that \(\{x \in A: P(x)\ is\ true\}\) is always a subset of \(A\), though it could be as large as \(A\) or as small as the empty set. One can verify that the axiom of substitution works for specification, thus if \(A = A'\) then \(\{x \in A: P(x)\} = \{x \in A': P(x)\}\)
Example: Let \(S=\{1,2,3,4,5\}\). Then the set \(\{n\in S:n <4\}\) is the set of those elements \(n\) in \(S\) for which \(n < 4\) is true, i.e., \(\{(n \in S: n<4\} = \{1,2,3\}\) Similarly, the set \(\{(n \in S: n<7\}\) is the same as \(S\) itself, while \(\{(n \in S: n<1\}\) is the empty set.
We sometimes \(\{x \in A | \ P(x)\}\) write instead of \(\{x \in A : \ P(x)\}\) this is useful when we are using the colon “:” to denote something else, for instance, to denote the domain and codomain of a function \(f: X \rightarrow Y\). We also describe \(\{x \in A : \ P(x)\}\) in words as “the set of all in \(A\) such that \(P(x)\) is true”.
We can use this axiom of specification to define some further operations on sets, namely intersections and difference sets.
Definitions
The intersection \(S_1 \cap S_2\) of two sets is defined to be the set,
\[S_1 \cap S_2:= \{x \in S_1: x \in S_2\}\]
In other words, \(S_1 \cap S_2\) consists of all the elements which belong to both \(S_1\) and \(S_2\). Thus, for all objects \(x,\)
\[x \in S_1 \cap S_2 \iff x \in S_1 \ and\ x\in S_2\]
Note that this definition is well-defined. Because it is defined in terms of more primitive operations which were already known to obey the axiom of substitution.
Examples:
We have \(\{1,2,4\} \cap \{2, 3, 4\}=\{2,4\}, \{1,2\} \cap \{3,4\} =\phi, \{2,3\} \cup \phi = \{2,3\}, \ and\ \{2,3\} \cap \phi = \phi\).
By the way, one should be careful with the English word “and”: rather confusingly, it can mean either union or intersection, depending on context. For instance, if one talks about a set of “boys and girls”, one means the union of a set of boys with a set of girls, but if one talks about the set of people who are single and male, then one means the intersection of the set of single people with the set of male people. (Can you work out the rule of grammar that determines when “and” means union and when “and” means intersection?) Another problem is that “and” is also used in English to denote addition, thus for instance one could say that ” \(2\) and \(3\) is \(5\) “, while also saying that”the elements of \(\{2\}\) and the elements of \(\{3\}\) form the set \(\{2,3\}\) ” and “the elements in \(\{2\}\) and \(\{3\}\) form the set \(\phi\)”. This can certainly get confusing! One reason we resort to mathematical symbols instead of English words such as “and” is that mathematical symbols always have a precise and unambiguous meaning, whereas one must often look very carefully at the context in order to work out what an English word means.
Two sets \(A, B\) are said to be disjoint if \(A \cap B=\phi.\) Note that this is not the same concept as being distinct, \(A \not= B\). For instance, the sets \(\{1,2,3\} \ and\ \{2,3,4\}\) are distinct (there are elements of one set which are not elements of the other) but not disjoint (because their intersection is non-empty). Meanwhile, the sets \(\phi\) and \(\phi\) are disjoint but not distinct (why?). There is an operation on sets that is somewhat analogous to subtraction:
Definition (Difference sets)
Given two sets \(A\) and \(B\), we define the set \(A-B\) or \(A \setminus B\) to be the set \(A\) with any elements of \(B\) removed:
\[ A \setminus B := \{ x \in A: x \notin B \}; \]
For instance, \(\{1,2,3,4\} \setminus \{2,4,6\} = \{1,3\}.\) In many cases \(B\) will be a subset of \(A\), but not necessarily.
We now give some basic properties of unions, intersections, and difference sets.
Proposition (Sets Form a Boolean Algebra)
Let \(A, B, C\) be sets, and let \(X\) be a set containing \(A, B, C\) as subsets.
(a) (Minimal element) We have \(A\cup \phi= A\) and \(A\cap \phi = \phi\).
(b) (Maximal element) We have \(A \cup X = X\) and \(A\cap X = A.\)
(c) (Identity) We have \(A\cap A =A\) and \(A\cup A = A\).
(d) (Commutativity) We have \(A\cup B = B\cup A\) and \(A\cap B = B\cap A.\)
(e) (Associativity) We have \((A\cup B) \cup C= A\cup (B\cup C)\) and \((A\cap B)\cap C= A\cap (B\cap C).\)
(f) (Distributivity) We have \(A\cap (B\cup C) = (A\cap B) \cup (A\cap C) \ and \ A\cup (B\cap C)= (A\cup B)\cap (A\cup C).\).
(g) (Partition) We have \(A\cup (X\setminus A) = X \ and\ A\cap (X\setminus A) = \phi\).
(h) (De Morgan laws) We have, \(X\setminus (A\cup B) = (X\setminus A) \cap(X\setminus B) \ and \ X\setminus (A\cap B) = (X\setminus A) \cup(X\setminus B).\)
Remark
The reader may observe a certain symmetry in the above laws between \(\cup\) and \(\cap\), and between \(X\) and \(\phi\). This is an example of duality - two distinct properties or objects being dual to each other. In this case, the duality is manifested by the complementation relation \(A\mapsto X\setminus A;\) the de Morgan laws assert that this relation converts unions into intersections and vice versa. (It also interchanges \(X\) and the empty set.) The above laws are collectively known as the laws of Boolean algebra, after the mathematician George Boole (1815-1864), and are also applicable to a number of other objects other than sets; they play a particularly important role in mathematical logic.
We have now accumulated a number of axioms and results about sets, but there are still many things we are not able to do yet. One of the basic things we wish to do with a set is take each of the objects of that set, and somehow transform each such object into a new object; for instance we may wish to start with a set of numbers, say \(\{3,5,9\}\), and increment each one, creating a new set \(\{4, 6, 10\}\). This is not something we can do directly using only the axioms we already have, so we need a new axiom:
Axiom 0.7(Replacement)
Let \(A\) be a set. For any object \(x \in A\), and any object \(y\), suppose we have a statement \(P(x, y)\) pertaining to \(x\) and \(y\), such that for each \(x \in A\) there is at most one \(y\) for which \(P(x, y)\) is true. Then there exists a set \(\{y: P(x,y)\ is \ true \ for \ some\ x \in A\}\), such that for any object \(z\),
\[ z \in \{y: P(x,y)\ is \ true \ for \ some\ x \in A\} \iff\ P(x,y)\ is \ true \ for \ some\ x \in A. \]
Let \(A= \{3,5,9\}\), and let \(P(x, y)\) be the statement \(y= x++\), i.e., \(y\) is the successor of \(x\). Observe that for every \(x \in A\), there is exactly one \(y\) for which \(P(x, y) is \ true\) - specifically, the successor of \(x\). Thus the above axiom asserts that the set \(\{y: y=x++ \ for \ some\ x \in \{3,5,9\}\}\) exists; in this case, it is clearly the same set as \(\{4,6, 10\}\).
Example: Let \(A = \{3,5,9\}\), and let \(P(x,y)\) be the statement \(y= 1\). Then again for every \(x\in A\), there is exactly one \(y\) for which \(P(x,y)\) is true specifically, the number \(1\). In this case \((y: y=1 \ for\ some\ x \in \{3,5,9\}\}\) is just the singleton set \(\{1\}\); we have replaced each element \(3,5,9\) of the original set \(A\) by the same object, namely \(1\). Thus this rather silly example shows that the set obtained by the above axiom can be “smaller” than the original set.
We often abbreviate a set of the form
\[ \{ y: y= f(x) \ for\ some \ x \in A\} \]
as \(\{f(x): x\in A\}\) or, \(\{f(x)| x\in A\}.\) Thus for instance, if \(A= \{3,5,9\},\ then\ \{x++: x\in A\}\) is the set (4,6, 10). We can of course combine the axiom of replacement with the axiom of specification, thus for instance we can create sets such as \(\{f(x) : x\in A ; P(x) \ is \ true\}\) by starting with the set \(A\), using the axiom of specification to create the set \(\{x \in A: P(x)\ is\ true\}\), and then applying the axiom of replacement to create \(\{f(x) : x\in A ; P(x) \ is \ true\}\). Thus for instance \(\{n++: n \in \{3,5,9\}; n<6 \} = \{4,6\}\)
In many of our examples we have implicitly assumed that natural numbers are in fact objects. Let us formalize this as follows.
Axiom 0.8(Infinity)
There exists a set \(\mathbb{N}\), whose elements are called natural numbers, as well as an object \(0\) in \(\mathbb{N}\) and an object \(n++\) assigned to every natural number \(n\in \mathbb{N}\), such that the Peano axioms (Axioms 1.1 and 1.5 holds)
There’s an assumption which says that \(\exists\ \text{a number sytem } \mathbb{N}\) \(\text{ whose elements}\) \(\text{we will call natural numbers, for which}\) Axioms 1.1 and 1.5 holds true.
This is the more formal version of the above assumptions. It is called the axiom of infinity because it introduces the most basic example of an infinite set, namely the set of natural numbers \(\mathbb{N}\). From the axiom of infinity we see that numbers such as \(3, 5, 7,\) etc. are indeed objects in set theory, and so (from the pair set axiom and pairwise union axiom) we can indeed legitimately construct sets such as \(\{3,5,9\}\) as we have been doing in our examples.
One has to keep the concept of a set distinct from the elements of that set; for instance, the set \(\{n+3: n \in \mathbb{N}, 0 \le n \le 5\}\) is not the same thing as the expression or function \(n +3\). We emphasize this with an example:
Example: This example requires the notion of subtraction, which has not yet been formally introduced. The following two sets are equal,
\[ \{n+3:n \in \mathbb{N}, 0 \le n \le 5\} = \{8-n: n \in \mathbb{N}, 0 \le n \le 5\} \hspace{1.5 cm}\ldots (*) \]
even though the expressions \(n + 3\) and \(8-n\) are never equal to each other for any natural number \(n\). Thus, it is a good idea to remember to use those curly braces \(\{\}\) when you talk about sets, lest you accidentally confuse a set with its elements. One reason for this counter-intuitive situation is that the letter n is being used in two different ways on the two sides of \((*)\). To clarify the situation, let us rewrite the set \(\{8-n: n \in \mathbb{N}, 0 \le n \le 5\}\) by replacing letter \(n\) by the letter \(m\), thus giving \(\{8-m: m \in \mathbb{N}, 0 \le m \le 5\}.\) This is exactly the same set as before, so we can rewrite \((*)\) as
\[ \{n+3:n \in \mathbb{N}, 0 \le n \le 5\} = \{8-m: m \in \mathbb{N}, 0 \le m \le 5\}, \]
Now it is easy to see \(\text{(using Axiom 0.2)}\) why this identity is true: every number of the form \(n+3\), where \(n\) is a natural number between \(0 \ and \ 5\), is also of the form \(8-m\) where \(m:= 5-n\) (note that \(m\) is therefore also a natural number between \(0 \ and \ 5\)); conversely, every number of the form \(8-m\), where \(m\) is a natural number between \(0 \ and \ 5\), is also of the form \(n+3\), where \(n:= 5-m\) (note that \(n\) is therefore a natural number between \(0 \ and \ 5\)). Observe how much more confusing the above explanation of \((*)\) would have been if we had not changed one of the \(n's\) to an \(m\) first!
Formally, we can refer to \(\mathbb{N}\) as “the set of natural numbers”, but we shall often abbreviate this to simply “the natural numbers”. Similarly for some other sets that we will introduce later in this text; for instance \(\mathbb{Z}\) will be “the set of integers” but also the “integers”, \(\mathbb{R}\) will be the “set of real numbers” but also “the real numbers” or even just “the reals”, and so forth.
0.1 Relations
If \(A\) and \(B\) are the (not necessarily distinct) sets, we define their Cartesian Product to be
\[ A \times B = \{ (x,y)| \ x \in A, y \in B\} \]
Thus \(A \times B\) is the set of all ordered pairs with the first components coming from \(A\) and the second component from \(B.\) For example,
\[\{1,2\} \times \{ 2,3,4\} = \{(1,2),(1,3),(1,4),(2,2),(2,3),(2,4)\}\] \(\mathbb{R} \times \mathbb{R}\; \text{is the set of all ordered pairs of the real numbers}\) and usually denoted by \(\mathbb{R^2}.\) Since, each point in the plane can be represented uniquely by an ordered pair of real numbers ( once the axes are fixed ) and each ordered pair corresponds to a unique point, the plane is usually denonted by \(\mathbb{R^2}.\) Similarly, \(\mathbb{R^3} = \mathbb{R} \times \mathbb{R} \times \mathbb{R}\) denotes the 3-dimensional Euclidean space.
A binary relation on a set \(X\) is a subset \(R\) of \(X \times X.\) If \((x,y) \in \text{R}\) we say that \(x\) stands in the relation \(R\) to \(y.\) We will then write \(xRy\) for convenience. A relation is usually specified by a statement about \(x\) and \(y.\) For example, \(x\le y\) is a relation on \(\mathbb{R,}\) viz., \(\{(x,y)| x\in \mathbb{R}, y \in \mathbb{R}, x\le y \}.\) \(x\) and \(y\) have the same age is a relation on the set of all people.
Note:
A relation \(R\) on \(X\) is said to be reflexive if \(xRx \;\forall x \in X.\)
\(R\) is said to be symmetric if \(yRx\) holds whenever \(xRy\) holds.
\(R\) is said to be transitive if \(xRy , yRz \implies xRz\)
We often draw diagram to indicate the cartesian product of two sets \(A\) and \(B.\) However, it should be realized that this diagram may be a simplification. For example, if \(A:=\{ x\in \mathbb{R}|\ 1 \le x\le2\}\) and \(B:= \{y\in \mathbb{R}|\; 0 \le y \le 1\; \text{or}\;2\le y\le 3\},\) then instead of a rectangle, we should have a drawing such as fig.
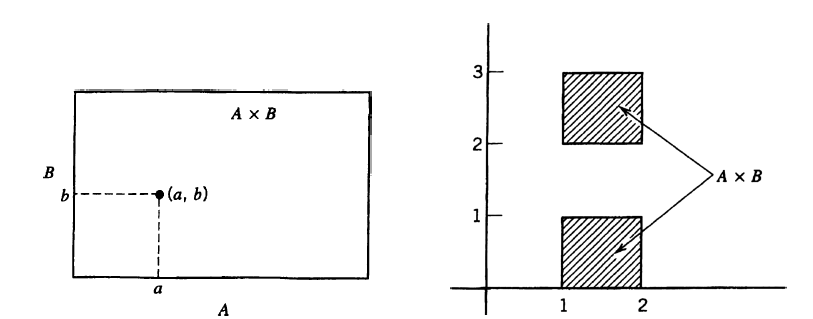
We will now discuss the fundamental notion of a function or a mapping.
Functions and Mappings
To the mathematician of the early \(19^{\text{th}}\) century, the word “function” meant a definite formula, such as \(f(x) = x^2+3x-5\) which associates to each real number \(x\) another number \(f(x).\) (Here, \(f(0)=-5, f(1)= -1,f(5)= 35.\)) This understanding excluded the case of different formulas on different intervals, so that could not be defined “in pieces.” As mathematics developed, it became clearer that a more general definition of function would be useful.
A function \(f\) from a set \(A\) into a set \(B\) is a rule of correspondence that assigns to each element \(x\) in \(A\) a uniquely determined element \(f(x)\) in \(B.\)
But, However suggestive this revised definition be, there is a difficulty of interpreting the phrase “rule of correspondence”. In order to clarify this, we will express the definition entirely in terms of sets; in effect, we will define a function to be its graph.
Definition
Let \(A\) and \(B\) be set. Then a function from \(A\) to \(B\) is a set \(f\) of ordered pairs in \(A \times B\) such that for each \(a \in A\) there exists a unique \(b\in B\) with \((a,b) \in f.\) (In other words, if \((a,b) \in f \;\text{and}\; (a,b^{'}) \in f\; \text{then}\; b=b^{'}.\) )
The set \(A\) of first elements of a function \(f\) is called the domain of \(f\) and is often denoted by \(D(f).\) The set of all second elements in \(f\) is called the range of \(f\) and is often denoted by \(R(f).\) Note that, although \(D(f) = A,\) we only have \(R(f) \subseteq B.\)
The essential condition that:
\[(a,b) \in f \; \text{and}\; (a,b^{'}) \in f \implies b=b^{'}\]
is sometimes called the vertical line test. In geometrical terms, it says every vertical line \(x=a\) with \(a \in A\) intersects the graph of \(f\) exactly once.
The notation
\[ f: A \rightarrow B \]
is often used to indicate that \(f\) is a function from \(A\) into \(B.\) We will also say that \(f\) is a mapping of \(A\) into \(B,\) or that \(f\) maps \(A\) into \(B.\) If \((a,b)\) is an element in \(f,\) it is customary to write
\[b = f(a)\; \text{or sometimes}\; a \mapsto b\] If \(b= f(a),\) we often refer to \(b\) as the value of \(f\) at \(a,\) or as the image of a under \(f.\)
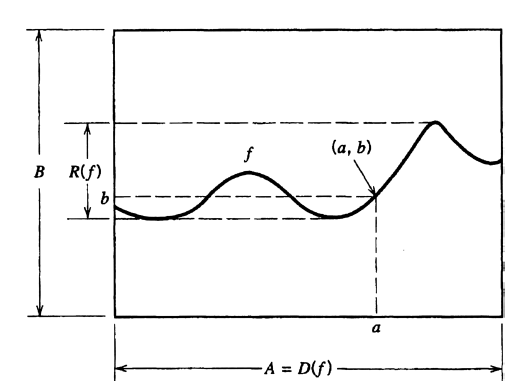
Mapping and Its Visual Meaning
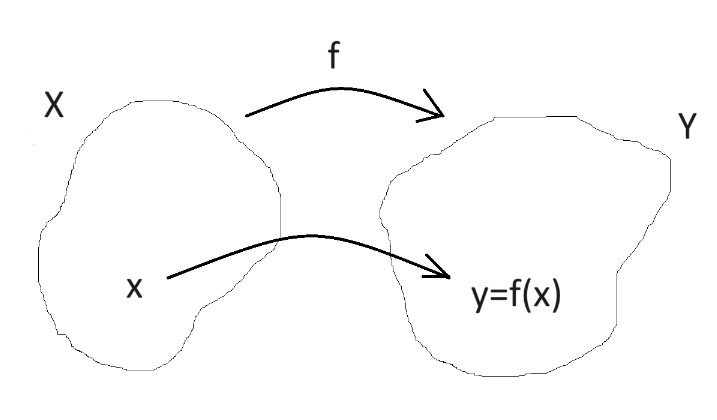
The notion of mapping (or function) is one of the most fundamental concepts in mathematics today. The intuitive concept of mapping is the following:
Let \(X\) and \(Y\) two non empty sets. By given some rule, if each element \(x \in X\) corresponds to a unique element \(y \in Y\) then that rule is called a map of \(X\) into \(Y\) and is denoted by \(f.\)
The words map or mapping, transformation; correspondence and operator are among some of the many that are sometimes used as synonyms for function.
The symbol
\[f: X \mapsto Y\] is sometimes used as an abbreviation for
“\(f\) is a function from \(X\) to \(Y\) “,
Or,
“\(f\) maps the set \(X\) into the set \(Y\) “
If \(x \in X\), then the element of \(Y\) which corresponds to \(x\) is denoted by \(f(x)\) and \(f(x)\) is called the image of \(x\) in \(Y\) under the map \(f\).
In the map \(f: X \mapsto Y\), \(X\) is called the domain of the map and the subset of the elements of \(Y\) which are images of some element of \(X\) is called the range of the map.
The figure given below gives a convenient way of picturing the function \(f: X \mapsto Y\).
On the left \(X\) and \(Y\) are different sets and on the right, they are equal\(-\) in which case we usually refer to \(f\) as a mapping of \(X\) into itself.
The mapping or funcction \(f\) is said to be well defined if
- every element \(x \in X\) has an image \(f(x)\) in \(Y,\)
- an element \(x \in X\) has only one image \(f(x)\) in \(Y\);
i.e., two or more elements of \(Y\) cannot be the image of the same element of \(X\). But it is possible that two or more elements of \(X\) may have the same image in \(Y\).
There may be also some elements in \(Y\) which may not be the image of any element in \(X\). 1) The following diagrams will make mapping more clear:
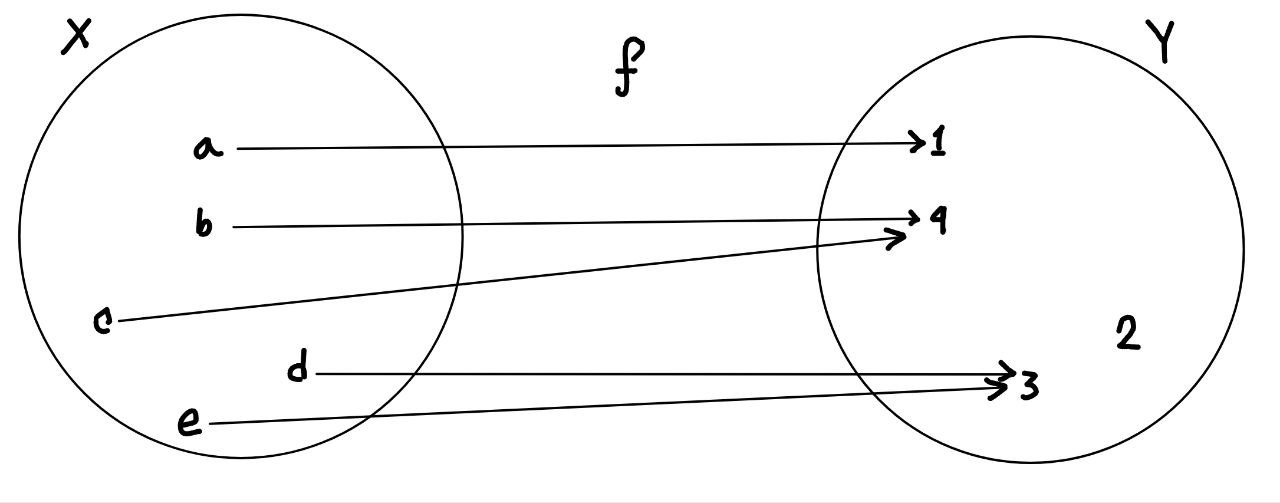
Note: A map \(f\) from \(X\) to \(Y\) is defined as a subset of \(X \times Y\) in which an ordered pair \((x,y) \in X \times Y\) occurs only one time with \(x\) as the first element.
2) This correspondence describes a mappings, because it satisfies our intuitive concept required of a correspondence to be called a mapping.
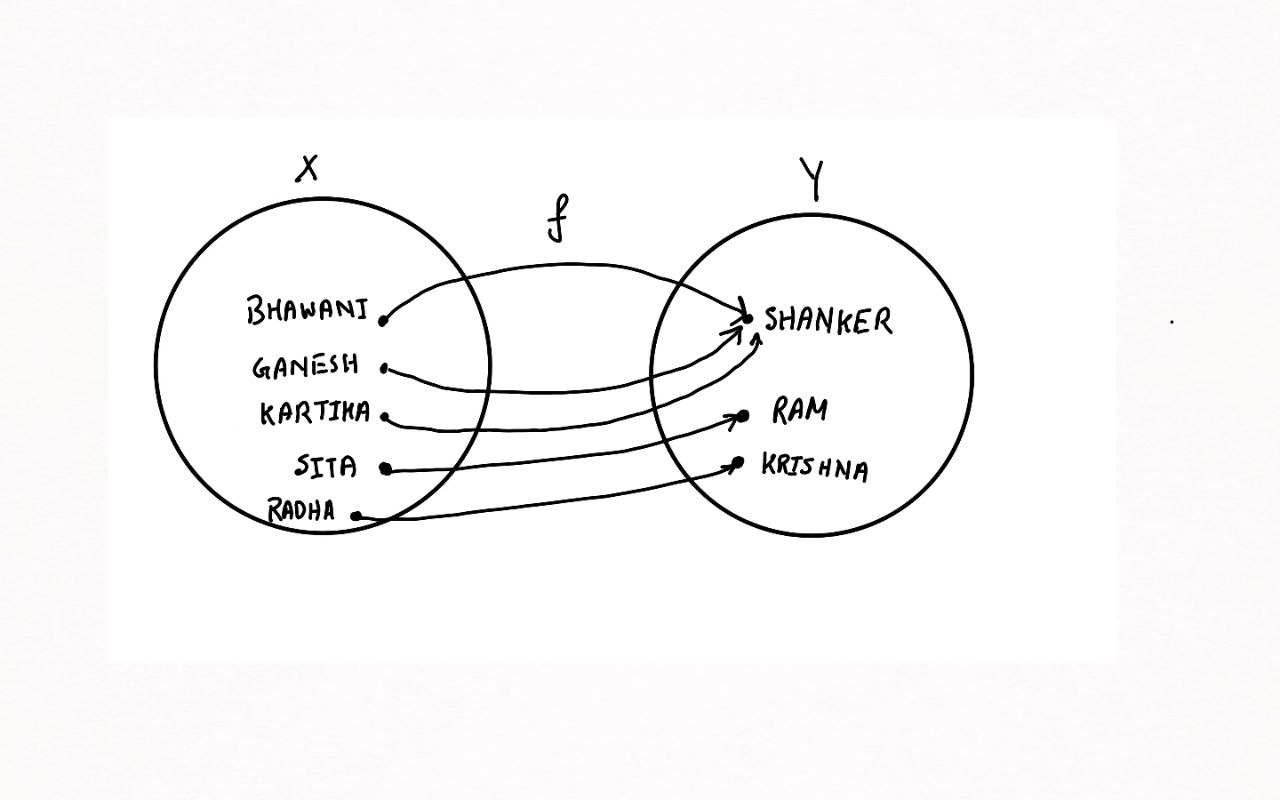
3) The following correspondance does not describe a mapping of the set \(X\) into set \(Y.\)
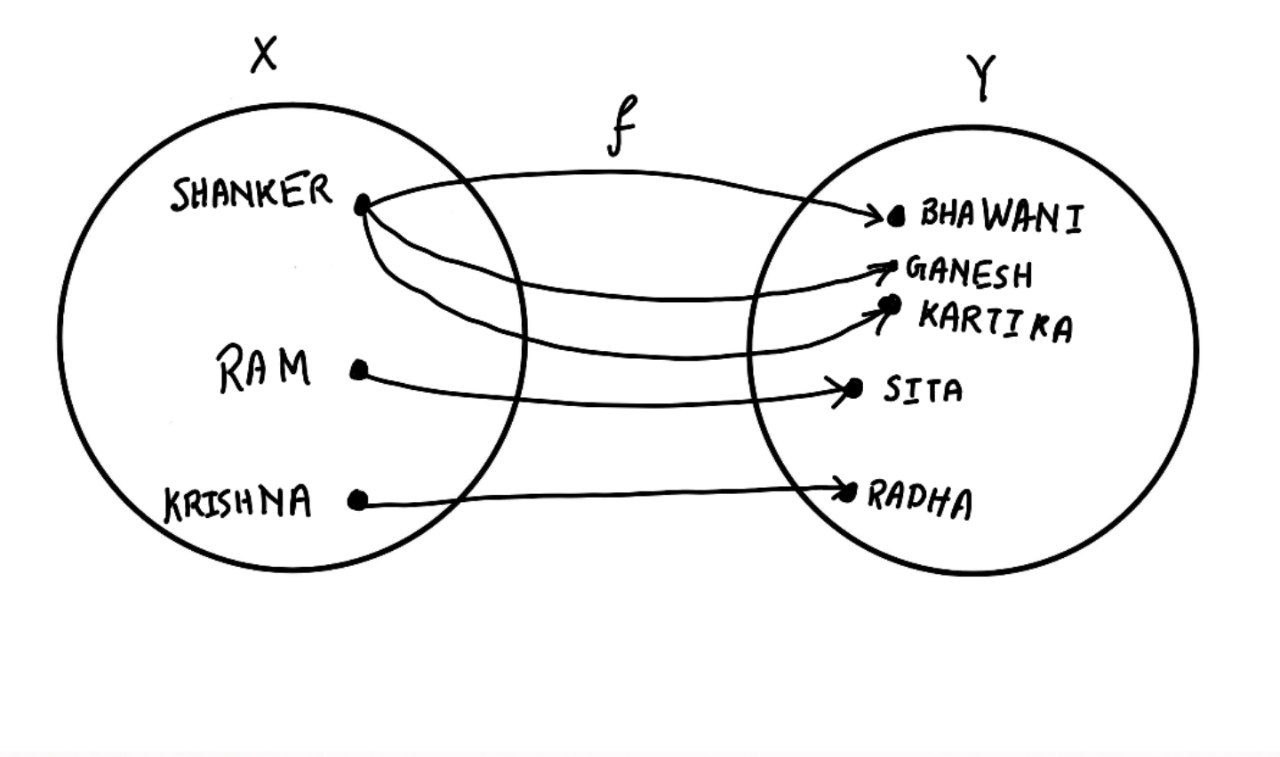
This is so because an element Shanker in \(X\) is associated with three different elements Bhawani, Ganesh, and Kartika in \(Y\).
Transformation and Machines
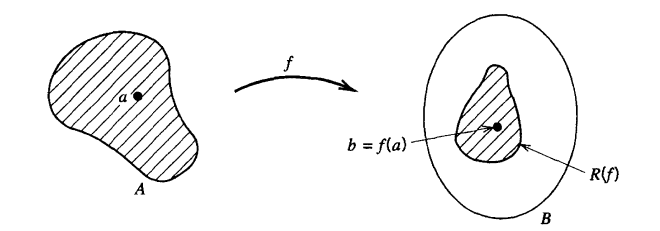
Aside from using graphs, we can visualize a function as a transformation of the set \(D(f)=A\) into the set \(R(f) \subseteq B.\) In this context, when \((a,b) \in f\) , We often draw a diagram, given below, even when sets \(A\)and \(B\) are not subsets of the plane.
There is another way of visualizing a function: namely, as a machine that accepts elements \(D(f) =A\) as inputs and produces corresponding elements of \(R(f) \subseteq B\) as outputs. If we take an element \(x \in D( f )\) and put it into \(f\), then out comes the corresponding value \(f (x)\). If we put a different element \(y \in D( f )\) into \(f\), then out comes \(f (y)\), which may or may not differ from \(f (x)\). If we try to insert something that does not belong to \(D( f )\) into \(f\),we find that it is not accepted, for \(f\) can operate only on elements from \(D( f )\).
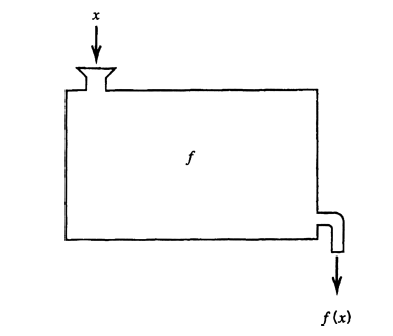
The last visualization makes the clear the distinction between \(f\) and \(f(x):\) the first is the machine itself, and the second is the output of the machine \(f\) when \(x\) is the input. Whereas no one is likely to confuse a meat grinder with ground meat, enough people have confused functions with their values that it is worth distinguishing between them notationally.