A Comprehensive Guide to Abstract Algebra
Unrevelling The Mystery
Motivation of Studying Abstract Algebra
Nurturing The Past
What is abstract algebra? based on the name alone, you might think it’s a similar algebra course most people take in high school, just a little more abstract. But if you open a book on abstract algebra, you’ll be in for quite a shock. It looks nothing like the algebra most people know about. So, to help you understand the subject, let’s go back in time. The year was 1800, and for some time now, people have known how to solve linear equations, quadratic equations, cubic equations, and even quartic equations. But what about equations of higher degree? Degree five, six, seven, and beyond?
Discovery of Group
A young teenager named Évariste Galois answered this question. And to do so, he used a tool that he called a “group”. Around this time, Carl Friedrich Gauss was busy making discoveries of his own. He ironed out a new technique called modular arithmetic which helped him solve many problems in number theory. Modular arithmetic shared many similarities to the groups used by Galois. The 1800s also saw a revolution in geometry. For more than 2,000 years, Euclid dominated the scene with his book The Elements, but mathematicians began to realize there are other geometries beyond the one devised by the ancient Greeks. It didn’t take long before groups were found to be a useful tool in studying these new geometries. It soon became clear that groups were a powerful tool that could be used in many different ways. So, it made sense to “abstract” out the common features of this tool used by Galois, Gauss, and others into a general tool, and then learn everything about it. Thus Group Theory was born.
And if “groups” were so useful, it’s natural to ask: would this approach work elsewhere?
Evolution of Abstract Algebra
Soon, new abstract objects began to take shape: rings, fields, vector spaces, and modules this didn’t happen overnight. It took years of hard work to find the right definitions. Too specific, and they wouldn’t be very useful. Too general, and they would be kind of boring and not very useful. But eventually, the right definitions were identified. Altogether, they form the subject we now call Abstract Algebra. At first glance, abstract algebra may not seem very applicable to the world around us. But it’s a young subject, and its usefulness continues to grow. Every year, new uses of abstract algebra are found, and not just in mathematics. Physics, chemistry, computer science, and other areas are discovering just how useful abstract algebra can be.
Quick note - ‘abstract algebra’ is sometimes called ‘modern algebra’. And if you are ever at a cocktail party with mathematicians, they will simply call it “algebra”.
So, when are you ready to begin learning abstract algebra? First, you really need to know the more familiar algebra, but the most important requirements are mathematical experience and mental maturity. Have you seen many mathematical proofs before? Are you able to think very abstractly? If so, then get ready, abstract algebra will challenge you like never before.
Group
Motivation of Group
There are many different areas of mathematics: geometry, number theory, topology, and algebra and the problems in these fields can be very different from one another. But in the late 1800s, people noticed they were using the same tool to solve many different kinds of problems. This sparked an idea: instead of reinventing the wheel, why not lift the tool out of the different branches of math and study the full power of the tool in a general form? This led to the creation of a new subject called abstract algebra, and the star of this field is a structure called the ‘Group’.
Group From Different Point of View
Before we give the definitions of a group, let’s see few examples. This will highlight the wide variety of groups and help we appreciate why it took a while for mathematicians to recognize that they were using the same tool in completely different settings.
Clock Arithmetic or Modular Arithmetic
To begin, imagine you live on an alien planet where each day in

If the hour hand starts at
Symmetries of a triangle
For our next example let’s look at an equilateral triangle. We’ll number the three corners
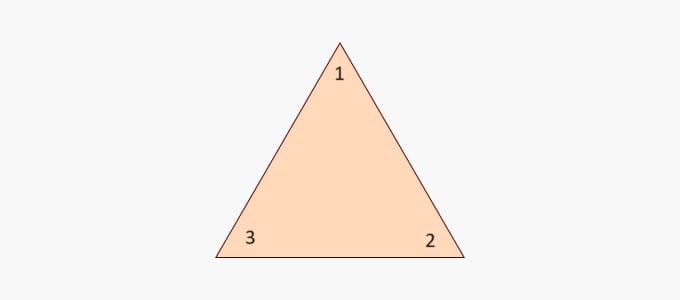
Here is the puzzle: How many different ways can you rotate & flip the triangle so it looks the same before and after?
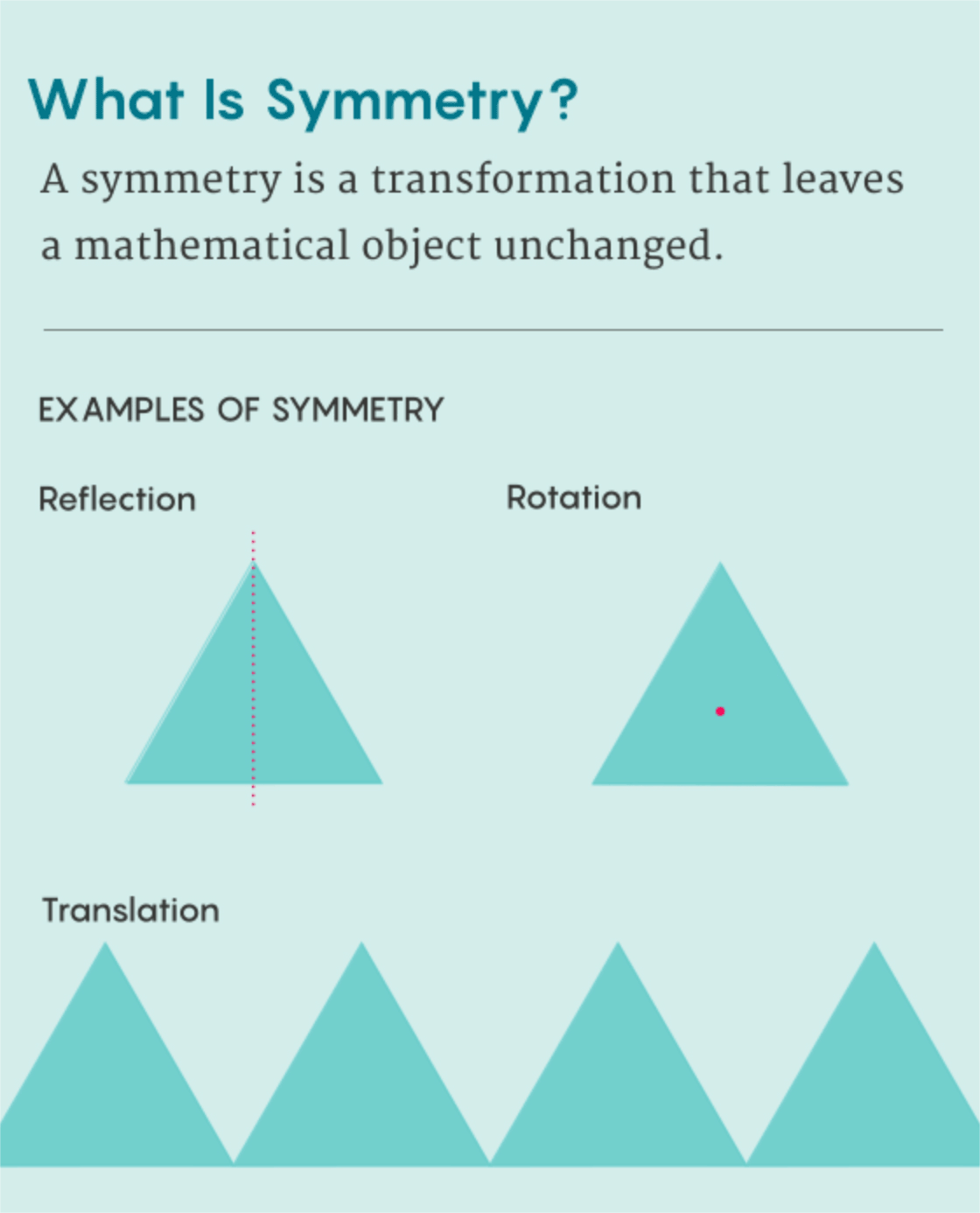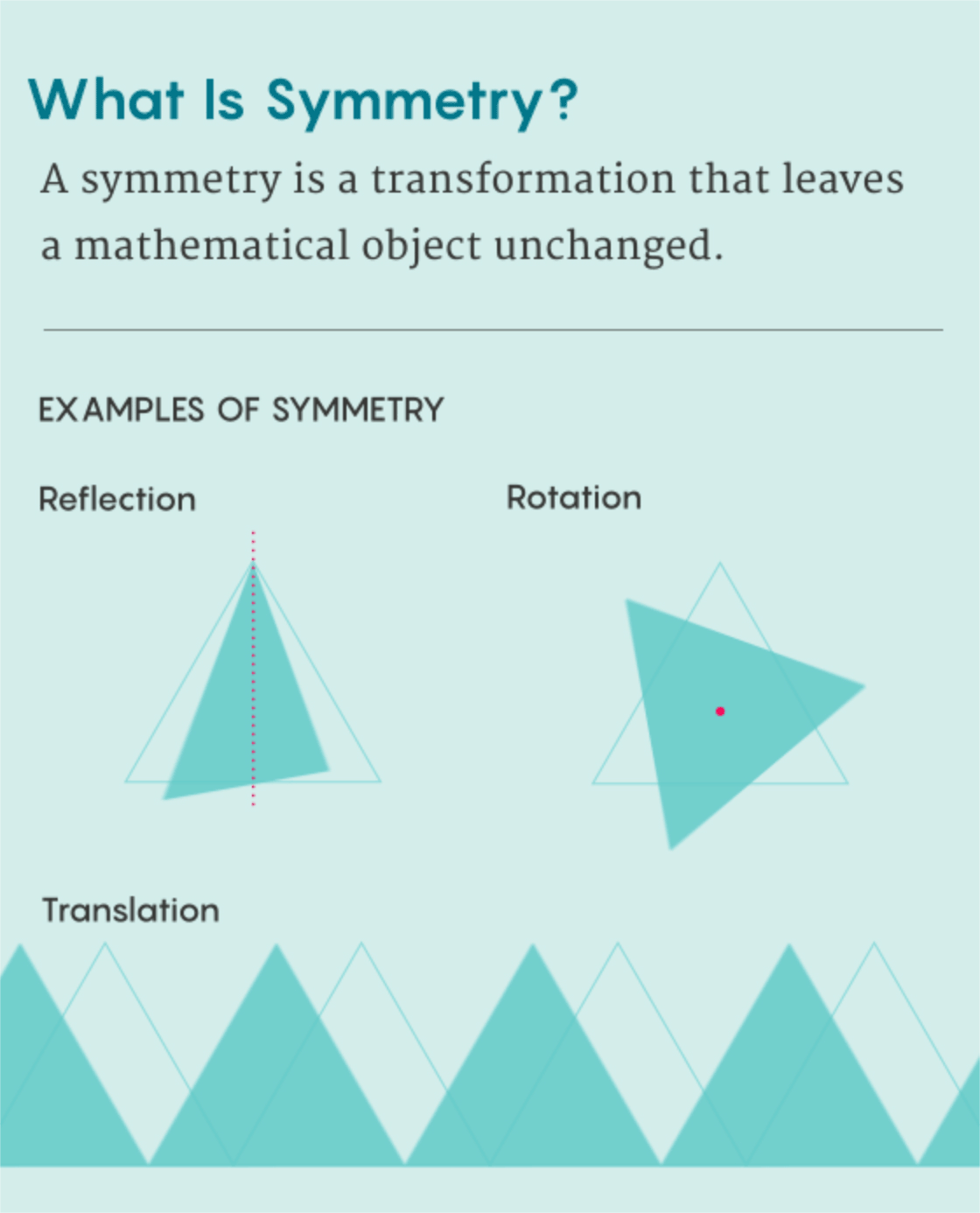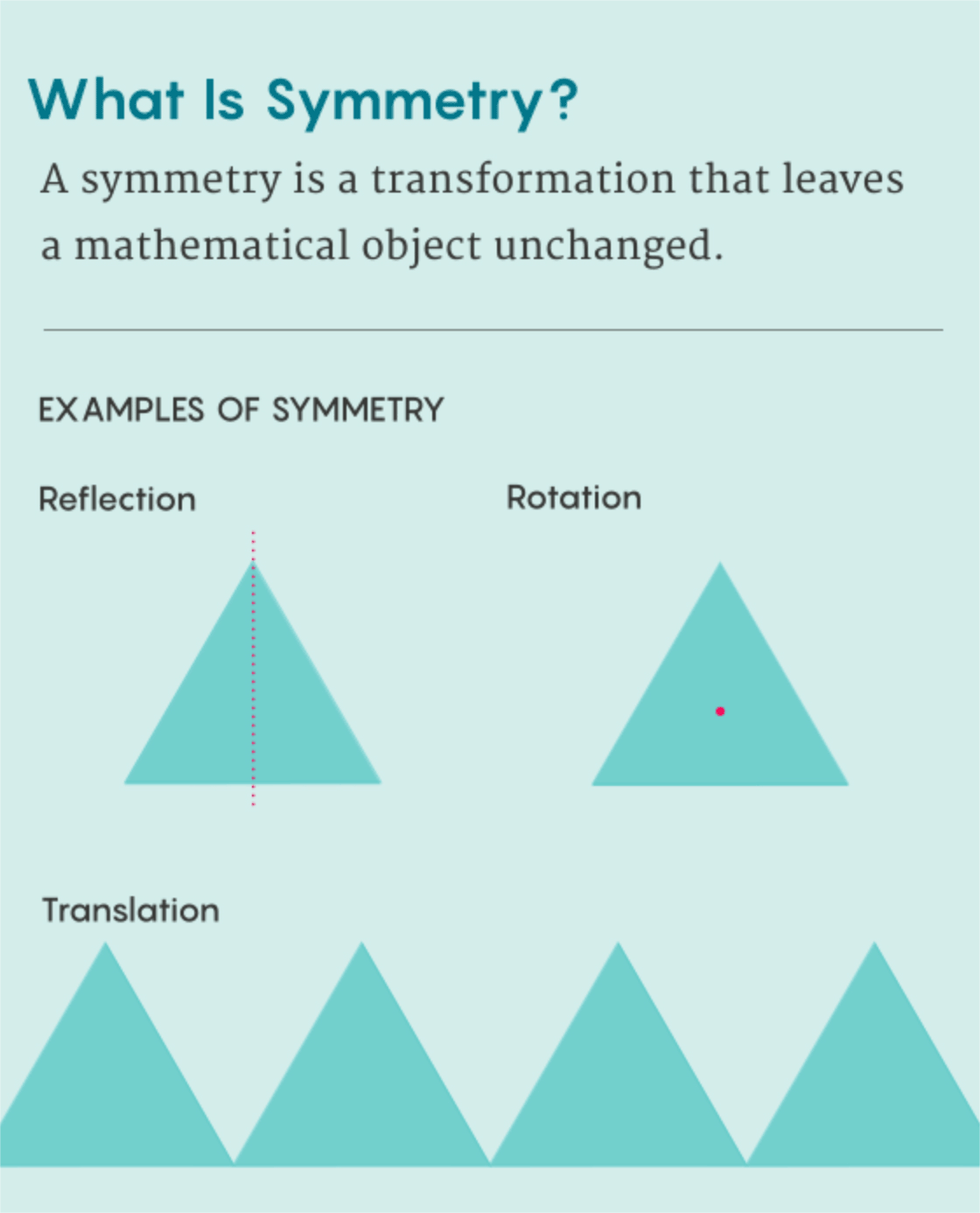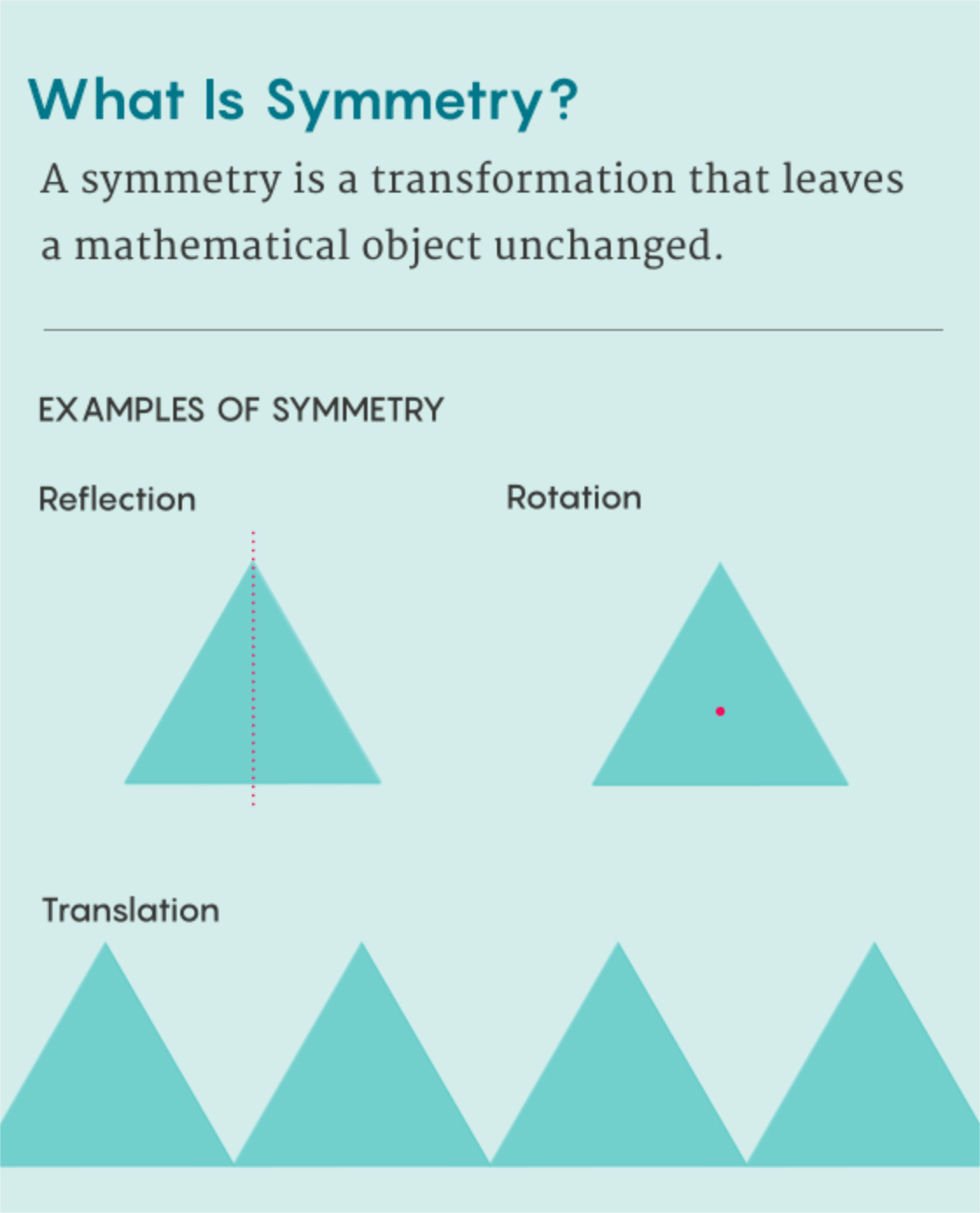
i.e., how many different ways are there that you can pickup, flip, or rotate it around and then set it back down so that it is in the same starting orientation? You get the first transformation by picking up the triangle and setting it back down again unchanged. We’ll call this transformation
.jpg)
Next, if you pickup the triangle and flip it about the vertical axis you get
.jpg)
Aside from the unchanging transformation, each of the transformations is a combination of these two actions. Notice you can multiply any two transformations by first applying one, then the other. In particular, if you multiply any transformation by one, you get the same transformation. This is because one doesn’t actually change the triangle.
.jpg)
This is one way to study a shape in geometry: look at all the ways to transform the shape into itself. These transformations are called symmetries. Believe it or not, there is a close relationship between the of shape and clock arithmetic. Before we see this connection, let’s look at one final example: the integers under addition. Let’s look at a few interesting properties of the integers:
Integers
The integers, which we denote by the letters
Closure: If you add any two integers, you get another integer. We say the integers are closed under addition.
But if you divide one integer by another, you may not get an integer and we say that Integers are not closed under division.
Zero: There’s one number that has a unique property i.e.,
As of now, we have seen three different examples.
Clock arithmetic or modular arithmetic,
Symmetries of a triangle,
Integers
Let’s now see what these three examples all have in common. To begin each of these examples have a set of objects which we call elements.
.jpg)
Elements: For the integer
Operations: For each of these sets, there’s a way to combine any two elements to get another element in the set. We call this an operation, and we use a symbol to show that we are combining two elements. For the integers, the operation is additions and the symbol is a
Clock arithmetic: Subtraction can be rewritten with addition
For example,
.jpg)
Closure: It’s also important to remember that each of the three sets are closed under the operation i.e., if you pick any two elements
Identity: All three structures also have something called identity element, this is an element that has no effect when combined with other elements. For the integers
Inverse: For every elements, there’s an opposite elements which we call the inverse of an element. For the integer under addition, the inverse of
a) For example, the inverse of the element
b) For the integers
There’s one final property that’s essential in the definition of a group i.e., the associative property.
Associativity: This just says that when combining three element, it doesn’t matter how you group them. You can start by combining the first two elements, or you can start with the last two elements. Either way, you’ll end up with the same answer. This in one of those properties people take for granted, but it’s important nonetheless. If grouping did make difference, much of mathematics would come to a screeching halt.
.jpg)
Formal Definition of Group
Let’s now give the general definition of group,
Set of Elements: A Group is a set of elements
Operation: It has an operation which allows you to combine any two elements. Common symbols for the operations are
Closed Under Addition: The group is closed under the operation i.e., if you combine any two elements in the group, you get another element in the group.
Inverse:
Identity: If you combine any element
Associativity: The elements obey the associative property
This is the definition of group. It took mathematicians many years of work to identify these as the most essential properties.
Remarks:
Notice that groups are not required be commutative i.e.,
With the triangle example a flip followed by a rotation gives you something different than a rotation followed by flip.
If a group is commutative, we call it a commutative group. Another common name is an abelian group. If the group is not commutative then we say it’s a non-commutative or non-abelian group.
This definition of group is an abstract idea, but what do you expect from abstract algebra? Because groups are abstract itself, they generalize a lot of different things from arithmetic, algebra, geometry an more. This generality is what makes groups so powerful. The mathematics you learn in abstract algebra can be applied to many different subjects.
Arithmetic
To get things started, let’s think back to arithmetic. When studying arithmetic, you learn how to add, subtract, multiply, and divide different kinds of numbers: integer, fractions, real numbers, complex number. Then one day, probably when you least expected it, you learned that subtraction is addition in disguise! For example,
In abstract algebra, we use the word “inverse” instead of “opposite”. If you combine a number with its inverse, you get an identity element. For addition, identity is
Textbook Definition of Group
A group is a set of elements.
The group has one operation
Closed under
Inverses
Identity:
Associativity Property
Remarks
Notice we’ve claimed “elements” instead of “numbers”, because ‘Element’ is more abstract.
If you combine two elements in the group, the results is also in the group.
Each element has an inverse.
If you combine an element with its inverse, you get an element we call an identity element.
The associativity property is a very important property because without this property you can not solve any equations.

Groups: Motivation For The Definition
After reading this formal definition one can definitely ask that why these rules and what’s so special about these properties? I would like to motivate this definition with a simple example.
Imagine that we were asked to define a group. Specifically, we want to define a group for a integers under addition. We want our definition to be as simple as possible the simpler the better. One thing we would like to be able to do is solve basic equations. If we’re going to generalize algebra, if we’re going to be abstract algebra, then we need to be able to solve equations. So let’s solve an equation
Solve The Equation
Methodology
First we add

So it turns out that the definition of a group is the simplest definition that will let you solve a basic equation.
The Definition of a Subgroup
Suppose we have a group which we call
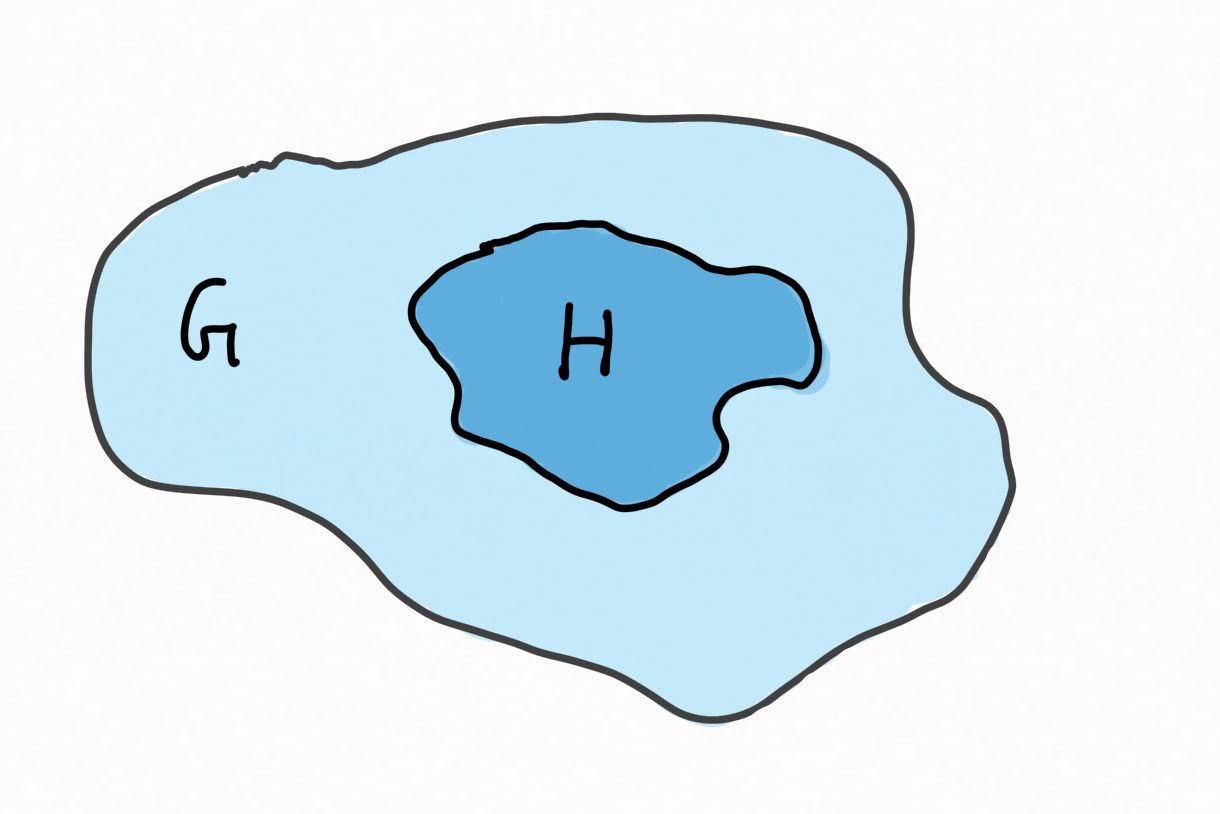
To avoid writing words there’s a math symbol used to indicate the
Technical Postscript
Technically
Group Multiplication Tables
When you learned arithmetic you probably had to memorize a multiplication table. The table below shows you how to multiply any two small numbers usually the integers
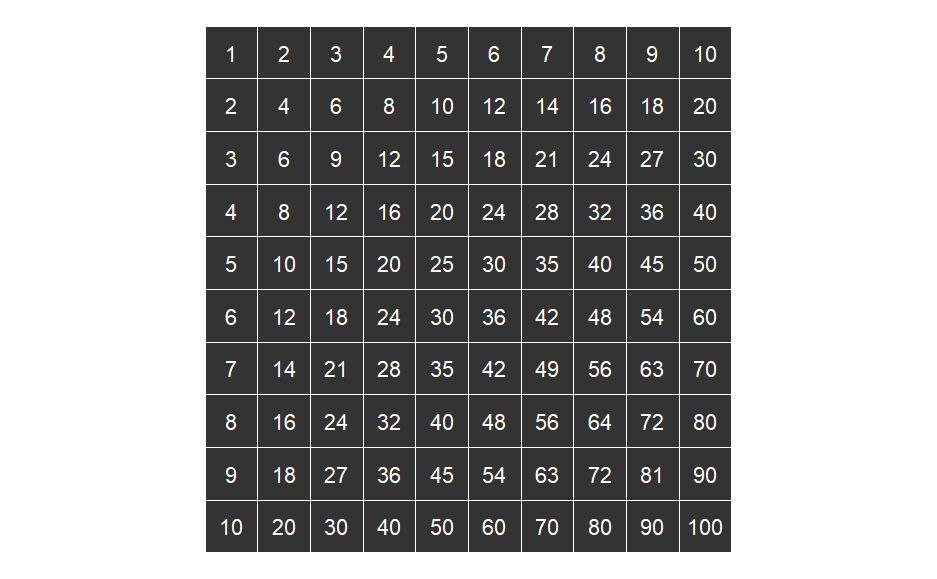
In abstract algebra, you begin to work with new types of numbers. Groups behave very differently than the numbers in arithmetic. So when you’re first starting out in abstract algebra, it’s helpful to go back to the basics and make a group multiplication