The Quest for Precision Along Coastal Edges
Measuring Nature’s Symphony
Coastlines taunt us with their infinite intricacies, challenging our notions of length and limit, and inviting us to embrace the enigma of their paradoxical existence.
Capturing Nature’s Wild Canvas
Imagine standing at the edge of the ocean, where land and sea intertwine in a mesmerizing display of natural artistry. With each wave and gust, the landscape shifts, eroding and reshaping in a perpetual dance. The coastline stretches before you, its rugged contours etched by the relentless forces of wind and water. Attempting to quantify this untamed beauty encounters a fundamental hurdle—the very units we employ to measure it. There are no straight lines, no smooth curves—only the wild, untamed beauty of nature.
With each passing wave, the coastline evolves, eroding cliffs and carving new coves. It’s a dynamic landscape, ever-changing and impossible to pin down with traditional measurements. In this realm where precision meets the unpredictable, our attempts to measure the coastline are like trying to capture the wind in a net. The challenge lies not only in the intricacies of nature’s design but also in the very units we use to quantify it. Nature defies our efforts to impose order, reminding us of its boundless creativity and eternal mystery
Nature’s artistry knows no bounds along the coastlines, where the elements choreograph a symphony of irregularity.
Coastlines, the dynamic meeting points of land and sea, defy the notion of uniformity with their irregular contours shaped by the relentless forces of nature. Devoid of straight lines or gentle curves, they continuously evolve, making measurement a formidable challenge. At the heart of this complexity lies the very unit we use to quantify them, presenting a significant obstacle in our quest to understand and delineate these captivating landscapes.
A Journey into Coastal Measurement Challenges
Let’s embark on a journey of discovery along the captivating coastlines, where the enigmatic forces of nature weave their intricate tapestry. Imagine traversing the shores of New Guinea, a breathtaking island surrounded by the endless expanse of the sea. As we venture forth, armed with our measuring tools and a sense of curiosity, we encounter a puzzling conundrum. Initially, our attempt to quantify the coastline with units roughly \(500 \ \text{Km}\) in length reveals a stark reality—it’s far from accurate. Despite our efforts, we find ourselves with a total measurement of \(3000\ \text{Km}\), a mere approximation of the true expanse. Undeterred by the initial setback, we decide to refine our approach. Halving the size of our units and retracing our steps, we anticipate a more precise outcome. While the results appear promising, with a measured coast line of \(3750\ \text{Km}\), the elusive nature of accuracy still eludes us. With determination driving us forward, we continue to iterate, halving the unit size once more. Each attempt brings us closer to our goal, yet the coastline continues to unveil its complexity. Even with units reduced to their smallest scale, yielding a measurement of \(4125\ \text{Km}\), perfection remains just out of reach. In our quest for precision, we are reminded of the intricacies of nature’s design.
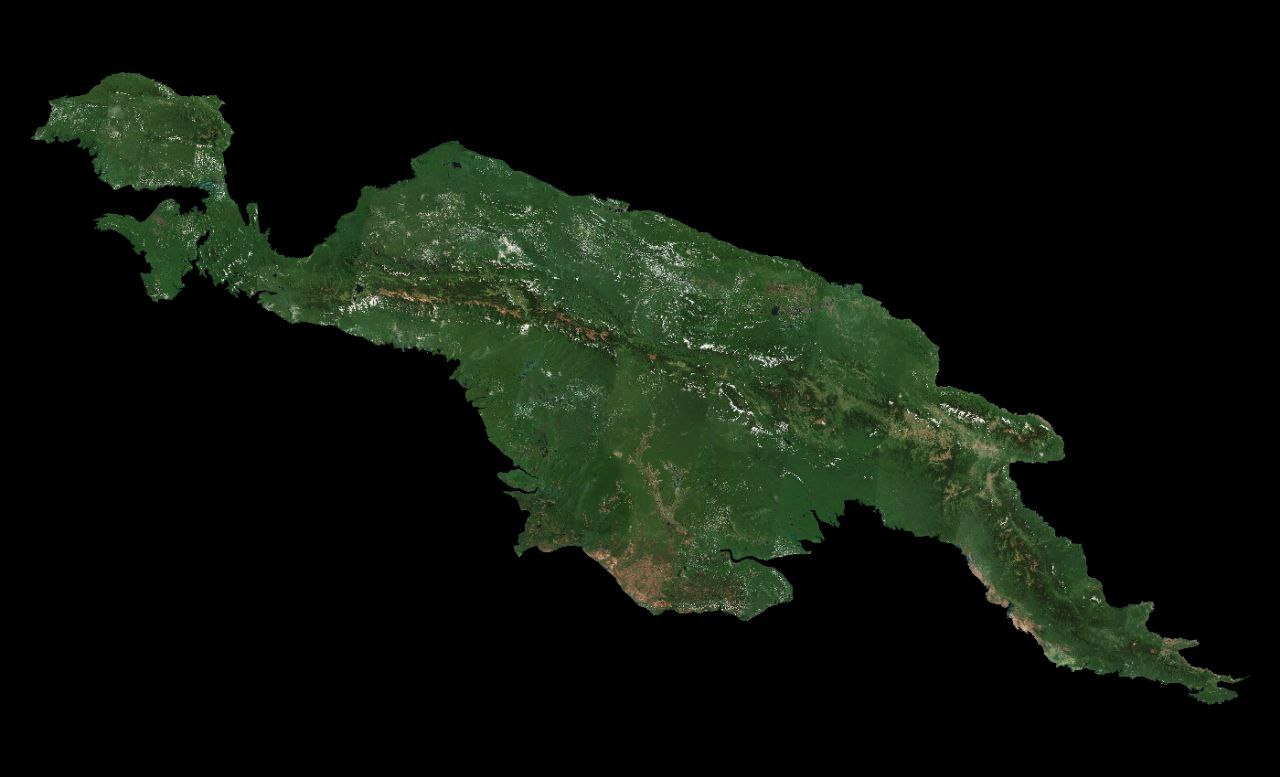
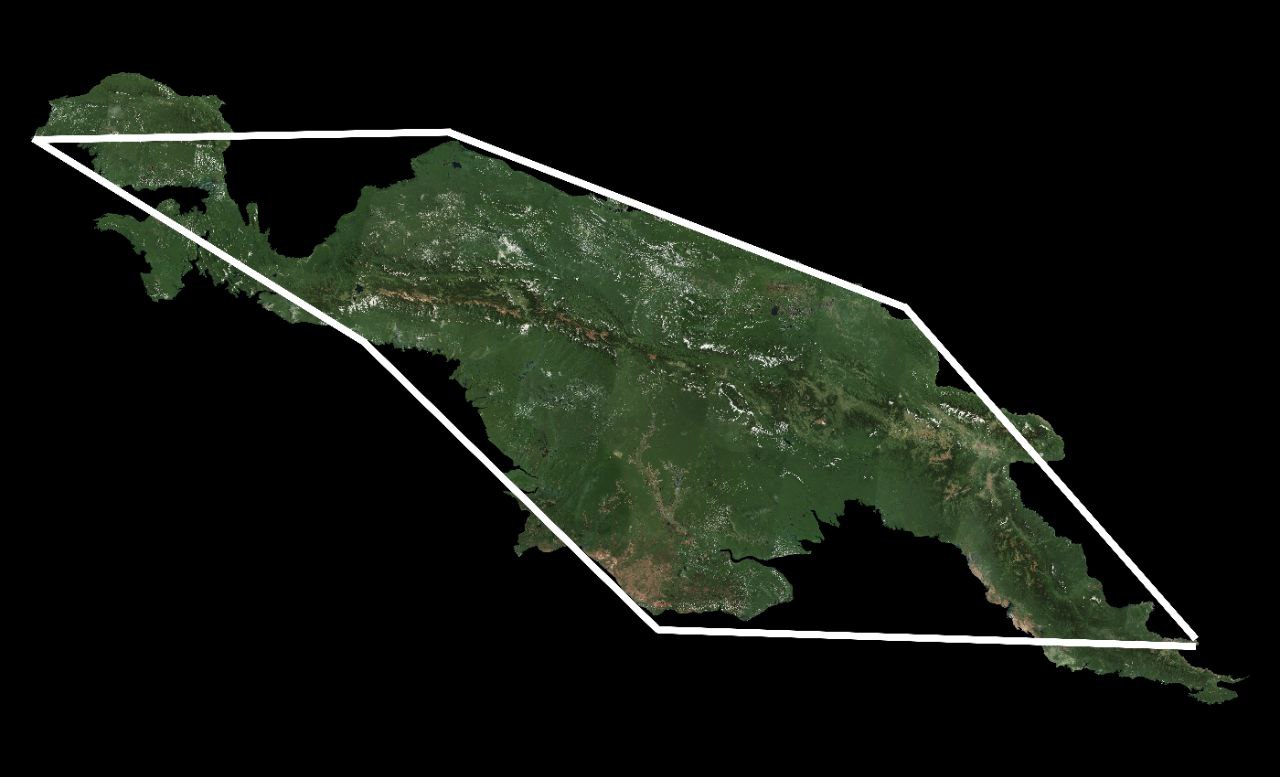
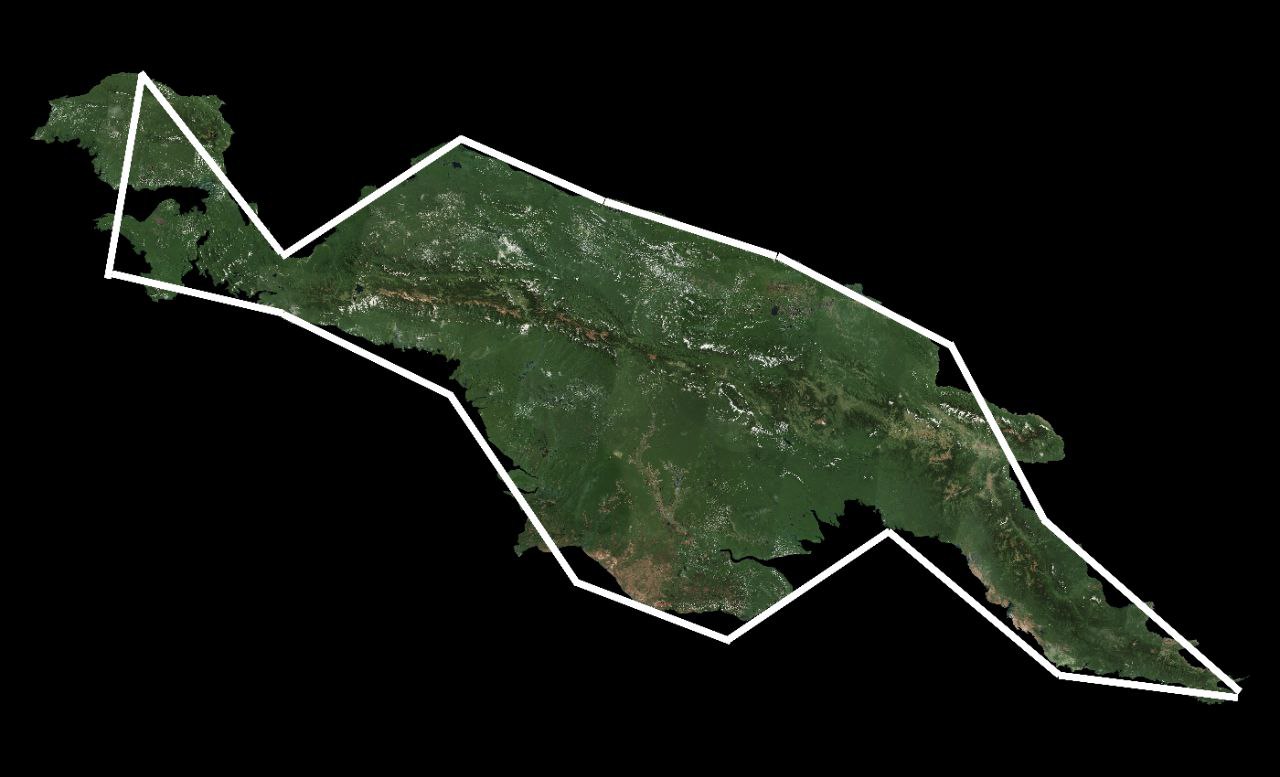
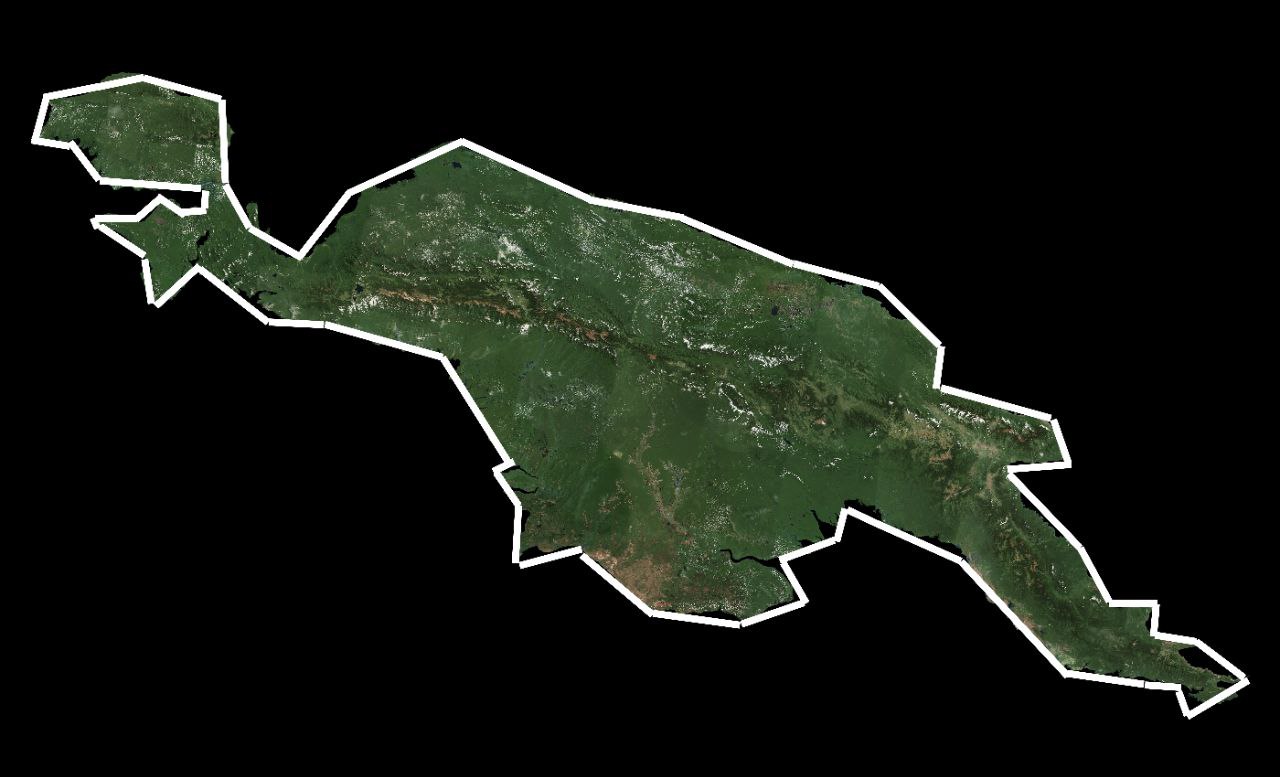
The coastline, with its ever-changing contours and subtle nuances, defies our attempts to neatly quantify its majesty. Despite our best efforts, we find solace in the journey itself—a testament to the boundless creativity and eternal mystery that characterize our world’s coastal wonders. You’re noticing the trend by now with each smaller unit of measurement the larger our measurement becomes. This happens because closer you look the more intricate the coastline becomes that increased complexity means more coastline to measure.
The Intriguing Coastline Paradox
Dive into the fascinating world of coastline measurement, where this perplexing phenomenon known as the Coastline Paradox reigns supreme. Discovered by the astute mathematician Lewis Fry Richardson in 1951, this paradox illuminates the subjective nature of determining coastline lengths.
Picture this: two neighboring countries, Portugal and Spain, attempting to delineate their mutual border. Surprisingly, their measurements yield vastly different results—a conundrum attributed to the coastline paradox.
So, what exactly is this paradox? Simply put, the length of a coastline varies depending on the size of the measurement unit used. The smaller the unit, the longer the coastline appears. In theory, one could even use molecular-level units, resulting in a coastline length that seems to stretch to infinity.
Imagine applying this concept to the beautiful island of New Guinea. Despite its finite area, if measured with infinitesimally small units, its coastline would seemingly extend endlessly—a mind-boggling notion that challenges our understanding of spatial boundaries. We unravel the enigmatic Coastline Paradox, delving into its implications for cartographers and exploring the philosophical questions it raises about the nature of space and measurement.
You could, theoretically, go all the way down to the molecular level for your measurement unit. But if you do that, the length of the coast seems to approach infinity. It doesn’t seem to make any sense that you can have a defined space with a finite area like New Guinea be surrounded by an infinitely long perimeter.
The Fascinating World of the Koch Snowflake
There is a similar concept that can be found in mathematics called fractals. It’s almost like measuring a fractal where the closer you look the more there is to see indefinitely. Enter the mesmerizing realm of fractals, a captivating concept from the world of mathematics.
Picture a simple triangle, its sides all equal to one. Now, imagine adding smaller triangles to each side, each with lengths one-third of the original (See, Fig. 2.1 & 2.2). This process can go on indefinitely, creating intricate patterns that seem to stretch endlessly. One of the most iconic examples is the Koch Snowflake—a mesmerizing shape that, when you zoom in, reveals an endless maze of intricate detail (See, Fig. 2.3 , 2.4, 2.5). But here’s where it gets truly mind-bending: despite its infinite complexity, when you zoom back out to the original starting point, you’re left with a shape that has a finite area. Yet, its perimeter stretches on infinitely—a paradoxical notion that challenges our understanding of space and dimension.
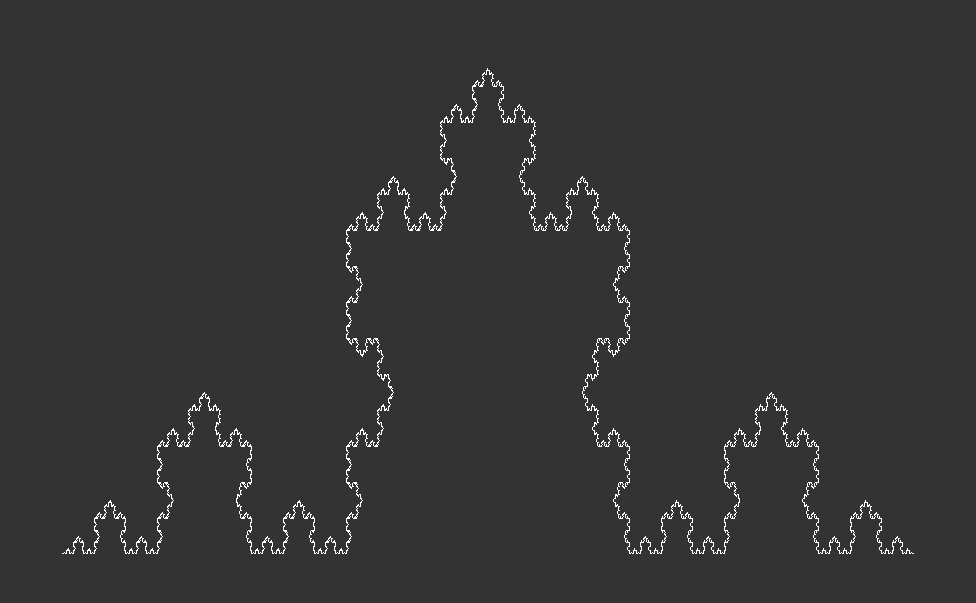
Beyond the Horizon
A lot of coastlines across the world has similar properties to this. So you can keep zooming in and zooming in on the coast of New Guinea and coastline will continue to look roughly the same. No matter how far down the rabbit hole you go as mentioned previously, you’ll eventually hit the molecule level, if you zoom in far enough and you’ll be measuring a beach by counting atoms. If you did this forever, you’d find the coast of New Guinea to be probably millions of kilometers in length which, just isn’t very practical or easy to understand.
Even as we delve deeper, down to the molecular level, measuring the coastline presents its own set of challenges. Attempting to measure the distance between atoms reveals the inherent complexity of this task, with the measurement seemingly approaching infinity.
Coastline Conundrums
Now we need to take a step back and remember that the sea is not static, the tide comes in and goes out and simultaneously goes out and comes in on the other side of the world twice everyday. The coastline even varies a second to second as waves crash on shores and then recede. Each wave moves the sands and erodes parts of the beach, physically changing what the coastline is which might seem small until you remember we need to use as small of a unit as possible to get the most accurate measurement. Even if we could freeze the ocean or just take the average between the high and low tides, we’d still have issues like the ‘River Problem’.
The river problem i.e., where exactly does a river end and the ocean begin. If you see the picture’s below you might confuse which is the actual coastline.
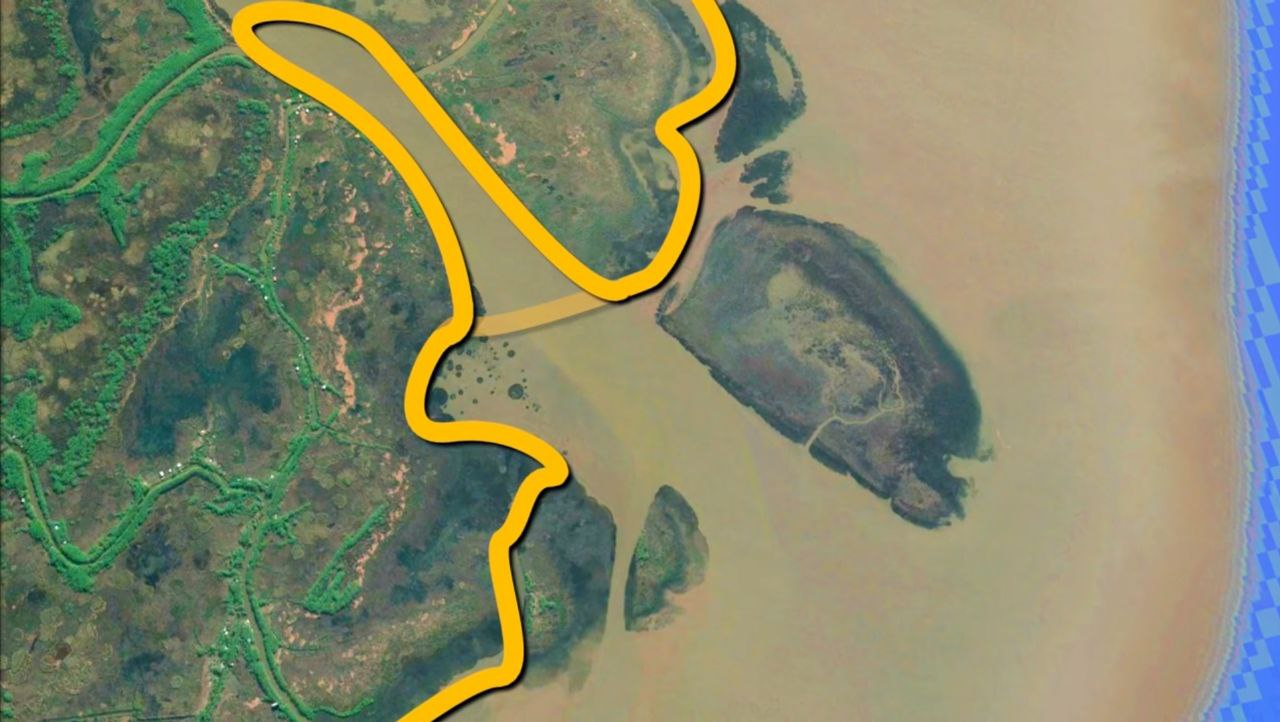
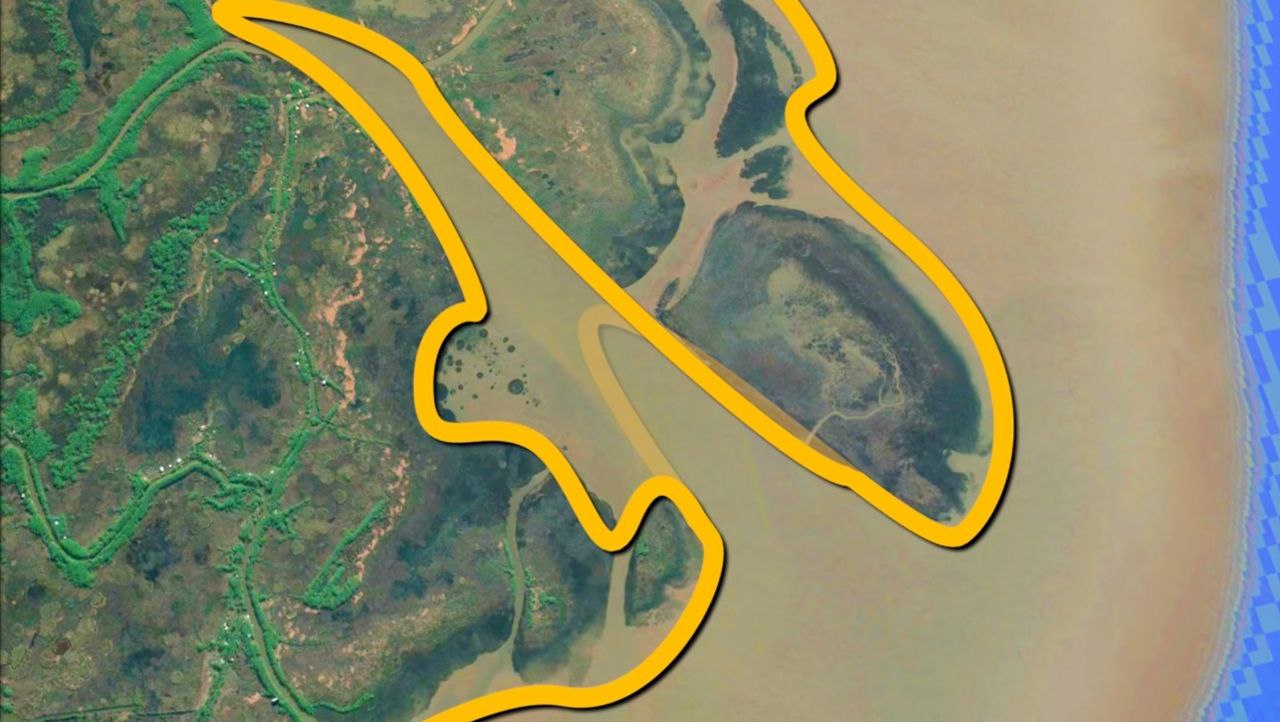
In the grand scheme of things, the nuances of coastline measurement might seem trivial. However, when faced with intricate coastlines like the one depicted in figure below, these details become significant challenges.
Consider the finer points: where precisely does the land transition to water? How moist does the sand need to be before it’s classified as part of the ocean? And what about lakes? Do they contribute to a country’s coastline?
These questions may appear trivial at first glance, but they spark lively debates among geographers. The boundary between land and water isn’t always clear-cut, and defining it accurately can have far-reaching implications. The meticulous world of coastline delineation, exploring the intricacies of defining land-sea boundaries and uncovering the complexities that lie beneath the surface. It’s a journey that promises to challenge our perceptions and shed light on the subtle interplay between land, water, and geography.
Mathematical Aspects Behind Coastal Measurement
Approaching to Measure
The usual way to figure out how long a border (or coastline) is was to use a ruler on a map or photo. You’d lay down n straight-line parts, each of length \(l\), so that they all fit along the border. Lewis Fry Richardson checked this method and found something strange. He noticed that if you make the ruler shorter, the total length of the segments gets bigger. So, if you use a shorter ruler, you’ll measure a longer border. It turned out that Spanish and Portuguese geographers were using rulers of different lengths. The weirdest part for Richardson was that when the length of the ruler (\(l\)) gets closer and closer to zero, the length of the coastline seems to go on forever. Richardson thought that, like regular shapes, coastlines would have a fixed length.
For example, the more sides you add to a polygon inside a circle, the closer its perimeter gets to the circle’s circumference (and the shorter each side gets). In math terms, a smooth curve like a circle that you can break down into small straight parts with a definite limit is called a “rectifiable curve.” Benoit Mandelbrot later showed that a number called “\(D\)” doesn’t change, no matter how small you make the parts (\(\epsilon\)).
The concept of length stems from Euclidean distance, where a straight line is the shortest distance between two points, having one consistent length. However, on a spherical surface, this is replaced by geodesic length, measured along the curve that exists on the plane containing both endpoints and the center of the sphere.
Idealized Fractals
Calculating the length of curves becomes more complex, but approximations can be made by summing the lengths of straight lines connecting points. Using more numerous and shorter lines yields estimates closer to the true length of the curve. Calculus enables precise length calculations, handling infinitesimally small distances.
Smooth curves can be assigned precise lengths, as illustrated in animations. Yet, not all curves can be measured this way. Fractals, with changing complexity based on measurement scale, diverge in measured length as precision increases. This divergence leads to infinite length, especially evident when measuring coastlines with near-infinite resolution.
However, this assumes space can be infinitely subdivided—a philosophical notion underlying Euclidean geometry. Coastlines, unlike idealized fractals, lack definite construction as they’re shaped by random natural events rather than formulaic sequences.
Benoit Mandelbrot Work & Fractal Geometry
After Richardson’s work, Mandelbrot introduced fractal geometry—a new kind of math to understand complex natural shapes like coastlines. He named these shapes “fractals” from the Latin word “fractus,” meaning irregular fragments. Mandelbrot’s \(1967\) paper explored curves that repeat themselves at different scales, calling them self-similar curves. He found that when you measure coastlines with smaller tools, the length seems to keep increasing without limit. This happens because coastlines are so curvy. Mandelbrot showed how these curves, like the Koch snowflake, can be calculated using the Hausdorff dimension, which falls between \(1\) and \(2\).
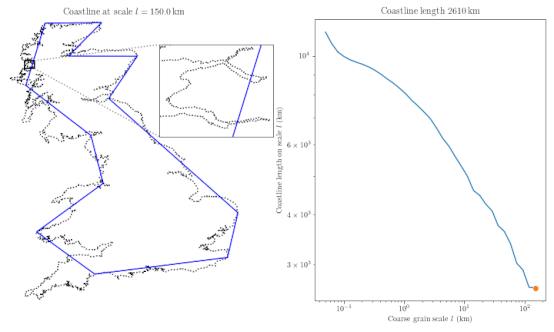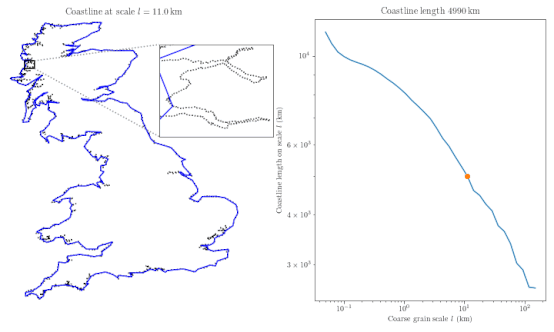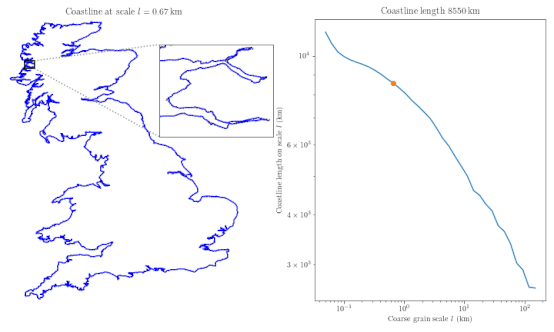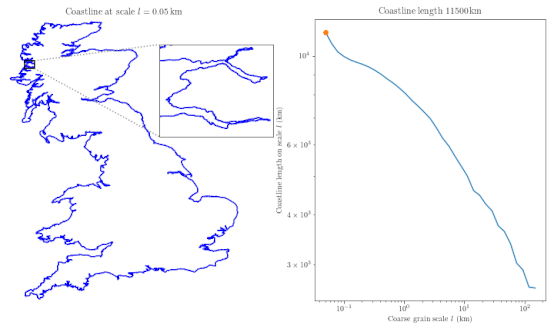
One big idea from Mandelbrot’s work is that coastlines can be modeled as self-similar shapes, meaning they look similar no matter how much you zoom in. This property makes measuring coastline length tricky—it’s like trying to grab onto something slippery. Mandelbrot’s work extended Richardson’s ideas, introducing a parameter called \(D\), representing the fractal dimension. This dimension helps measure the complexity of coastlines, with higher values indicating more intricate shapes. For example, South Africa’s coastline has a D value of about \(1.02\), while the west coast of Great Britain has a value of approximately \(1.25\).
Solutions & Implementations
The coastline paradox presents a real-world challenge with significant implications. To address this issue, various solutions have been suggested. These solutions aim to define the term “coastline,” establish practical physical boundaries for coastlines, and employ mathematical principles within these boundaries to calculate lengths with meaningful precision. By defining what constitutes a coastline and determining its physical limitations, practical solutions can be devised to accurately measure its length. These approaches enable the resolution of the problem in real-world applications, ensuring that measurements align with practical needs and constraints.
While these practical solutions effectively address the issue in real-world scenarios, the coastline paradox remains a theoretical and mathematical concept within our models. Despite this theoretical complexity, practical applications can proceed with confidence, thanks to the implementation of these solutions.
Controversies & Criticism
The coastline paradox has faced criticism because coastlines, being tangible and finite geographical features, should theoretically have a quantifiable length. While comparing coastlines to fractals is helpful in illustrating the issue, it’s deemed inaccurate since coastlines lack the self-repeating nature of true fractals and are inherently finite. The root of the paradox lies in how we measure reality, particularly when trying to translate those measurements into cartographic models of coastlines. Despite advancements in technology like LiDAR, GPS, and GIS, which have eased the process, challenges persist due to limitations in survey measurements and vector software. Critics argue that these challenges are more theoretical and less practical concerns for planners and cartographers.
Conclusion
In the grand scheme of things, the nuances of coastline measurement might seem trivial. In this pursuit of understanding, we find ourselves confronting the complexities of fractals and the Coastline Paradox, where the act of measurement itself becomes an intricate dance between precision and uncertainty. Indeed, measuring a coastline is more than just determining its length—it’s a journey into the depths of mathematical and philosophical inquiry.
References
Mandelbrot, B. (1967). “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension” (PDF). Science. 156 (3775): 636–638. doi:10.1126/science.156.3775.636. PMID 17837158. S2CID 15662830.
Steinhaus, Hugo (1954). “Length, shape and area”. Colloquium Mathematicum. 3 (1): 1–13. doi:10.4064/cm-3-1-1-13. The left bank of the Vistula, when measured with increased precision would furnish lengths ten, hundred and even thousand times as great as the length read off the school map. A statement nearly adequate to reality would be to call most arcs encountered in nature not rectifiable.
Vulpiani, Angelo (2014). “Lewis Fry Richardson: scientist, visionary and pacifist”. Lettera Matematica. 2 (3): 121–128. doi:10.1007/s40329-014-0063-z. MR 3344519. S2CID 128975381.
Seekell, D.; Cael, B.; Lindmark, E.; Byström, P. (2021). “The Fractal Scaling Relationship for River Inlets to Lakes”. Geophysical Research Letters. 48 (9): e2021GL093366. doi:10.1029/2021GL093366. S2CID 235508504.