The Enigmatic World of Fractals

Exploring Local Connectivity and Infinite Complexity in the Mandelbrot and Julia Sets

Mathematics
Author

Abhirup Moitra

Published

June 12, 2024

Exploring the Mandelbrot and Julia sets is like peering into infinity; each zoom reveals an ever-deeper world of intricate beauty and boundless complexity, where mathematics meets art in a dance of eternal fascination.

Voyage Through The World of Fractals

Behold, this infinite mathematical universe. A dizzying cascade of fractals. Arrays of complex patterns filled with both satisfying self-similarity and surprising, novel features. Each iteration delves deeper into a realm where order and chaos intertwine, revealing intricate structures that defy our intuition.

All of the structure and the patterns that you see there really do exist for a reason. There is some sort of innate mathematical cause behind all of the phenomena that you see. ~ Alex Kapiamba (Mathematician, Brown University)

Code 
def mandelbrot(x, y, threshold):
    """Calculates whether the number c = x + i*y belongs to the 
    Mandelbrot set. In order to belong, the sequence z[i + 1] = z[i]**2 + c
    must not diverge after 'threshold' number of steps. The sequence diverges
    if the absolute value of z[i+1] is greater than 4.
    
    :param float x: the x component of the initial complex number
    :param float y: the y component of the initial complex number
    :param int threshold: the number of iterations to considered it converged
    """
    # initial conditions
    c = complex(x, y)
    z = complex(0, 0)
    
    for i in range(threshold):
        z = z**2 + c
        if abs(z) > 4.:  # it diverged
            return i
        
    return threshold - 1  # it didn't diverge
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

x_start, y_start = -2, -1.5  # an interesting region starts here
width, height = 3, 3  # for 3 units up and right
density_per_unit = 250  # how many pixles per unit

# real and imaginary axis
re = np.linspace(x_start, x_start + width, width * density_per_unit )
im = np.linspace(y_start, y_start + height, height * density_per_unit)

fig = plt.figure(figsize=(10, 10))  # instantiate a figure to draw
ax = plt.axes()  # create an axes object

def animate(i):
    ax.clear()  # clear axes object
    ax.set_xticks([], [])  # clear x-axis ticks
    ax.set_yticks([], [])  # clear y-axis ticks
    
    X = np.empty((len(re), len(im)))  # re-initialize the array-like image
    threshold = round(1.15**(i + 1))  # calculate the current threshold
    
    # iterations for the current threshold
    for i in range(len(re)):
        for j in range(len(im)):
            X[i, j] = mandelbrot(re[i], im[j], threshold)
    
    # associate colors to the iterations with an iterpolation
    img = ax.imshow(X.T, interpolation="bicubic", cmap='magma')
    return [img]
 
anim = animation.FuncAnimation(fig, animate, frames=45, interval=120, blit=True)
anim.save('mandelbrot.gif',writer='imagemagick')

This is the Mandelbrot Set. These trippy images represent a form of modern algorithmic exploration, one made possible by computers. A handful of mathematicians have devoted their lives uncovering this set’s secrets.

It plays a very central role in our understanding of much more complicated systems. It’s step number one ~ Laura Demarco (Mathematician, Havard)

From the mesmerizing beauty of the Mandelbrot set to the delicate intricacies of Julia sets, these fractals embody the essence of mathematical elegance and complexity. As we explore their boundless depths, we uncover not just shapes and patterns, but the fundamental principles governing dynamical systems, chaos theory, and the very fabric of mathematical reality. This journey through fractals is a testament to the power and beauty of mathematics, offering endless avenues for discovery and inspiration.

Studying of Mandelbrot Set

Code 
import numpy as np 
import matplotlib.pyplot as plt 
plt.style.use('dark_background')

def mandelbrot_set(h_range, w_range, max_iterations):
    y, x = np.ogrid[-1.4: 1.4: h_range*1j, -1.8: 1: w_range*1j]
    a_array = x + y*1j
    z_array = np.zeros(a_array.shape, dtype=complex)  # Initialize z_array with dtype complex
    iterations_till_divergence = np.zeros(a_array.shape, dtype=int)  # Initialize as integers
    for h in range(h_range):
        for w in range(w_range):
            z = z_array[h][w]
            a = a_array[h][w]
            for i in range(max_iterations):
                z = z**2 + a
                if z * np.conj(z) > 4:
                    iterations_till_divergence[h][w] = i
                    break
    return iterations_till_divergence

plt.imshow(mandelbrot_set(800, 800, 30), cmap='twilight_shifted')
plt.axis('off')
plt.show()
plt.close()

#_____________________________________________________________________________
import numpy as np 
import matplotlib.pyplot as plt 
plt.style.use('dark_background')


def mandelbrot_set(h_range, w_range, max_iterations):
    # top left to bottom right
    y, x = np.ogrid[1.4: -1.4: h_range*1j, -1.8: 1: w_range*1j]
    a_array = x + y*1j
    z_array = np.zeros(a_array.shape)
    iterations_till_divergence = max_iterations + np.zeros(a_array.shape)

    for i in range(max_iterations):
        # mandelbrot equation
        z_array = z_array**2 + a_array

        # make a boolean array for diverging indicies of z_array
        z_size_array = z_array * np.conj(z_array)
        divergent_array = z_size_array > 4

        iterations_till_divergence[divergent_array] = i

        # prevent overflow (numbers -> infinity) for diverging locations
        z_array[divergent_array] = 0 
    
    return iterations_till_divergence

plt.imshow(mandelbrot_set(2000, 2000, 70), cmap='twilight_shifted')
plt.axis('off')
plt.savefig('mandelbrot.png', dpi=300)
plt.close()

The Mandelbrot set is a perfect example of how a simple rule can produce incredible complexity. At it’s core the set is generated by iterating a quadratic equation, \(f(z) = z^2 +c\), a simple formula whose highest exponent is \(2\). To iterate a quadratic equation, choose a value for the variable, plug it into the function, then take the output and feed it back in again and again. The study of how recursive functions like these changes over time is central to a field of math called ‘Complex Dynamical Systems’.

This subject emerged to comprehend the tangible world. What mathematical principles underlie the physical realities we observe? One of the earliest and most crucial examples is the solar system. We delve into dynamical systems, where a set of rules governs the evolution of a space over time, determining the movements and transformations within it.

Starting From The Root

Consider, for instance, the simple function \(f(z)=z+1.\) In this context, we start with an initial value of \(z\)and evaluate the function. The result is then used as the new input parameter, and the function is evaluated again. This iterative process can be formally described as follows:

  1. Start with an initial value \(z_0\)​.

  2. Compute \(z_1​=f(z_0​)=z_0​+1.\)

  3. Use \(z_1\) as the new input to compute \(z_2​=f(z_1​)=z_1​+1\), and so forth.

Mathematically, this generates a sequence \(\{z_n\}\) where \(z_{n+1}​=f(z_n​)=z_{n​}+1.\) This sequence clearly grows without bound, illustrating a simple yet profound example of iterative processes in dynamical systems. Such iterations lay the groundwork for understanding more complex functions and their behaviors, which ultimately lead to the rich, intricate patterns observed in fractals.

Finally we’ll see that,

\[ f(0) = 0+1 =1 \]

\[ f(1) = 1+1 = 2 \]

\[ f(2) = 2+1 =3 \]

\[ \text{and so on}\ldots \]

The pattern here is straightforward: we evaluate the function, use the result as the new input, and re-evaluate the function. In this simple case, observing the pattern is easy, as the value increases by one with each iteration. While this example is quite basic, Mandelbrot extended this concept significantly further.

Mandelbrot studied the function \(f(z)=z^2+c\). To illustrate this with a simple example, let’s choose \(c=1\). Therefore,

\[ f(0) =1 \]

\[ f(1) =2 \]

\[ f(2) = 5 \]

\[ f(5) = 26 \]

It becomes apparent that the values will rapidly spiral out of control this time and diverge to infinity. Now let’s try plugging in \(-2\). Therefore,

\[ f(0) = -2 \]

\[ f(-2) = 2 \]

\[ f(2) =2 \]

This process will continually yield the value \(2\). By repeatedly evaluating \(f(2)\) and obtaining \(2\), this iteration continues indefinitely. Consequently, this indicates that \(-2\) lies on the boundary of the Mandelbrot set. To visualize this concept, let’s draw a number line.

Code 
# Create a sequence of numbers from -10 to 10
numbers <- -2:2

# Include the additional point 1/4
additional_point <- 1/4

# Plot the number line
plot(numbers, rep(0, length(numbers)), type = "n", xlab = "Number Line", 
                                                   ylab = "", 
                                                   yaxt = "n", 
                                                   bty = "n", 
                                                   main = "Number Line")

# Add points to the number line
points(numbers, rep(0, length(numbers)), pch = 16)

# Add the additional point
points(additional_point, 0, pch = 16, col = "red")

# Add labels below the points
text(numbers, rep(-0.1, length(numbers)), labels = as.character(numbers), 
                                          cex = 0.8)

# Add label for the additional point
text(additional_point, -0.1, labels = "1/4", col = "red", cex = 0.8)

# Draw a horizontal line to represent the number line
abline(h = 0, col = "black")

# Add arrows at the ends of the number line
arrows(-10, 0, 10, 0, length = 0.1, code = 3)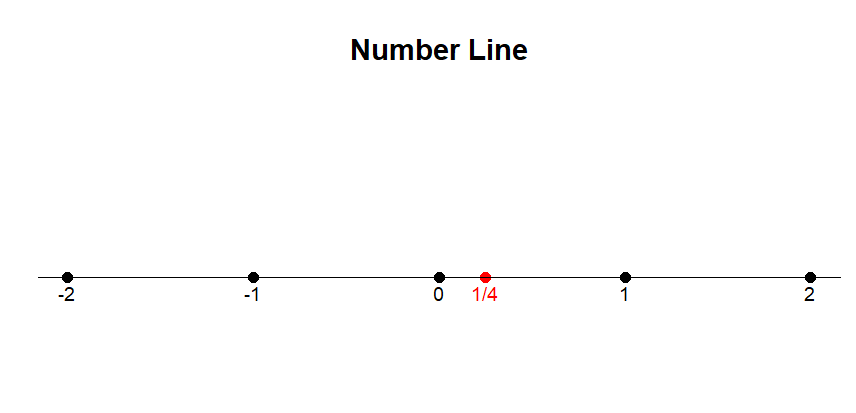

Here, \(-2\) represents the largest magnitude that remains bounded and does not diverge to infinity when iterated from \(0.\)

Let’s try plugging, \(c= -2.1\). Therefore,

\[ f(0) = 0^2 - 2.1 = -2.1 \]

\[ f(-2.1) = (-2.1)^2 -2.1 = 2.41 \]

\[ f(2.41) = (2.41)^2- 2.1 = 3.81 \]

\[ f(3.81) = (3.81)^2 -2.1 =12.5 \]

Consider the parameter \(c=−2.1.\) Through successive iterations of the function \(f(z)=z^2+c\), we embark on a journey: \(-2.1, 2.41, 3.81, 12.5\), and so forth, each value exponentially greater than the last. This vividly illustrates that the Mandelbrot set’s boundary is encapsulated by \(-2\), beyond which values spiral into infinity.

Now, let’s shift our focus to the positive boundary. Surprisingly, it resides at \(c=\frac{1}{4}\), a less intuitive revelation. When we substitute \(\frac{1}{4}\) for \(c\), the sequence inches closer and closer to \(\frac{1}{2}​\), but never quite reaches it. Any departure beyond \(\frac{1}{4}\) propels the sequence into an unbounded trajectory towards infinity.

We may visually represent this by shading the region between these two values on a number line, symbolizing the real numbers encompassed by the Mandelbrot set. The interval stretches from \(-2\) to \(\frac{1}{4}\)​, delineating the scope of this fractal phenomenon. At this juncture, some individuals might conclude their exploration. However, what follows promises a journey into deeper complexity.

Code 
# Create a sequence of numbers from -2 to 2
numbers <- -2:2

# Include the additional point 1/4
additional_point <- 1/4

# Plot the number line
plot(numbers, rep(0, length(numbers)), type = "n", xlab = "Number Line", 
                                                   ylab = "", 
                                                   yaxt = "n", 
                                                   bty = "n", 
                                                   main = "Number Line")

# Add a shaded region between -2 and 0
rect(-2, -0.05, 0, 0.05, col = "yellow", border = NA)

# Add points to the number line
points(numbers, rep(0, length(numbers)), pch = 16)

# Add the additional point
points(additional_point, 0, pch = 16, col = "red")

# Add labels below the points
text(numbers, rep(-0.1, length(numbers)), labels = as.character(numbers), 
                                          cex = 0.8)

# Add label for the additional point
text(additional_point, -0.1, labels = "1/4", col = "red", cex = 0.8)

# Draw a horizontal line to represent the number line
abline(h = 0, col = "black")

# Add arrows at the ends of the number line
arrows(-10, 0, 10, 0, length = 0.1, code = 3)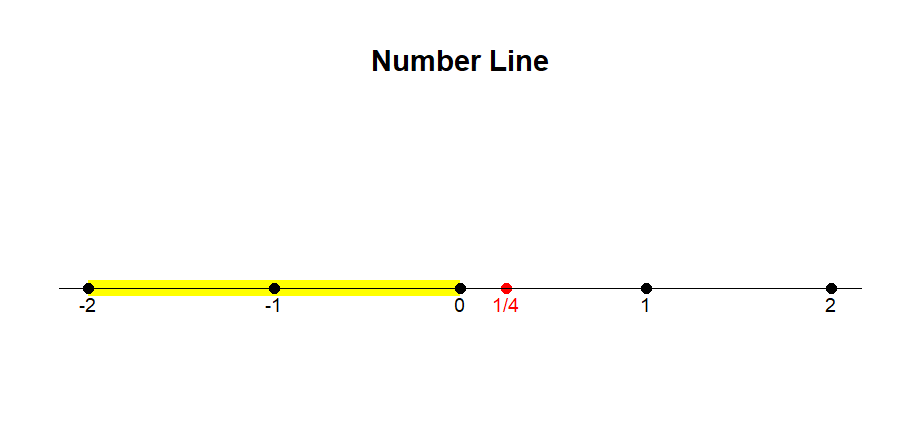

Analysing Julia Set

In the early \(20^{\text{th}}\) century mathematicians, Pierre Fatou and Gaston Julia set the stage for the discovery of the Mandelbrot set with their exploration of Dynamical Systems. To investigate these dynamical systems, mathematicians study intricate shapes which is known as Julia Sets. Julia Sets are produced by iterating a function of complex numbers.

Code 
import numpy as np 
import matplotlib.pyplot as plt 
import numpy as np

def julia_set(h_range, w_range, max_iterations):
    ''' A function to determine the values of the Julia set. Takes
    an array size specified by h_range and w_range, in pixels, along
    with the number of maximum iterations to try.  Returns an array with 
    the number of the last bounded iteration at each array value.
    '''
    # top left to bottom right
    y, x = np.ogrid[1.4: -1.4: h_range*1j, -1.4: 1.4: w_range*1j]
    z_array = x + y*1j
    a = -0.744 + 0.148j
    iterations_till_divergence = max_iterations + np.zeros(z_array.shape)
    
    for h in range(h_range):
        for w in range(w_range):
            z = z_array[h][w]
            for i in range(max_iterations):
                z = z**2 + a
                if z * np.conj(z) > 4:
                    iterations_till_divergence[h][w] = i
                    break

    return iterations_till_divergence

# Example usage
#result = julia_set(100, 100, 100)
#print(result)

plt.imshow(julia_set(1500, 1500, 1000), cmap='twilight_shifted')
plt.axis('off')
plt.show()

A complex number is defined as the sum of two components, a real part and an imaginary part. Each complex number can be visualized as a point of a 2D plane. The real part is a number found on the number line. The imaginary part is a multiple of the \(\sqrt{-1}\), which the mathematicians write as \(i\). Despite the name, imaginary numbers play a vital role in solving real-world problems. To construct Julia Set, start with a simple quadratic equation \(f(z) = z^2 +c\)

Code 
# Load the necessary library
library(ggplot2)

# Define a function to visualize complex numbers
visualize_complex_numbers <- function() {
  # Create a data frame of sample complex numbers
  complex_numbers <- data.frame(
    Real = c(-1, 0, 1, 1.5, -0.5, 2),
    Imaginary = c(1, -1, 0.5, -1.5, 1.5, -0.5)
  )
  
  # Create a ggplot
  ggplot(complex_numbers, aes(x = Real, y = Imaginary)) +
    geom_point(color = "blue", size = 4) +  # Plot points for complex numbers
    geom_hline(yintercept = 0, 
               linetype = "dashed") +  # Horizontal line at y=0 (real axis)
    geom_vline(xintercept = 0, 
               linetype = "dashed") +  # Vertical line at x=0 (imaginary axis)
    labs(
      title = "Visualization of Complex Numbers",
      x = "Real Part",
      y = "Imaginary Part"
    ) +
    theme_minimal() +
    theme(
      plot.title = element_text(hjust = 0.5)
    ) +
    annotate("text", x = 2, y = 0, label = "Real Axis", 
              vjust = -1, color = "red") +
    annotate("text", x = 0, y = 1.5, label = "Imaginary Axis", 
              hjust = -0.1, color = "red") +
    annotate("text", x = -1, y = 1, label = "-1 + 1i", 
              hjust = 1.2, vjust = -1.2, color = "darkgreen") +
    annotate("text", x = 0, y = -1, label = "0 - 1i", 
              hjust = 1.2, vjust = 1.2, color = "darkgreen") +
    annotate("text", x = 1, y = 0.5, label = "1 + 0.5i",
              hjust = -0.1, vjust = -1.2, color = "darkgreen") +
    annotate("text", x = 1.5, y = -1.5, label = "1.5 - 1.5i", 
              hjust = -0.1, vjust = 1.2, color = "darkgreen") +
    annotate("text", x = -0.5, y = 1.5, label = "-0.5 + 1.5i", 
              hjust = 1.2, vjust = -1.2, color = "darkgreen") +
    annotate("text", x = 2, y = -0.5, label = "2 - 0.5i", 
              hjust = -0.1, vjust = 1.2, color = "darkgreen")
}

# Call the function to visualize complex numbers
visualize_complex_numbers()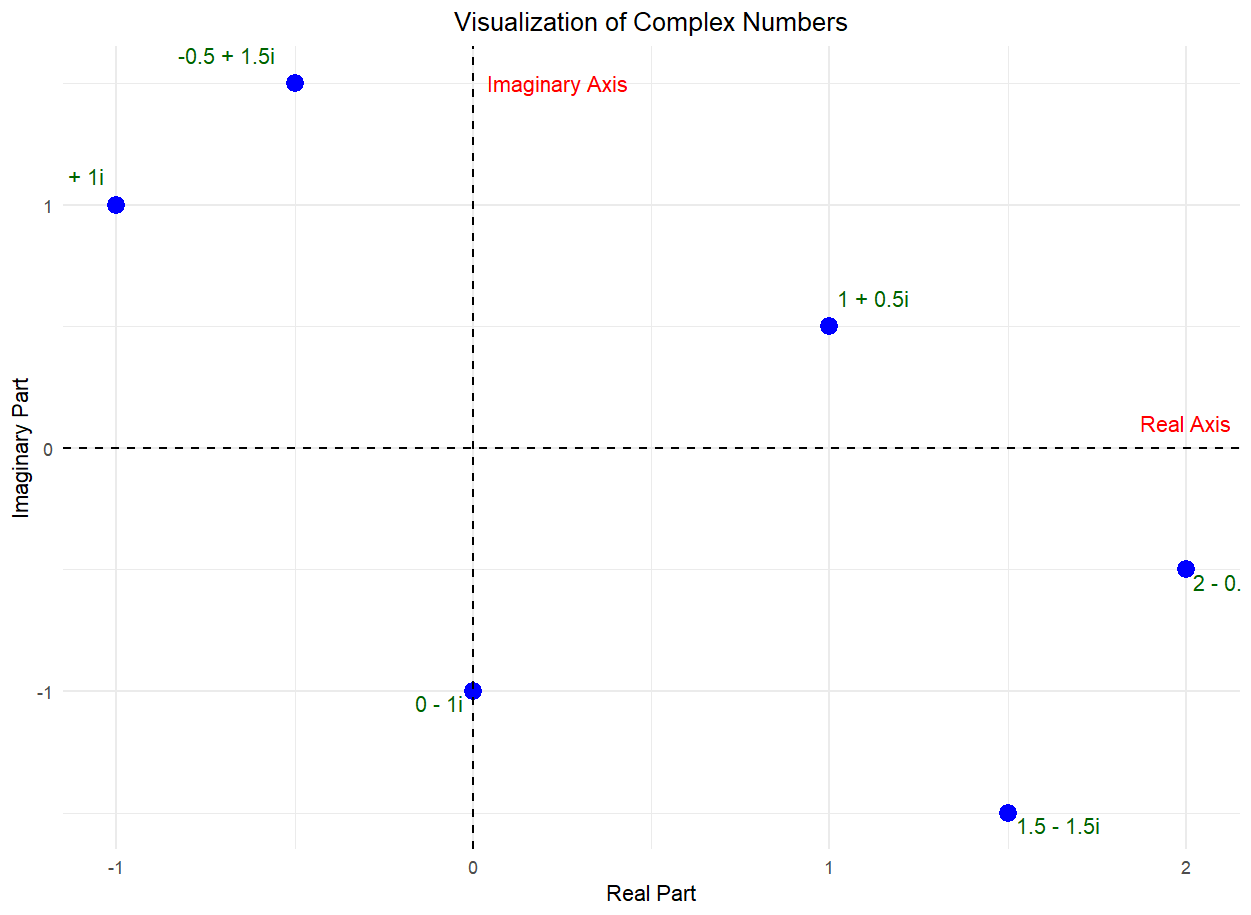

Choose a value for \(c=-1\) for example. Then consider what happens when you iterate this equation for every possible starting value.

You repeatedly apply the function to the sequence of numbers that you’re generating, and you ask whether or not that sequence is going off to infinity or whether it stay bounded.~ Laura Demarco (Mathematician, Havard)

For some initial values, your equation speeds off to infinity while iterating like these.These values are not in the Julia set. When you start iterating from other initial values, you might instead get a sequence of outputs that stay bounded.

Code 
# Load the necessary library
library(ggplot2)

# Define a function to visualize complex numbers
visualize_complex_numbers <- function() {
  # Create a data frame of sample complex numbers
  complex_numbers <- data.frame(
    Real = c(-1, 0, 1, 1.5, -0.5, 2, -2, 2.5, -1.5, 0.5),
    Imaginary = c(1, -1, 0.5, -1.5, 1.5, -0.5, 2, -2, 1.8, -2)
  )
  
  # Identify which points diverge to infinity
  diverges = c(FALSE, TRUE, FALSE, TRUE, FALSE, TRUE, TRUE, FALSE, TRUE, FALSE)
  
  # Add labels in the form of complex numbers
  complex_numbers$Labels <- paste0(complex_numbers$Real, 
                                   ifelse(complex_numbers$Imaginary >= 0, "+", ""), 
                                   complex_numbers$Imaginary, "i")
  
  # Create a ggplot
  ggplot(complex_numbers, aes(x = Real, y = Imaginary)) +
    geom_point(aes(color = diverges), size = 4) +  # Plot points for complex numbers with color indicating divergence
    geom_text(aes(label = Labels), vjust = -1.5, color = "black") +  # Add labels
    scale_color_manual(values = c("blue", "red"), labels = c("Bounded", "Diverges")) +  # Color and legend for points
    geom_hline(yintercept = 0, linetype = "dashed") +  # Horizontal line at y=0 (real axis)
    geom_vline(xintercept = 0, linetype = "dashed") +  # Vertical line at x=0 (imaginary axis)
    labs(
      title = "Visualization of Complex Numbers",
      x = "Real Part",
      y = "Imaginary Part",
      color = "Point Type"
    ) +
    theme_minimal() +
    theme(
      plot.title = element_text(hjust = 0.5)
    ) +
    annotate("text", x = 2, y = 0, label = "Real Axis", vjust = -1, color = "red") +
    annotate("text", x = 0, y = 1.5, label = "Imaginary Axis", hjust = -0.1, color = "red") +
    coord_fixed(ratio = 1, xlim = c(-3, 3), ylim = c(-3, 3)) # Adjust plot limits
}

# Call the function to visualize complex numbers
visualize_complex_numbers()


# Load the necessary library
library(ggplot2)

# Define a function to visualize complex numbers and their iterations
visualize_complex_numbers <- function() {
  # Create a data frame of sample complex numbers
  complex_numbers <- data.frame(
    Real = c(-1, 0, 1, 1.5, -0.5, 2, -2, 2.5, -1.5, 0.5),
    Imaginary = c(1, -1, 0.5, -1.5, 1.5, -0.5, 2, -2, 1.8, -2)
  )
  
  # Identify which points diverge to infinity
  diverges <- c(FALSE, TRUE, FALSE, TRUE, FALSE, TRUE, TRUE, FALSE, TRUE, FALSE)
  
  # Add labels in the form of complex numbers
  complex_numbers$Labels <- paste0(complex_numbers$Real, 
                                   ifelse(complex_numbers$Imaginary >= 0, "+", ""), 
                                   complex_numbers$Imaginary, "i")
  
  # Simulate iterations by adding more data points
  # Here we add a few iterations to demonstrate the idea
  iterations <- data.frame(
    Real = c(-1, -0.5, -0.5, 0, 0, 1, 1, 1.5, 1.5, -0.25, -0.25, 
             0.75, 0.75, 2, 2, -2, -2, -1.5, -1.5, 2.5, 2.5, 
             -1.5, -1.5, 0.5, 0.5, 0.75),
    Imaginary = c(1, 0.5, 0.5, -1, -1, 0, 0, 1.5, 1.5, -0.75, 
                  -0.75, 0.25, 0.25, -0.5, -0.5, 2, 2, 1.8, 1.8,
                  -2, -2, 0.9, 0.9, -2, -2, -1),
    Group = rep(1:13, each = 2) # Grouping for lines
  )
  
  # Create a ggplot
  ggplot(complex_numbers, aes(x = Real, y = Imaginary)) +
    geom_point(aes(color = diverges), size = 4) +  # Plot points for complex numbers with color indicating divergence
    geom_text(aes(label = Labels), vjust = -1.5, color = "black") +  # Add labels
    geom_path(data = iterations, aes(x = Real, y = Imaginary, group = Group), 
              color = "purple", linetype = "longdash") +  # Connect iteration points
    scale_color_manual(values = c("blue", "red"), 
                       labels = c("Bounded", "Diverges")) +  # Color and legend for points
    geom_hline(yintercept = 0, linetype = "dashed") +  # Horizontal line at y=0 (real axis)
    geom_vline(xintercept = 0, linetype = "dashed") +  # Vertical line at x=0 (imaginary axis)
    labs(
      title = "Visualization of Complex Numbers",
      x = "Real Part",
      y = "Imaginary Part",
      color = "Point Type"
    ) +
    theme_minimal() +
    theme(
      plot.title = element_text(hjust = 0.5)
    ) +
    annotate("text", x = 2, y = 0, label = "Real Axis", 
             vjust = -1, color = "red") +
    annotate("text", x = 0, y = 1.5, label = "Imaginary Axis", 
             hjust = -0.1, color = "red") +
    coord_fixed(ratio = 1, xlim = c(-3, 3), ylim = c(-3, 3)) # Adjust plot limits
}

# Call the function to visualize complex numbers
visualize_complex_numbers()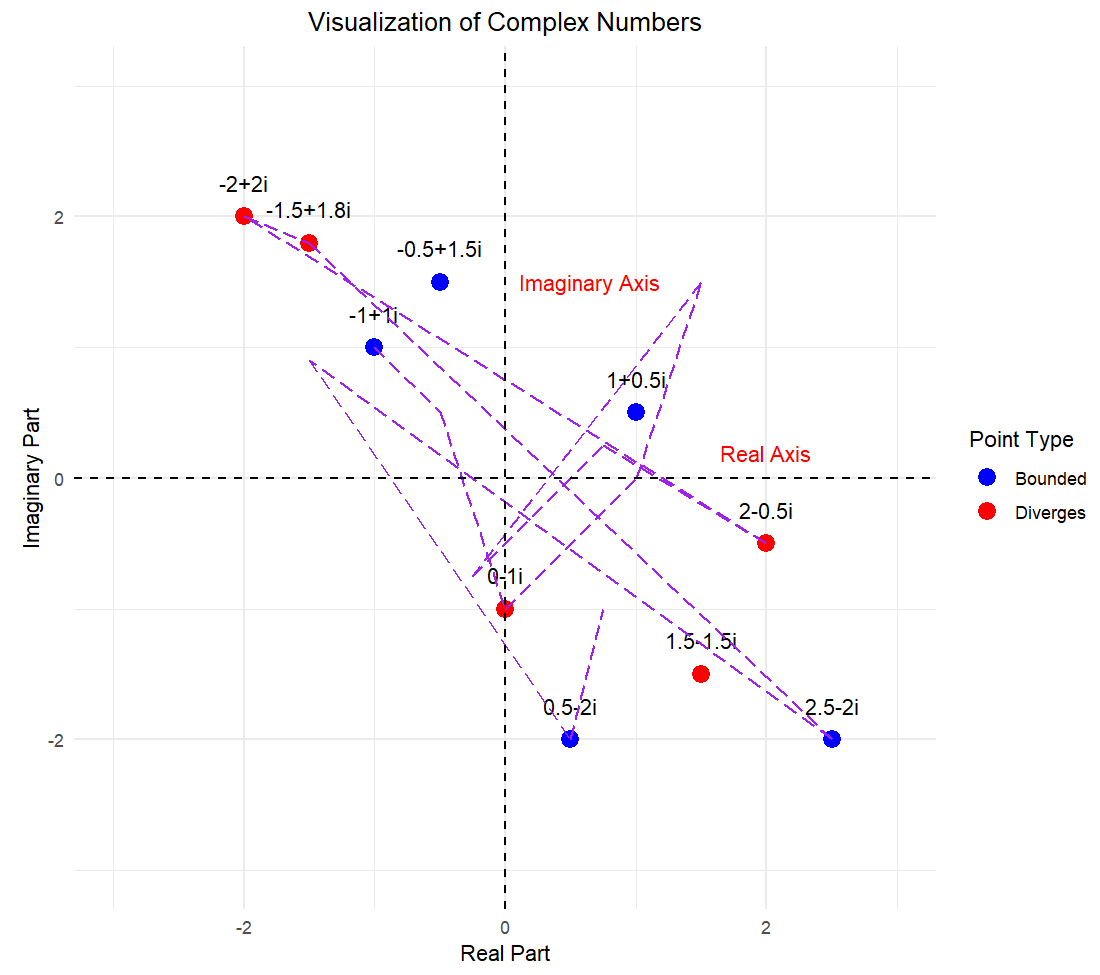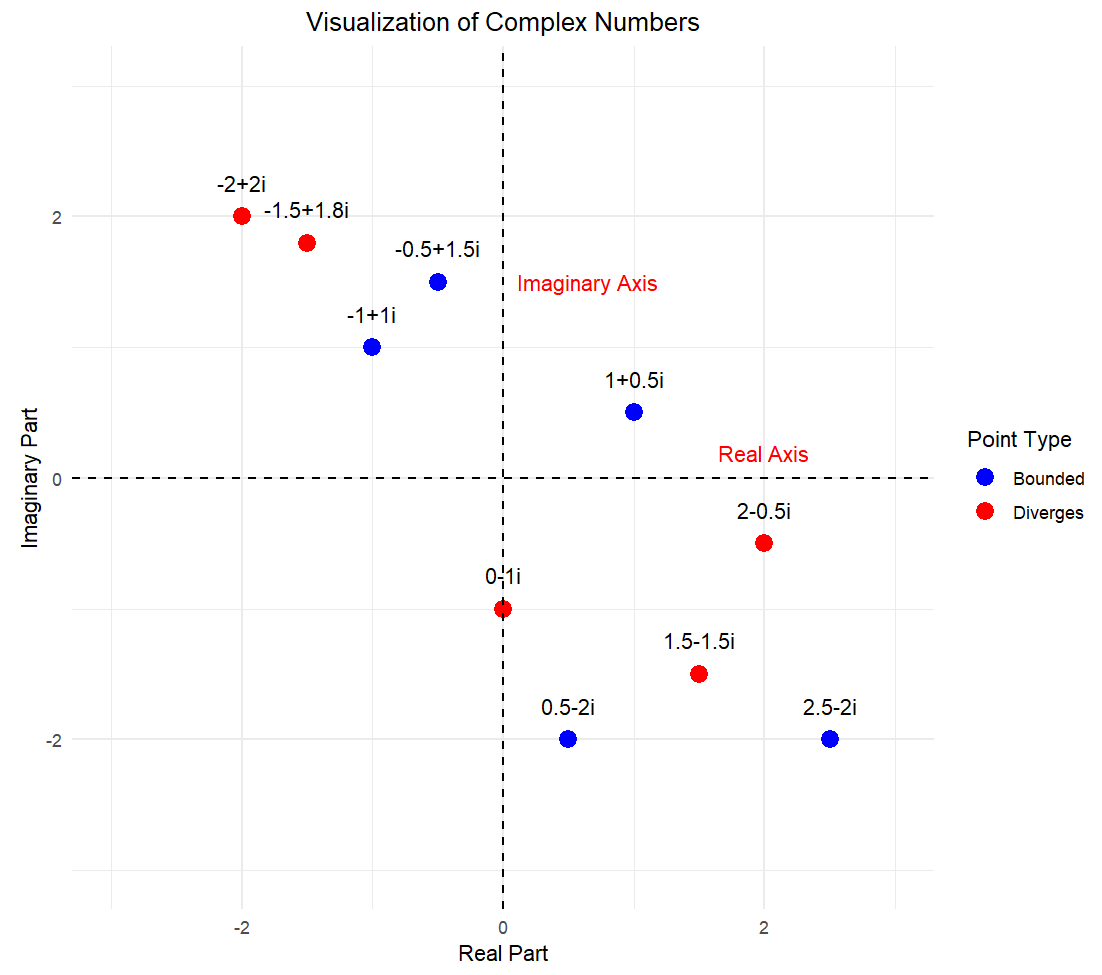

When something comes back to itself, we often call that recurrent behaviour, & that’s where the complexity arises.

Code 
# Load the necessary library
library(plotly)

# Define a function to visualize complex numbers and their iterations
visualize_complex_numbers_plotly <- function() {
  # Create a data frame of sample complex numbers
  complex_numbers <- data.frame(
    Real = c(-1, 0, 1, 1.5, -0.5, 2, -2, 2.5, -1.5, 0.5),
    Imaginary = c(1, -1, 0.5, -1.5, 1.5, -0.5, 2, -2, 1.8, -2),
    Diverges = c(FALSE, TRUE, FALSE, TRUE, FALSE, TRUE, TRUE, FALSE, TRUE, FALSE)
  )
  
  # Add labels in the form of complex numbers
  complex_numbers$Labels <- paste0(complex_numbers$Real, 
                                   ifelse(complex_numbers$Imaginary >= 0, "+", ""), 
                                   complex_numbers$Imaginary, "i")
  
  # Simulate iterations by adding more data points
  # Here we add a few iterations to demonstrate the idea
  iterations <- data.frame(
    Real = c(-1, -0.5, -0.5, 0, 0, 1, 1, 1.5, 1.5, -0.25, -0.25, 
             0.75, 0.75, 2, 2, -2, -2, -1.5, -1.5, 2.5, 2.5, 
             -1.5, -1.5, 0.5, 0.5, 0.75),
    Imaginary = c(1, 0.5, 0.5, -1, -1, 0, 0, 1.5, 1.5, -0.75, 
                  -0.75, 0.25, 0.25, -0.5, -0.5, 2, 2, 1.8, 1.8,
                  -2, -2, 0.9, 0.9, -2, -2, -1),
    Group = rep(1:13, each = 2) # Grouping for lines
  )
  
  # Create a plotly plot
  fig <- plot_ly() %>%
    add_markers(data = complex_numbers[complex_numbers$Diverges == FALSE,], 
                x = ~Real, y = ~Imaginary, 
                text = ~Labels, 
                textposition = 'top center',
                marker = list(size = 10, color = 'blue'),
                hoverinfo = 'text', 
                name = 'Bounded') %>%
    add_markers(data = complex_numbers[complex_numbers$Diverges == TRUE,], 
                x = ~Real, y = ~Imaginary, 
                text = ~Labels, 
                textposition = 'top center',
                marker = list(size = 10, color = 'red'),
                hoverinfo = 'text', 
                name = 'Diverges') %>%
    add_lines(data = iterations, 
              x = ~Real, y = ~Imaginary, 
              line = list(color = 'purple', dash = 'dash'),
              split = ~Group,
              showlegend = FALSE) %>%
    layout(title = "Visualization of Complex Numbers",
           xaxis = list(title = "Real Part", 
                        range = c(-3, 3), 
                        zeroline = TRUE, 
                        zerolinewidth = 1, 
                        zerolinecolor = 'black'),
           yaxis = list(title = "Imaginary Part", 
                        range = c(-3, 3), 
                        zeroline = TRUE, 
                        zerolinewidth = 1,
                        zerolinecolor = 'black'),
           shapes = list(
             list(type = "line", 
                  x0 = -3, 
                  x1 = 3,
                  y0 = 0, 
                  y1 = 0, 
                  line = list(dash = 'dash')),
             list(type = "line", 
                  x0 = 0, 
                  x1 = 0, 
                  y0 = -3, 
                  y1 = 3, 
                  line = list(dash = 'dash'))
           ),
           annotations = list(
             list(x = 2, 
                  y = 0, 
                  text = "Real Axis", 
                  showarrow = FALSE, 
                  font = list(color = "red")),
             list(x = 0, 
                  y = 1.5, 
                  text = "Imaginary Axis", 
                  showarrow = FALSE, 
                  font = list(color = "red"))
           ))
  
  # Display the plot
  fig
}

# Call the function to visualize complex numbers
visualize_complex_numbers_plotly()

The boundary between points that stay bounded and those that don’t is a Julia set. You can fill it in by including all the bounded values.

Code 
library(Julia)
imageN <- 2000
centre <- 0.0
L <- 4.0
C <- -0.8 + 0.156i
image_matrix <- JuliaImage(imageN, centre, L, C)
par(mar=c(0, 0, 0, 0))
image(image_matrix[550:1450, 200:1800], 
      col=hcl.colors(2000, palette="Roma"), 
      axes=FALSE, useRaster=TRUE)

Different quadratic equations generate a wide range of filled Julia sets. From basic Blobs to intricate twisting tendrils.

Code 
import argparse
import numpy as np
import cv2
from tqdm import tqdm


def generate_colors(n):
    palette = [(0, 0, 0)]
    img = np.zeros([1, 1, 3], dtype=np.uint8)
    for i in range(n):
        img[:] = ((i/n) * 255, 255 * 0.85, 255)
        rgb = cv2.cvtColor(img, cv2.COLOR_HSV2BGR)
        palette.append((rgb[0,0][0], rgb[0,0][1], rgb[0,0][2]))

    return palette


def interpolate(c1, c2, steps):
    delta1 = (c2[0] - c1[0]) / steps
    delta2 = (c2[1] - c1[1]) / steps
    res = []
    cc1 = c1[0]
    cc2 = c1[1]
    for i in range(steps):
        res.append((cc1, cc2))
        cc1 += delta1
        cc2 += delta2

    return res


def process_julia(max_iter, c, palette, width, height):
    w, h, zoom = width, height, 0.7
    move_x = 0.0
    move_y = 0.0
    img = np.zeros([h, w, 3], dtype=np.uint8)

    c_x = c[0]
    c_y = c[1]
    for x in range(w):
        for y in range(h):
            zx = 1.5 * (x - w / 2) / (0.5 * zoom * w) + move_x
            zy = 1.0 * (y - h / 2) / (0.5 * zoom * h) + move_y
            i = max_iter
            while zx * zx + zy * zy < 20 and i > 1:
                tmp = zx * zx - zy * zy + c_x
                zy, zx = 2.0 * zx * zy + c_y, tmp
                i -= 1

            index = (i * len(palette)) // max_iter
            img[y, x] = (palette[index][0], palette[index][1], palette[index][2])

    cv2.imshow('', img)
    cv2.waitKey(1)

    return img


if __name__ == '__main__':
    parser = argparse.ArgumentParser()
    parser.add_argument('-o', '--output', default='interpolate_Julia.mp4', type=str, help='resulting video')
    parser.add_argument('-i', '--iterations', default=100, type=int, help='number of iterations')
    args = parser.parse_args()
    print(args)

    width = 800
    height = 600

    interps = []
    num_iter = args.iterations

    interps.append(interpolate((-0.16, 1.0405), (-0.722, 0.246), num_iter))
    interps.append(interpolate((-0.722, 0.246), (-0.235125, 0.827215), num_iter))
    interps.append(interpolate((-0.235125, 0.827215),(-1.25066, 0.02012), num_iter))
    interps.append(interpolate((-1.25066, 0.02012), (-0.748, 0.1), num_iter))
    interps.append(interpolate((-0.748, 0.1), (-0.16, 1.0405), num_iter))
    pbar = tqdm(total=(num_iter * len(interps)))
    palette = generate_colors(2000)
    fourcc = cv2.VideoWriter_fourcc('F', 'M', 'P', '4')
    out_cutter_name = args.output
    fps = 24
    out = cv2.VideoWriter(out_cutter_name, fourcc, fps, (width, height))

    for interp in interps:
        for p in interp:
            r = process_julia(num_iter, p, palette, width, height)
            out.write(r)
            pbar.update(1)

    out.release()

Filled Julia sets can be divided into two categories. Sets are connected so that you can draw a line from one point to another without lifting your pen. Sets where points look like scattered pieces of dust are disconnected.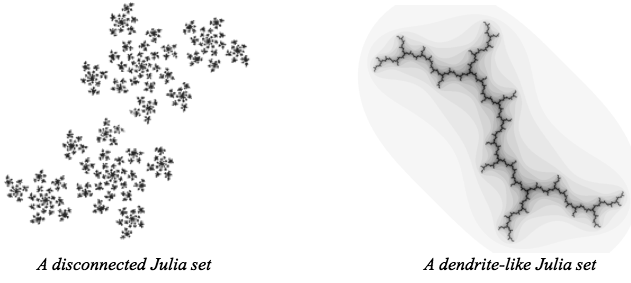

Elementary Complex Number

Let’s quickly explore the realm of complex numbers. The square root function identifies a number which, when multiplied by itself, yields the number under the radical. For instance, \(\sqrt{4}\)​ implies that since \(2\) times itself is \(4\), \(\sqrt{4}\) is \(2\).

Now, let’s consider the square root of a negative number. For example, what if we have \(\sqrt{-4}\)? Can you identify a number which, when multiplied by itself, equals \(-4\)?

The answer is you can’t, because there are no real numbers that satisfy this condition. This is because the square of any real number is always non-negative.

Similar questions arise with \(\sqrt{−1}\)​. What is the square root of \(-1\)?

The answer is that there are no real numbers that satisfy this condition. To address this, mathematicians introduced the concept of imaginary numbers. The square root of -1 is defined as \(i\), where \(i\) is the imaginary unit. Also, now we can answer about \(\sqrt{-4}\) i.e., \(\sqrt{-4} = 2i \times2i = (2.2) \times (i.i) = -4\).

Extension of \(f(z) = z^2 +c\) With Imaginary Number

So, Mandelbrot wanted to Inlcude imaginary numbers as well in his analysis of his function.

\[ f(z) = z^2 +c \]

Let’s try plug in \(i\) for \(c\) i.e., \(c =i\).

\[ f(0) = i \]

\[ f(i) = (i)^2 +1 = -1+i \]

\[ f(-1+i) = (-1+i)^2 + i = -i \]

Continuing the iterations by hand becomes increasingly complex, so we will pause here. It’s important to note that \(i\) is not included in the Mandelbrot set, as this function diverges to infinity. To visualize this, we can set up an imaginary number line. The bounds for this function are approximately \(-0.6i\) & \(0.6i\)

Code 
# Set up the plot area focusing on the imaginary part horizontally
plot(0, 0, type = "n", ylab = "", 
                       xlab = "Imaginary", 
                       xlim = c(-1, 1), 
                       ylim = c(-0.1, 0.1), 
                       yaxt = "n", main = "Imaginary Number Line")

# Draw the imaginary number line from -i to i
abline(h = 0, v = 0, col = "gray", lty = 2)  # Reference lines at the real axis
arrows(-1, 0, 1, 0, col = "black", length = 0.1)  # Arrow from -i to i

# Draw the shaded region from -0.6i to 0.6i
rect(-0.6, -0.02, 0.6, 0.02, col = "green", border = NA)

# Mark -i and i
points(-1, 0, pch = 16, col = "blue")
text(-1, -0.05, labels = "-i", col = "blue")
points(1, 0, pch = 16, col = "blue")
text(1, -0.05, labels = "i", col = "blue")

# Add labels for shaded region
points(-0.6, 0, pch = 16, col = "blue")
text(-0.6, -0.05, labels = "-0.6i", col = "blue")
points(0.6, 0, pch = 16, col = "blue")
text(0.6, -0.05, labels = "0.6i", col = "blue")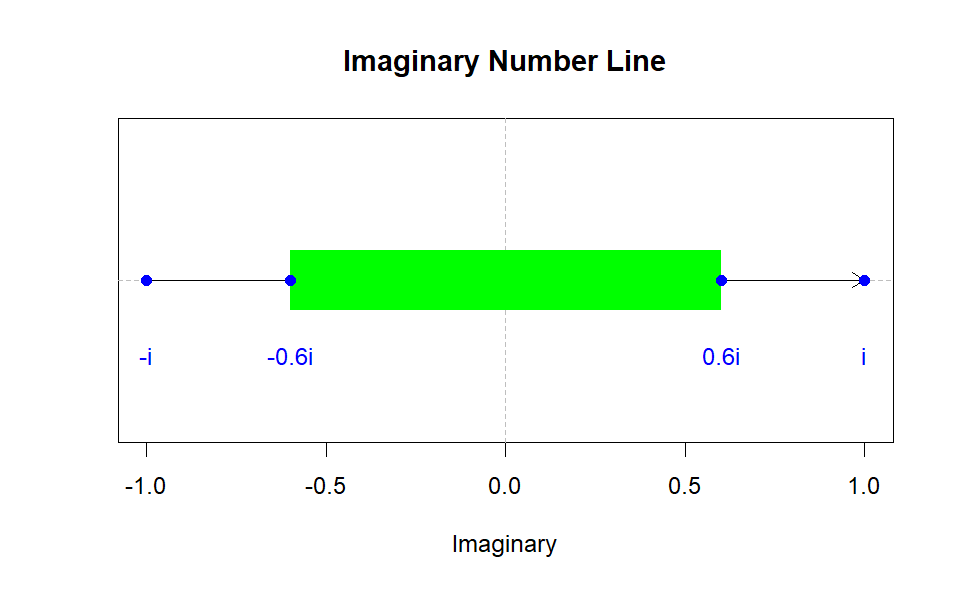

Many mathematicians might have stopped at this point, having defined the set for all real numbers and all imaginary numbers. However, there remains one more set of numbers to explore: complex numbers. Complex numbers consist of both a real and an imaginary component. This extension allows us to include complex numbers in our number system. A complex number can be expressed in the form \(a+bi\), where \(a\) and \(b\) are real numbers. This could be something as simple as \(1+i\) or as complex as \(6+9i\). If we let 𝑐c be any complex number, it can represent any combination of real and imaginary components.

Roughly \(-0.2 +1.12i\) is included in the Mandelbrot set

But where do we place this on the number line? We can’t simply put it above \(−0.2\) because we have \(0.2+1.12i\), where the real part is \(−0.2.\) If only there were some way to simultaneously represent both real and imaginary components. We need something like this:

Code 
# Set up the plot area
plot(0, 0, type = "n", xlab = "Real", 
           ylab = "Imaginary", 
           xlim = c(-2, 2), 
           ylim = c(-3, 1), main = "Number Line")

# Draw the imaginary number line from -3i to 1i
abline(h = 0, v = 0, col = "gray", lty = 2)  # Reference lines at real and imaginary axes
arrows(0, -3, 0, 1, col = "black", length = 0.1)  # Arrow from -3i to 1i

# Draw the real number line from -2 to 2
arrows(-2, 0, 2, 0, col = "black", length = 0.1)  # Arrow from -2 to 2

# Draw the shaded region from -2 to 0 on the real number line
rect(-2, -0.05, 0, 0.05, col = "yellow", border = NA)

# Draw the shaded region from -0.6i to 0.6i on the imaginary number line
rect(-0.05, -0.6, 0.05, 0.6, col = "green", border = NA)

# Mark -i and i on the imaginary axis
points(0, -1, pch = 16, col = "blue")
text(0.1, -1, labels = "-i", col = "blue")
points(0, 1, pch = 16, col = "blue")
text(0.1, 1, labels = "i", col = "blue")

# Add labels for shaded regions on the imaginary axis
points(0, -0.6, pch = 16, col = "blue")
text(0.1, -0.6, labels = "-0.6i", col = "blue")
points(0, 0.6, pch = 16, col = "blue")
text(0.1, 0.6, labels = "0.6i", col = "blue")

# Add labels for shaded regions on the real axis
points(-2, 0, pch = 16, col = "blue")
text(-2, 0.1, labels = "-2", col = "blue")
points(0, 0, pch = 16, col = "blue")
text(0, 0.1, labels = "0", col = "blue")

# Mark 1/4 on the real axis
points(0.25, 0, pch = 16, col = "red")
text(0.25, 0.1, labels = "1/4", col = "red")


# Load the necessary library
library(ggplot2)

# Create a data frame for the points and labels
points_data <- data.frame(
  x = c(0, 0, 0, 0, 0.25, -2, 0),
  y = c(-1, 1, -0.6, 0.6, 0, 0, 0),
  label = c("-i", "i", "-0.6i", "0.6i", "1/4", "-2", "0"),
  color = c("blue", "blue", "blue", "blue", "red", "blue", "blue")
)

# Create the base plot
p <- ggplot() +
  # Add the real number line
  geom_segment(aes(x = -2, y = 0, xend = 2, yend = 0), 
               arrow = arrow(length = unit(0.1, "inches")), 
               color = "black") +
  # Add the imaginary number line
  geom_segment(aes(x = 0, y = -3, xend = 0, yend = 1), 
               arrow = arrow(length = unit(0.1, "inches")), color = "black") +
  # Add the shaded region on the real number line
  annotate("rect", xmin = -2, xmax = 0, ymin = -0.05, 
            ymax = 0.05, alpha = 0.2, fill = "yellow") +
  # Add the shaded region on the imaginary number line
  annotate("rect", xmin = -0.05, xmax = 0.05, 
            ymin = -0.6, ymax = 0.6, alpha = 0.2, fill = "green") +
  # Add the points and labels
  geom_point(data = points_data, aes(x = x, y = y, color = color), size = 3) +
  geom_text(data = points_data, aes(x = x, y = y, label = label, color = color), hjust = 1.2, vjust = -0.5, size = 4) +
  # Set the axis labels and title
  labs(x = "Real", y = "Imaginary", title = "Number Line") +
  # Set the plot limits
  xlim(-2, 2) + ylim(-3, 1) +
  # Customize the theme
  theme_minimal() +
  theme(legend.position = "none")

# Display the plot
print(p)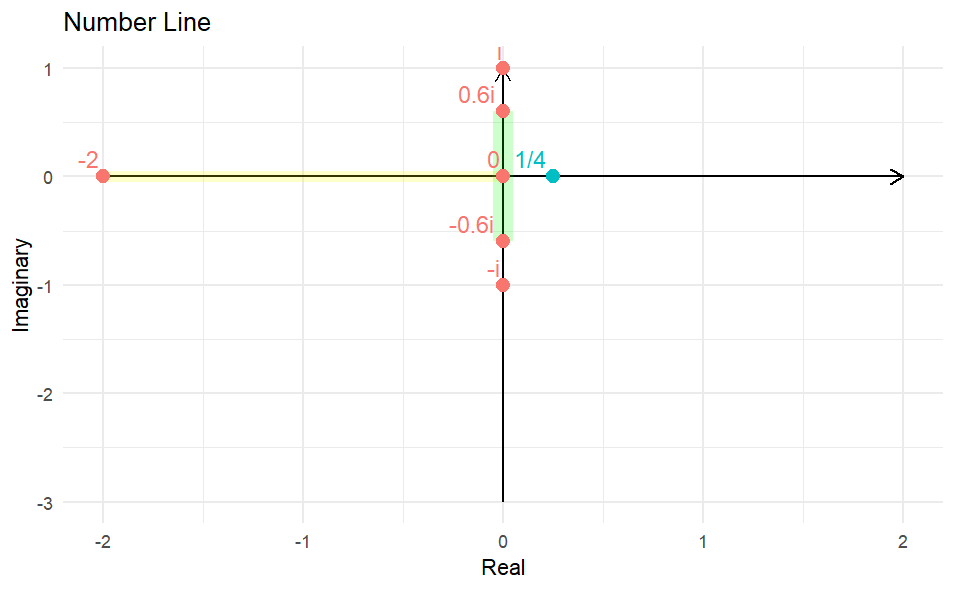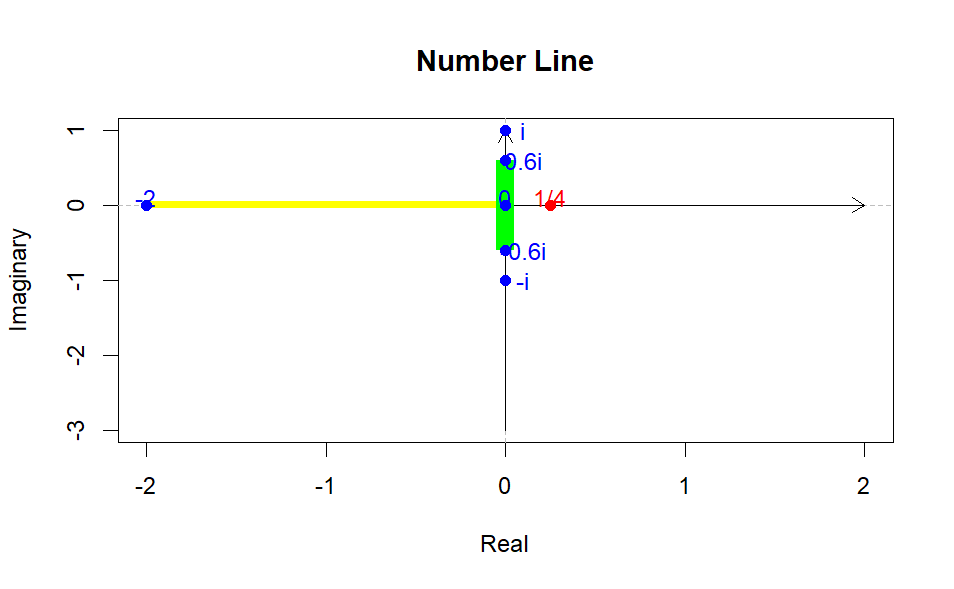

In this complex plane, we can plot complex numbers in the form \(a+bi\). The horizontal axis (real axis) represents the real part \(a\), and the vertical axis (imaginary axis) represents the imaginary part \(bi\). In this complex plane, each point \((a,b)\) corresponds to the complex number \(a+bi\). This way, both the real and imaginary parts of the number can be viewed together.

Code 
# Load the necessary library
library(ggplot2)

# Create a data frame for plotting the axes and labels
axes_data <- data.frame(
  x = c(3.5, 0),
  y = c(0, 3.5),
  label = c("Real Part", "Imaginary Part"),
  hjust = c(0.5, -0.1),
  vjust = c(-0.5, 0.5)
)

# Create the base plot
p <- ggplot() +
  # Add the real axis
  geom_segment(aes(x = -3, y = 0, xend = 3, yend = 0), 
               arrow = arrow(length = unit(0.2, "inches")), color = "black") +
  # Add the imaginary axis
  geom_segment(aes(x = 0, y = -3, xend = 0, yend = 3), 
               arrow = arrow(length = unit(0.2, "inches")), color = "black") +
  # Add axis labels
  geom_text(data = axes_data, aes(x = x, y = y, 
            label = label, hjust = hjust, vjust = vjust), size = 5) +
  # Set the plot limits
  xlim(-3.5, 3.5) + ylim(-3.5, 3.5) +
  # Customize the theme
  theme_minimal() +
  theme(axis.title = element_blank(),
        axis.text = element_blank(),
        axis.ticks = element_blank())

# Display the plot
print(p)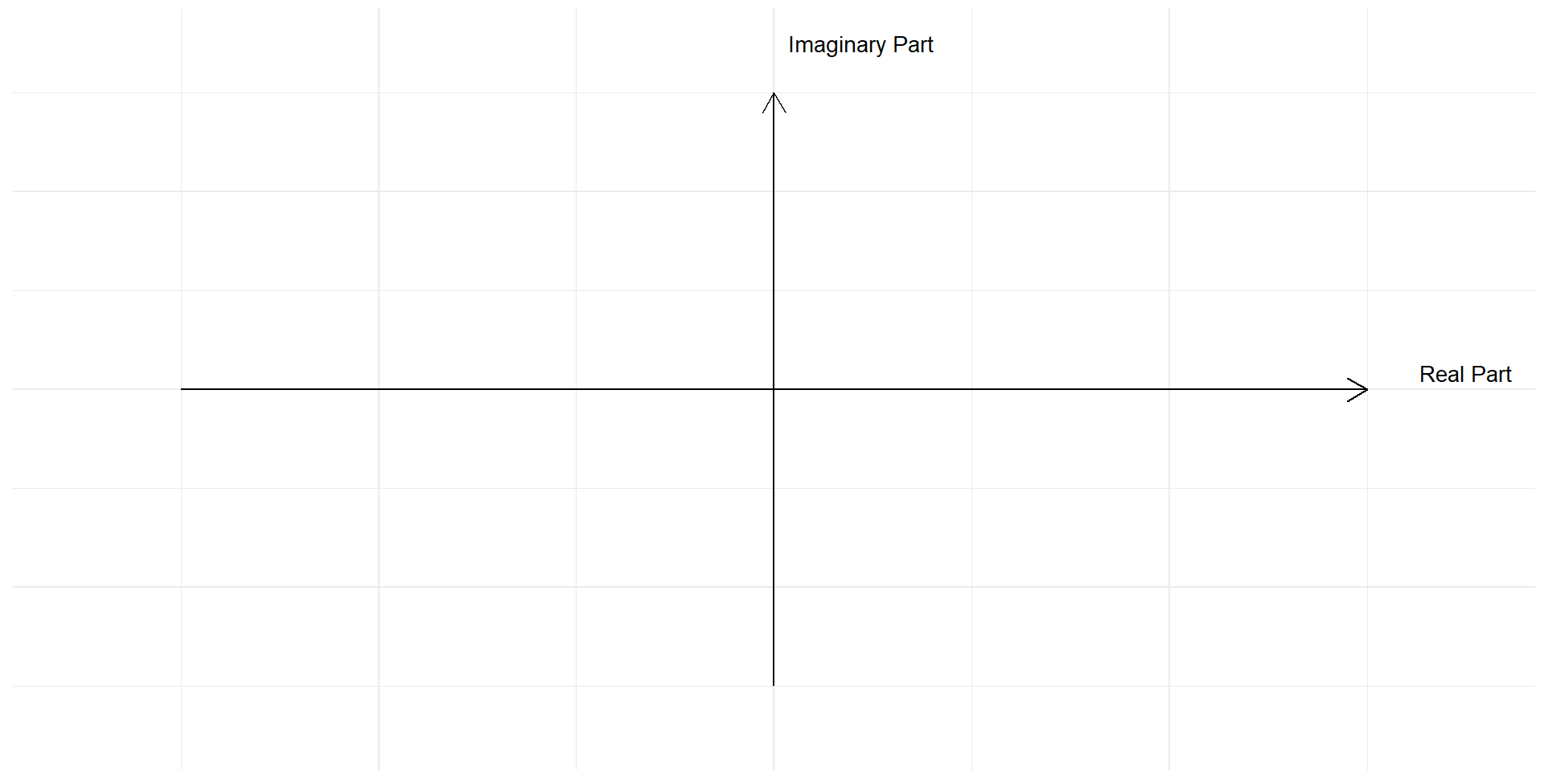

Given this framework, we are equipped to graph the Mandelbrot set. The Mandelbrot set consists of all complex numbers \(c\) for which the iterative sequence defined by the recurrence relation \(z_{n+1} = z_n^2+c\) (with \(z_0=0\) ) does not diverge to infinity. Mathematically, the Mandelbrot set is the set of all \(c\) in the complex plane such that the magnitude of \(z_n\)​ remains bounded as \(n\) approaches infinity. This intricate and beautiful set reveals the boundary between stability and chaos in complex dynamics, showcasing both self-similarity and fractal structure.

The Discovery of The Mandelbrot Set

The first rough plot of the Mandelbrot set appeared in a 1978 paper by the mathematicians Robert Brooks and J. Peter Matelski. Soon after Benoit Mandelbrot, a researcher at IBM, who had access to more computing power, also discovered the set. This led to further explorations. These early computer graphics were crude, but the patterns revealed the presence of something far more complex.

Even with fuzzy, poorly made pictures in the eighties, they were able to glean a lot of interesting insight into what was going on.

Mandelbrot went on to popularize his now-eponymous set to the world and became known as the father of fractals. Today mathematicians can use computers to explore the Mandelbrot set in far greater detail.

As soon as you have the images just opens up this whole world.

The Mandelbrot set is drawn in the complex plane. It is constructed by iterating the same quadratic equations used to produce Julia sets. But here things are flipped around. Instead of iterating all values of \(z\) for a fixed value of \(c\), we fix the starting value of the iteration at \(0\) and vary \(c\). Value of \(c\) where iteration of \(z^2+c\) stays bounded inside the Mandelbrot set. while those that go to infinity are not.

Here we can select points inside the Mandelbrot set to reveal their corresponding filled Julia sets. The Mandelbrot set acts like an atlas, cataloguing the different kinds of Julia sets. Values of \(c\) inside the Mandelbrot set are associated with connected Julia sets. While values outside the set correspond to disconnected dust.

The Mandelbrot set has many intriguing features, but the biggest mysteries lie in its complex fractal boundary. Zooming into different boundary regions reveals some astounding features. A valley of seahorses, parades of elephants and a miniature version of the set itself.

So, we can sort of keep finding nests, a sequence of smaller and smaller Mandelbrot sets. all one inside of the next.

Here at the boundary, mathematicians are probing for answers.

Code 
from PIL import Image
import colorsys
import math

px, py = -0.7746806106269039, -0.1374168856037867 #Tante Renate
R = 3 
max_iteration = 2500
w, h = 1024,1024
mfactor = 0.5

def Mandelbrot(x,y,max_iteration,minx,maxx,miny,maxy):
    zx = 0
    zy = 0
    RX1, RX2, RY1, RY2 = px-R/2, px+R/2,py-R/2,py+R/2
    cx = (x-minx)/(maxx-minx)*(RX2-RX1)+RX1
    cy = (y-miny)/(maxy-miny)*(RY2-RY1)+RY1
    i=0
    while zx**2 + zy**2 <= 4 and i < max_iteration:
        temp = zx**2 - zy**2
        zy = 2*zx*zy + cy
        zx = temp + cx
        i += 1
    return i

def gen_Mandelbrot_image(sequence):
  bitmap = Image.new("RGB", (w, h), "white")
  pix = bitmap.load()
  for x in range(w):
    for y in range(h):
      c=Mandelbrot(x,y,max_iteration,0,w-1,0,h-1)
      v = c**mfactor/max_iteration**mfactor
      hv = 0.67-v
      if hv<0: hv+=1
      r,g,b = colorsys.hsv_to_rgb(hv,1,1-(v-0.1)**2/0.9**2)
      r = min(255,round(r*255))
      g = min(255,round(g*255))
      b = min(255,round(b*255))
      pix[x,y] = int(r) + (int(g) << 8) + (int(b) << 16)
  bitmap.save("Mandelbrot_"+str(sequence)+".jpg")

R=3
f = 0.975
RZF = 1/1000000000000
k=1
while R>RZF:
  if k>100: break
  mfactor = 0.5 + (1/1000000000000)**0.1/R**0.1
  print(k,mfactor)
  gen_Mandelbrot_image(k)
  R *= f
  k+=1

As you look at it, it sort of seems like one blob, but if you really ask, is it all connected? or maybe if we zoom in far enough, there’s some separating piece.

Mandelbrot Locally Connected Conjecture(MLC)

This question is central to a 40-year-old problem called the Mandelbrot Locally Connected Conjecture(MLC). If the set is locally connected, that means that no matter what point you choose to examine or how far you zoom in, the are will always look like one nice connected section.

For example, if we closely examine a circle, we can see that it’s locally connected a every point, but take a fine-toothed comb and zoom in while the comb is one connected shape, at close range, it can look disconnected. If mathematicians can prove that MLC is true then a complete understanding of the Mandelbrot set would be within reach.

Normal Map Effect, Mercator Projection and Deep Zoom Images

Normalization, Distance Estimation and Boundary Detection

To visualize the Mandelbrot set with smooth colours, advanced colouring algorithms are employed. Techniques such as \(e^{-|z|}-\)smoothing, normalized iteration count, and exterior distance estimation are utilized. These methods are implemented using NumPy and complex matrices, as detailed in works by Javier Barrallo & Damien M. Jones (“Coloring Algorithms for Dynamical Systems in the Complex Plane”) and Arnaud Chéritat (“Boundary detection methods via distance estimators”).

Partial antialiasing is also applied to enhance boundary detection. The \(e^{-|z|}-\)smoothing technique ensures smooth transitions of colours based on the exponential decay of the distance from the Mandelbrot set boundary. Normalized iteration count allows for the differentiation of points based on how quickly they escape to infinity, and exterior distance estimation provides precise measurements of how far points are from the set’s boundary, thus aiding in accurate boundary depiction.

Code 
import numpy as np
import matplotlib.pyplot as plt

d, h = 800, 500  # pixel density (= image width) and image height
n, r = 200, 500  # number of iterations and escape radius (r > 2)

x = np.linspace(0, 2, num=d+1)
y = np.linspace(0, 2 * h / d, num=h+1)

A, B = np.meshgrid(x - 1, y - h / d)
C = 2.0 * (A + B * 1j) - 0.5

Z, dZ = np.zeros_like(C), np.zeros_like(C)
D, S, T = np.zeros(C.shape), np.zeros(C.shape), np.zeros(C.shape)

for k in range(n):
    M = abs(Z) < r
    S[M], T[M] = S[M] + np.exp(- abs(Z[M])), T[M] + 1
    Z[M], dZ[M] = Z[M] ** 2 + C[M], 2 * Z[M] * dZ[M] + 1

plt.imshow(S ** 0.1, cmap=plt.cm.twilight_shifted, origin="lower")
plt.savefig("Mandelbrot_set_1.png", dpi=200)

N = abs(Z) >= r  # normalized iteration count
T[N] = T[N] - np.log2(np.log(np.abs(Z[N])) / np.log(r))

plt.imshow(T ** 0.1, cmap=plt.cm.twilight_shifted, origin="lower")
plt.savefig("Mandelbrot_set_2.png", dpi=200)

N = abs(Z) > 2  # exterior distance estimation
D[N] = np.log(abs(Z[N])) * abs(Z[N]) / abs(dZ[N])

plt.imshow(D ** 0.1, cmap=plt.cm.twilight_shifted, origin="lower")
plt.savefig("Mandelbrot_set_3.png", dpi=200)

N, thickness = D > 0, 0.01  # boundary detection
D[N] = np.maximum(1 - D[N] / thickness, 0)

plt.imshow(D ** 2.0, cmap=plt.cm.binary, origin="lower")
plt.savefig("Mandelbrot_set_4.png", dpi=200)

These sophisticated methods not only enhance the visual appeal of the Mandelbrot set but also provide deeper insights into its complex structure. The use of NumPy and complex matrices allows for efficient computation and visualization, making it possible to explore the detailed and intricate patterns of this fascinating fractal.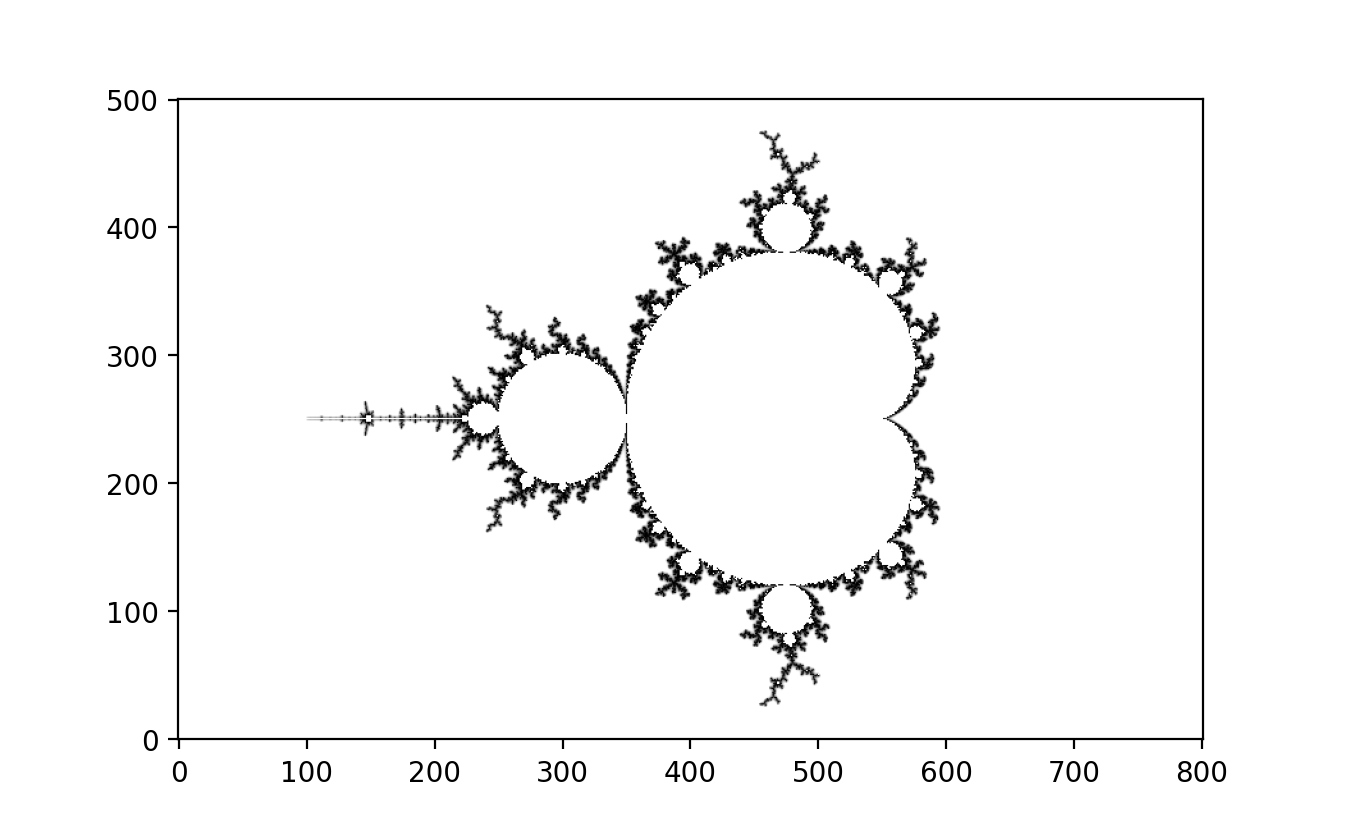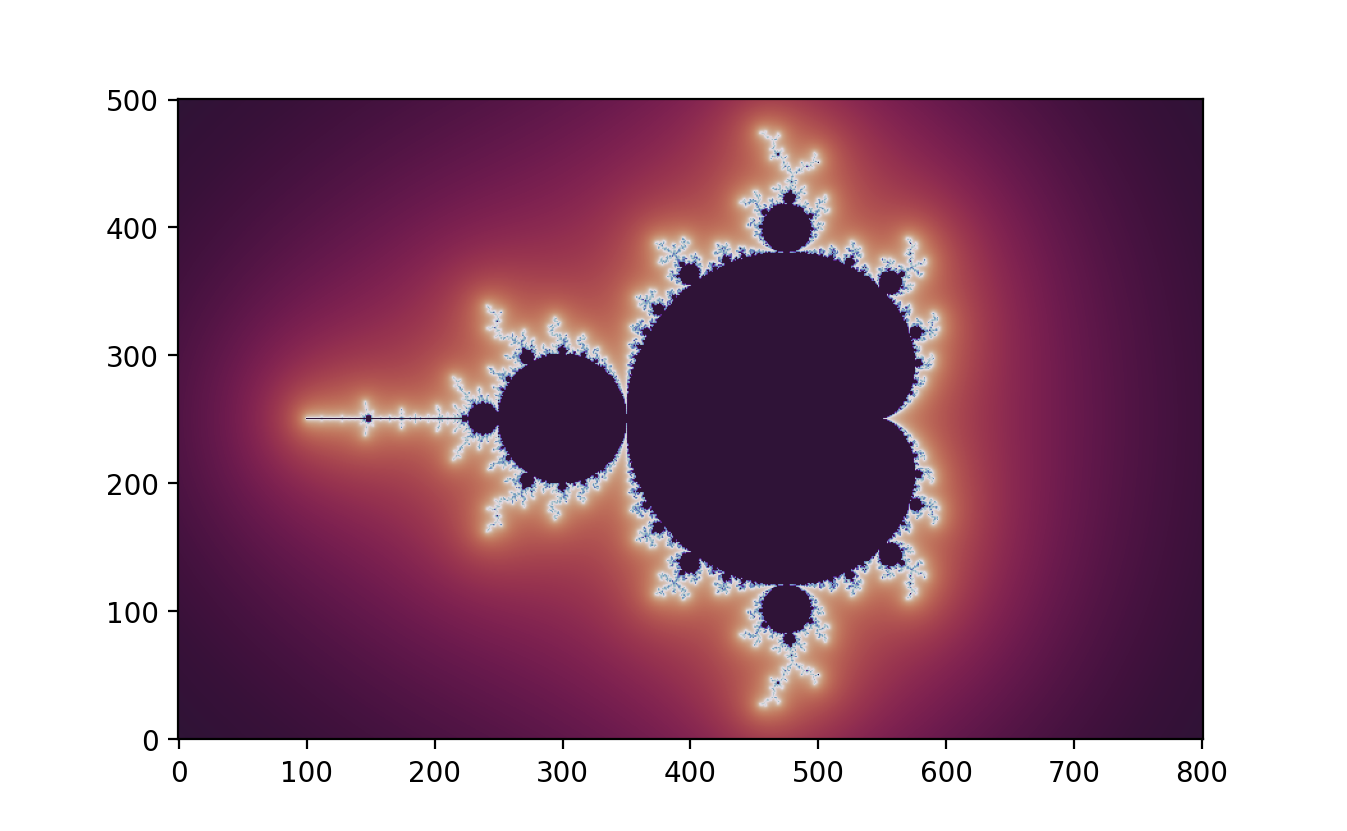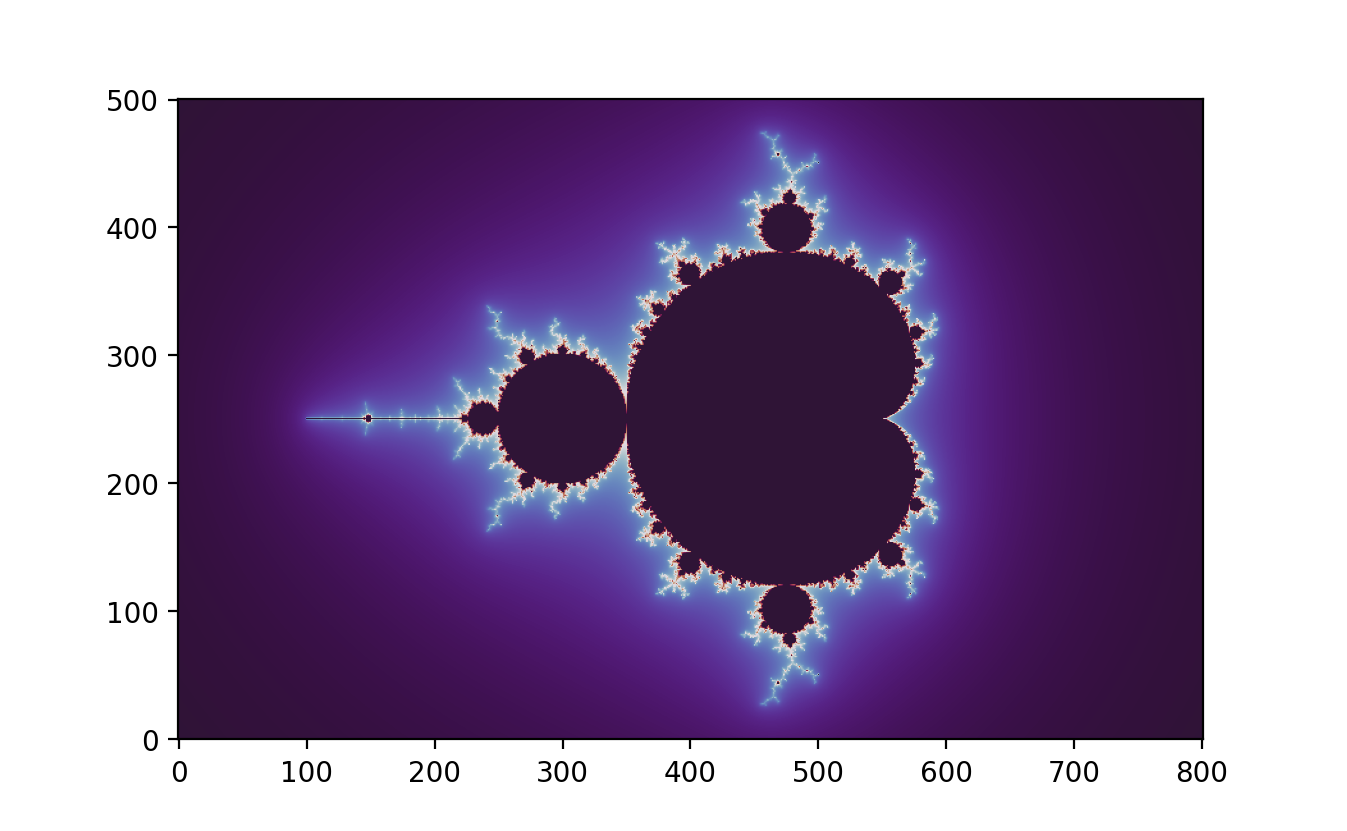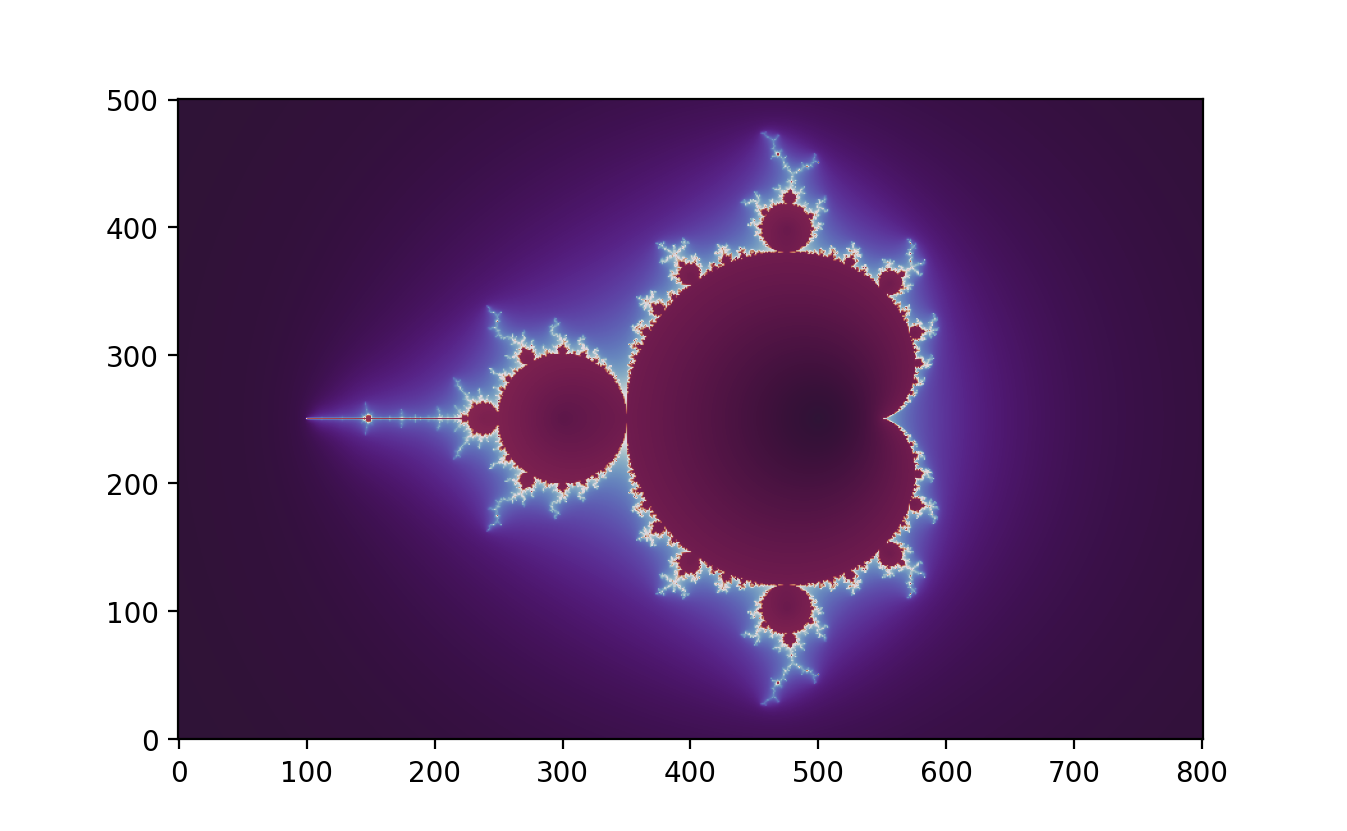

Normal Map Effect and Stripe Average Coloring

The Mandelbrot set is often visualized using advanced techniques such as Normal Maps and Stripe Average Coloring, enhancing its visual representation. Developed by Jussi Härkönen and building on Arnaud Chéritat’s work, these methods significantly enrich the fractal’s appearance.

The Normal Map Effect simulates lighting by perturbing surface normals, giving the fractal a three-dimensional look. Stripe Average Coloring adds patterns to highlight complex boundaries. Due to the rapid growth of the second derivative, Stripe Average Coloring is most effective for iterations \(n \leq 400.\)

To achieve stripe patterns similar to Arnaud Chéritat’s:

  • Increase stripe density.

  • Use the cosine function (\(\cos\)) instead of sine function (\(\sin\)).

  • Apply a binary colormap for high contrast.

Implementation Techniques

Using NumPy and complex matrices, these methods leverage normalized iteration count and exterior distance estimation for smooth transitions and precise boundary detection. Techniques like \(e^{-|z|}-\)smoothing ensure smooth color gradients based on exponential decay from the Mandelbrot set boundary.

Code 
#Normal Map Effect and Stripe Average Coloring

import numpy as np
import matplotlib.pyplot as plt

d, h = 800, 500  # pixel density (= image width) and image height
n, r = 200, 500  # number of iterations and escape radius (r > 2)

direction, height = 45.0, 1.5  # direction and height of the light
density, intensity = 4.0, 0.5  # density and intensity of the stripes

x = np.linspace(0, 2, num=d+1)
y = np.linspace(0, 2 * h / d, num=h+1)

A, B = np.meshgrid(x - 1, y - h / d)
C = (2.0 + 1.0j) * (A + B * 1j) - 0.5

Z, dZ, ddZ = np.zeros_like(C), np.zeros_like(C), np.zeros_like(C)
D, S, T = np.zeros(C.shape), np.zeros(C.shape), np.zeros(C.shape)

for k in range(n):
    M = abs(Z) < r
    S[M], T[M] = S[M] + np.sin(density * np.angle(Z[M])), T[M] + 1
    Z[M], dZ[M], ddZ[M] = Z[M] ** 2 + C[M], 2 * Z[M] * dZ[M] + 1, 2 * (dZ[M] ** 2 + Z[M] * ddZ[M])

N = abs(Z) >= r  # basic normal map effect and stripe average coloring (potential function)
P, Q = S[N] / T[N], (S[N] + np.sin(density * np.angle(Z[N]))) / (T[N] + 1)
U, V = Z[N] / dZ[N], 1 + (np.log2(np.log(np.abs(Z[N])) / np.log(r)) * (P - Q) + Q) * intensity
U, v = U / abs(U), np.exp(direction / 180 * np.pi * 1j)  # unit normal vectors and light vector
D[N] = np.maximum((U.real * v.real + U.imag * v.imag + V * height) / (1 + height), 0)

plt.imshow(D ** 1.0, cmap=plt.cm.bone, origin="lower")
plt.savefig("Mandelbrot_normal_map_1.png", dpi=200)

N = abs(Z) > 2  # advanced normal map effect using higher derivatives (distance estimation)
U = Z[N] * dZ[N] * ((1 + np.log(abs(Z[N]))) * np.conj(dZ[N] ** 2) - np.log(abs(Z[N])) * np.conj(Z[N] * ddZ[N]))
U, v = U / abs(U), np.exp(direction / 180 * np.pi * 1j)  # unit normal vectors and light vector
D[N] = np.maximum((U.real * v.real + U.imag * v.imag + height) / (1 + height), 0)

plt.imshow(D ** 1.0, cmap=plt.cm.afmhot, origin="lower")
plt.savefig("Mandelbrot_normal_map_2.png", dpi=200)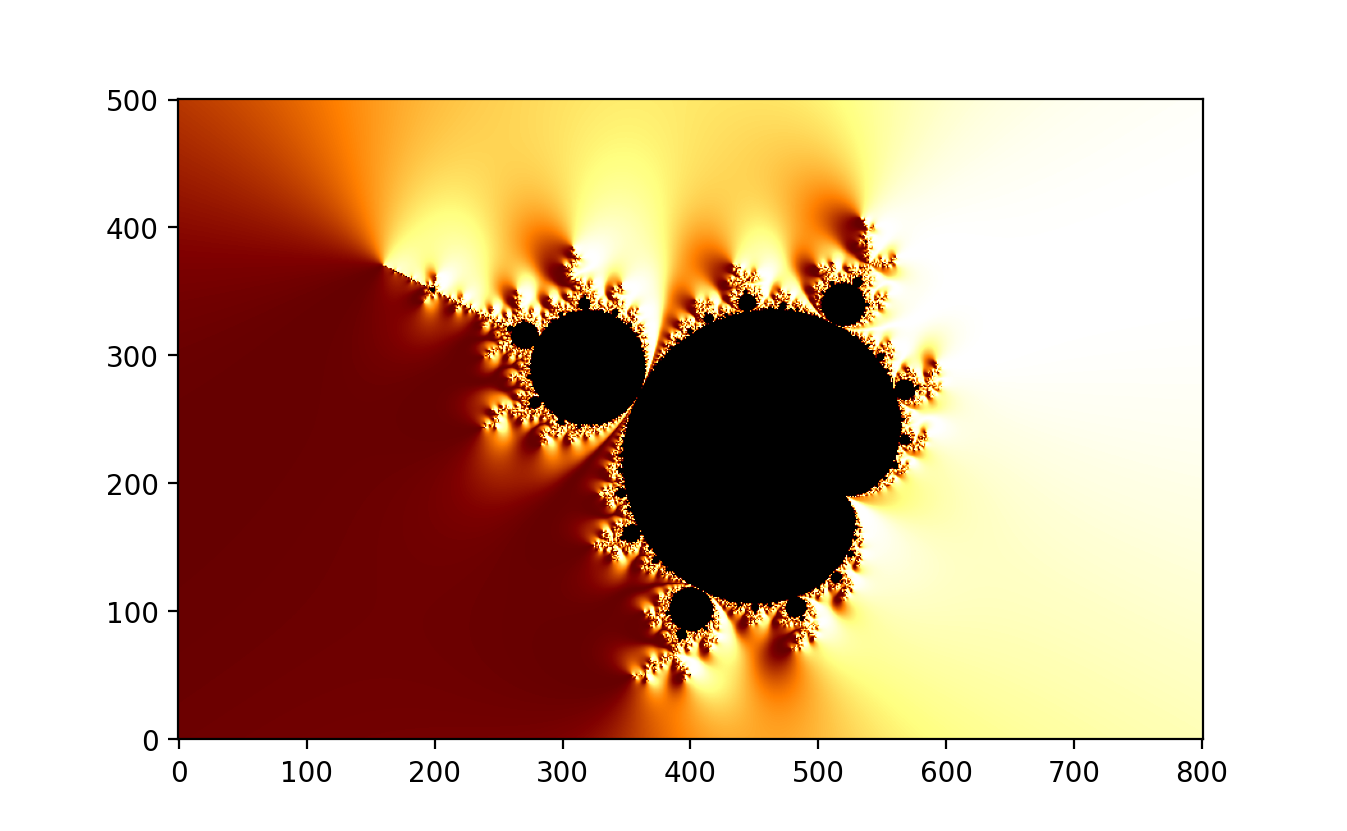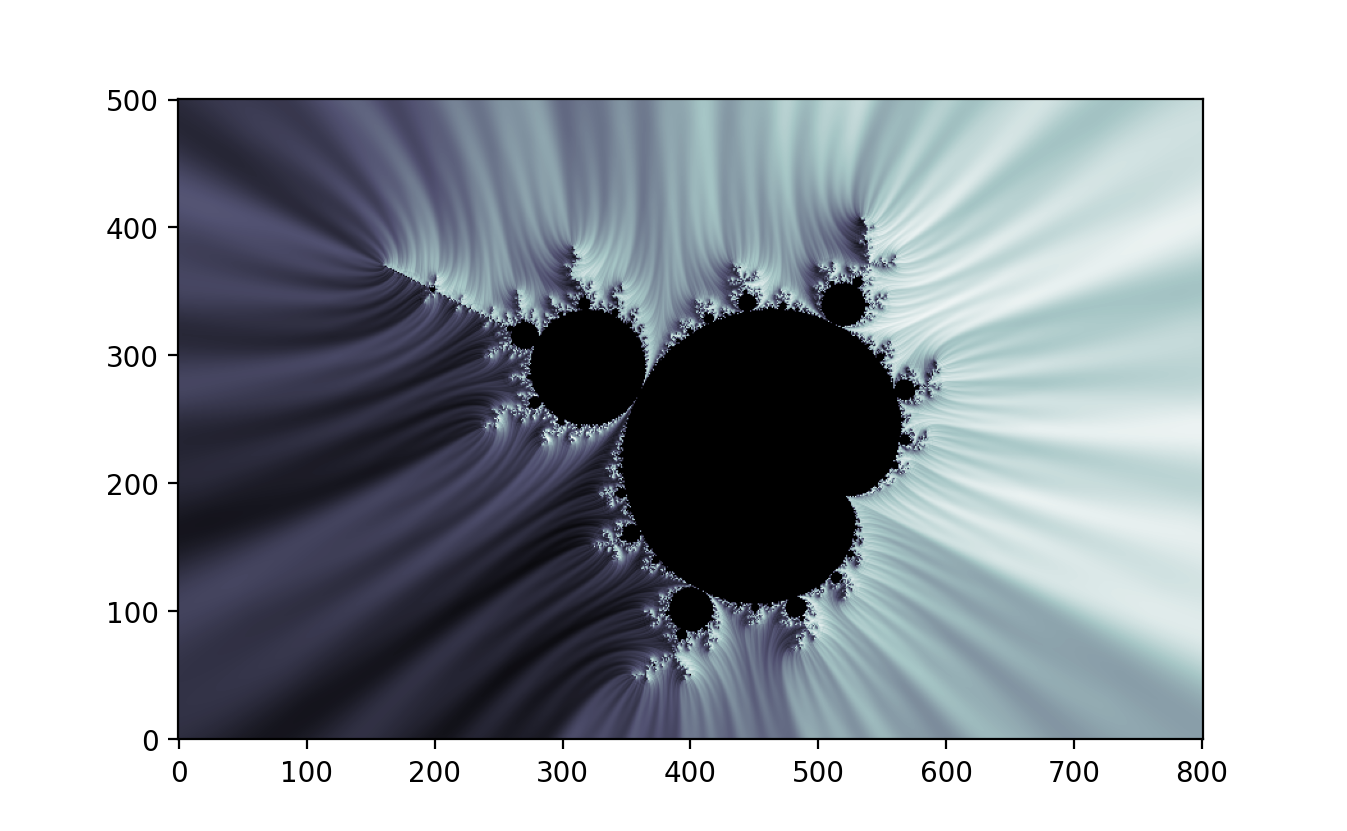

Practical Applications

Platforms like Shadertoy showcase practical implementations of these methods, such as in sections “Mixing it all” and “Julia Stripes,” allowing interactive visualizations of the Mandelbrot set. Normal Map Effect and Stripe Average Coloring enhance the visualization of the Mandelbrot set, revealing its intricate beauty and complexity. These advanced techniques provide deeper insights into fractal geometry and complex dynamics.

Mercator Mandelbrot Maps and Zoom Images

A small modification in the code allows for the creation of Mercator maps of the Mandelbrot set, as demonstrated by David Madore and Anders Sandberg. These maps offer a unique perspective on the fractal’s structure, enabling detailed exploration and magnification. The maximum magnification achievable with this method is approximately:

\[ e^{2\pi. \frac{h}{d}} = e^{2\pi.5.5} \approx 535.5^{5.5} \approx 10^{15} \]

This represents the maximum magnification for \(64-\)bit arithmetic. Anders Sandberg, however, employs a different scaling approach. He uses:

\[ 10^{3.\frac{h}{d}} = 1000^{\frac{h}{d}} \]

This scaling method results in images that appear slightly compressed compared to those generated using \(e^{2\pi. \frac{h}{d}} \approx 535.5^{\frac{h}{d}}\). Despite this difference, the compression is minimal because:

\[ 1000^{5.0} \approx 535.5^{5.5} \]

With identical pixel density and maximum magnification, the height difference between the maps is only about \(10\)%.

Zooming into the Mandelbrot Set & Julia Set

Zooming into the Mandelbrot set and Julia set reveals the intricate and infinitely complex nature of these famous fractals. The Mandelbrot set, plotted in the complex plane, is defined by iterating the function \(f(z) = z^2+c\) and determining whether the sequence remains bounded. Each zoom into the Mandelbrot set unveils self-similar structures and increasingly detailed patterns, showcasing its fractal nature.

Similarly, Julia sets are generated using a similar iterative process, but for each fixed complex parameter \(c\). Each point in the complex plane is tested to see if the sequence remains bounded. Julia sets exhibit a variety of shapes, depending on the value of \(c\), ranging from connected, cloud-like formations to disconnected, dust-like patterns.

Advanced visualization techniques, such as deep zoom images and projections, enhance the exploration of these sets. These tools allow mathematicians and enthusiasts to delve into the fine details, revealing the endless complexity and beauty hidden within the Mandelbrot and Julia sets. This exploration not only serves as a source of aesthetic pleasure but also provides insights into the mathematical properties and dynamics of complex systems.

Zooming \(10^{13}\) Times into Mandelbrot Set Animation

Code 
from PIL import Image
import colorsys
import math

px, py = -0.7746806106269039, -0.1374168856037867 #Tante Renate
R = 3 
max_iteration = 2500
w, h = 1024,1024
mfactor = 0.5

def Mandelbrot(x,y,max_iteration,minx,maxx,miny,maxy):
    zx = 0
    zy = 0
    RX1, RX2, RY1, RY2 = px-R/2, px+R/2,py-R/2,py+R/2
    cx = (x-minx)/(maxx-minx)*(RX2-RX1)+RX1
    cy = (y-miny)/(maxy-miny)*(RY2-RY1)+RY1
    i=0
    while zx**2 + zy**2 <= 4 and i < max_iteration:
        temp = zx**2 - zy**2
        zy = 2*zx*zy + cy
        zx = temp + cx
        i += 1
    return i

def gen_Mandelbrot_image(sequence):
  bitmap = Image.new("RGB", (w, h), "white")
  pix = bitmap.load()
  for x in range(w):
    for y in range(h):
      c=Mandelbrot(x,y,max_iteration,0,w-1,0,h-1)
      v = c**mfactor/max_iteration**mfactor
      hv = 0.67-v
      if hv<0: hv+=1
      r,g,b = colorsys.hsv_to_rgb(hv,1,1-(v-0.1)**2/0.9**2)
      r = min(255,round(r*255))
      g = min(255,round(g*255))
      b = min(255,round(b*255))
      pix[x,y] = int(r) + (int(g) << 8) + (int(b) << 16)
  bitmap.save("Mandelbrot_"+str(sequence)+".jpg")

R=3
f = 0.975
RZF = 1/1000000000000
k=1
while R>RZF:
  if k>100: break
  mfactor = 0.5 + (1/1000000000000)**0.1/R**0.1
  print(k,mfactor)
  gen_Mandelbrot_image(k)
  R *= f
  k+=1

Zooming \(10^{13}\) Times into Julia Set Animation

Code 
from PIL import Image
import colorsys

cx = -0.7269
cy = 0.1889
R = (1+(1+4*(cx**2+cy**2)**0.5)**0.5)/2+0.001
max_iteration = 512
print(R)

w, h, zoom = 1500,1500,1

def julia(cx,cy,RZ,px,py,R,max_iteration,x,y,minx,maxx,miny,maxy):
    zx = (x-minx)/(maxx-minx)*2*RZ-RZ+px
    zy = (y-miny)/(maxy-miny)*2*RZ-RZ+py
    i=0
    while zx**2 + zy**2 < R**2 and i < max_iteration:
        temp = zx**2 - zy**2
        zy = 2*zx*zy + cy
        zx = temp + cx
        i += 1
    return i

def gen_julia_image(sequence,cx,cy,RZ):
  bitmap = Image.new("RGB", (w, h), "white")
  pix = bitmap.load()
  for x in range(w):
    for y in range(h):
        # smllaer: right,down
      c=julia(cx,cy,RZ,0.0958598997051,1.1501990019993,R,max_iteration,x,y,0,w-1,0,h-1)
      v = c/max_iteration
      hv = 0.67-v*0.67
      r,g,b = colorsys.hsv_to_rgb(hv,1,v/2+0.45)
      r = min(255,round(r*255))
      g = min(255,round(g*255))
      b = min(255,round(b*255))
      pix[x,y] = int(r) + (int(g) << 8) + (int(b) << 16)
  bitmap.save("julia_"+str(sequence)+".jpg")
#  bitmap.show()

f = 0.95
RZF = 1/1000000000000
RZ = 1
k=1
while RZ>RZF:
  print(k,RZ)
  gen_julia_image(k,0.355,0.355,RZ)
  RZ *= f
  k+=1

Mathematical Insight

The Mercator projection, traditionally used for geographical maps, can be adapted to map the complex plane of the Mandelbrot set. The projection formula \(e^{2\pi \cdot \frac{h}{d}}\) reflects the exponential growth in magnification as one zooms into the fractal. This exponential scaling is essential for revealing the intricate details of the Mandelbrot set, which are not apparent at lower magnifications. In contrast, Sandberg’s use of the logarithmic scaling \(10^{3 \cdot \frac{h}{d}}\) provides an alternative method for visualizing the fractal. This logarithmic approach, although slightly different, still captures the essential features of the Mandelbrot set, highlighting its complex boundaries and internal structures.

The use of Mercator maps and innovative plotting techniques opens new avenues for exploring the Mandelbrot set. These methods reveal the fractal’s rich and intricate structure, offering insights into its mathematical beauty. By leveraging different scaling approaches and visualization techniques, researchers can gain a deeper understanding of the complex dynamics underlying the Mandelbrot set. For further exploration, one can refer to works such as David Madore’s “Mandelbrot set images and videos” and Anders Sandberg’s “Mercator Mandelbrot Maps,” which provide practical implementations and visualizations of these concepts.

Practical Considerations

Creating high-quality zoom images of the Mandelbrot set requires careful consideration of computational limits. The maximum magnification achievable with 64-bit arithmetic imposes a constraint on the depth of zoom. This constraint necessitates efficient algorithms and data structures to handle the large numbers and extensive computations involved in rendering detailed fractal images.

Code 
# Mercator Mandelbrot Maps and Zoom Images

import numpy as np
import matplotlib.pyplot as plt

d, h = 200, 1200  # pixel density (= image width) and image height
n, r = 8000, 10000  # number of iterations and escape radius (r > 2)

a = -.743643887037158704752191506114774  # https://mathr.co.uk/web/m-location-analysis.html
b = 0.131825904205311970493132056385139  # try: a, b, n = -1.748764520194788535, 3e-13, 800

x = np.linspace(0, 2, num=d+1)
y = np.linspace(0, 2 * h / d, num=h+1)

A, B = np.meshgrid(x * np.pi, y * np.pi)
C = 8.0 * np.exp((A + B * 1j) * 1j) + (a + b * 1j)

Z, dZ = np.zeros_like(C), np.zeros_like(C)
D = np.zeros(C.shape)

for k in range(n):
    M = Z.real ** 2 + Z.imag ** 2 < r ** 2
    Z[M], dZ[M] = Z[M] ** 2 + C[M], 2 * Z[M] * dZ[M] + 1

N = abs(Z) > 2  # exterior distance estimation
D[N] = np.log(abs(Z[N])) * abs(Z[N]) / abs(dZ[N])

plt.imshow(D.T ** 0.05, cmap=plt.cm.nipy_spectral, origin="lower")
plt.savefig("Mercator_Mandelbrot_map.png", dpi=200)

X, Y = C.real, C.imag  # zoom images (adjust circle size 100 and zoom level 20 as needed)
R, c, z = 100 * (2 / d) * np.pi * np.exp(- B), min(d, h) + 1, max(0, h - d) // 20

fig, ax = plt.subplots(2, 2, figsize=(12, 12))
ax[0,0].scatter(X[1*z:1*z+c,0:d], Y[1*z:1*z+c,0:d], s=R[0:c,0:d]**2, c=D[1*z:1*z+c,0:d]**.5, cmap=plt.cm.nipy_spectral)
ax[0,1].scatter(X[2*z:2*z+c,0:d], Y[2*z:2*z+c,0:d], s=R[0:c,0:d]**2, c=D[2*z:2*z+c,0:d]**.4, cmap=plt.cm.nipy_spectral)
ax[1,0].scatter(X[3*z:3*z+c,0:d], Y[3*z:3*z+c,0:d], s=R[0:c,0:d]**2, c=D[3*z:3*z+c,0:d]**.3, cmap=plt.cm.nipy_spectral)
ax[1,1].scatter(X[4*z:4*z+c,0:d], Y[4*z:4*z+c,0:d], s=R[0:c,0:d]**2, c=D[4*z:4*z+c,0:d]**.2, cmap=plt.cm.nipy_spectral)
plt.savefig("Mercator_Mandelbrot_zoom.png", dpi=100)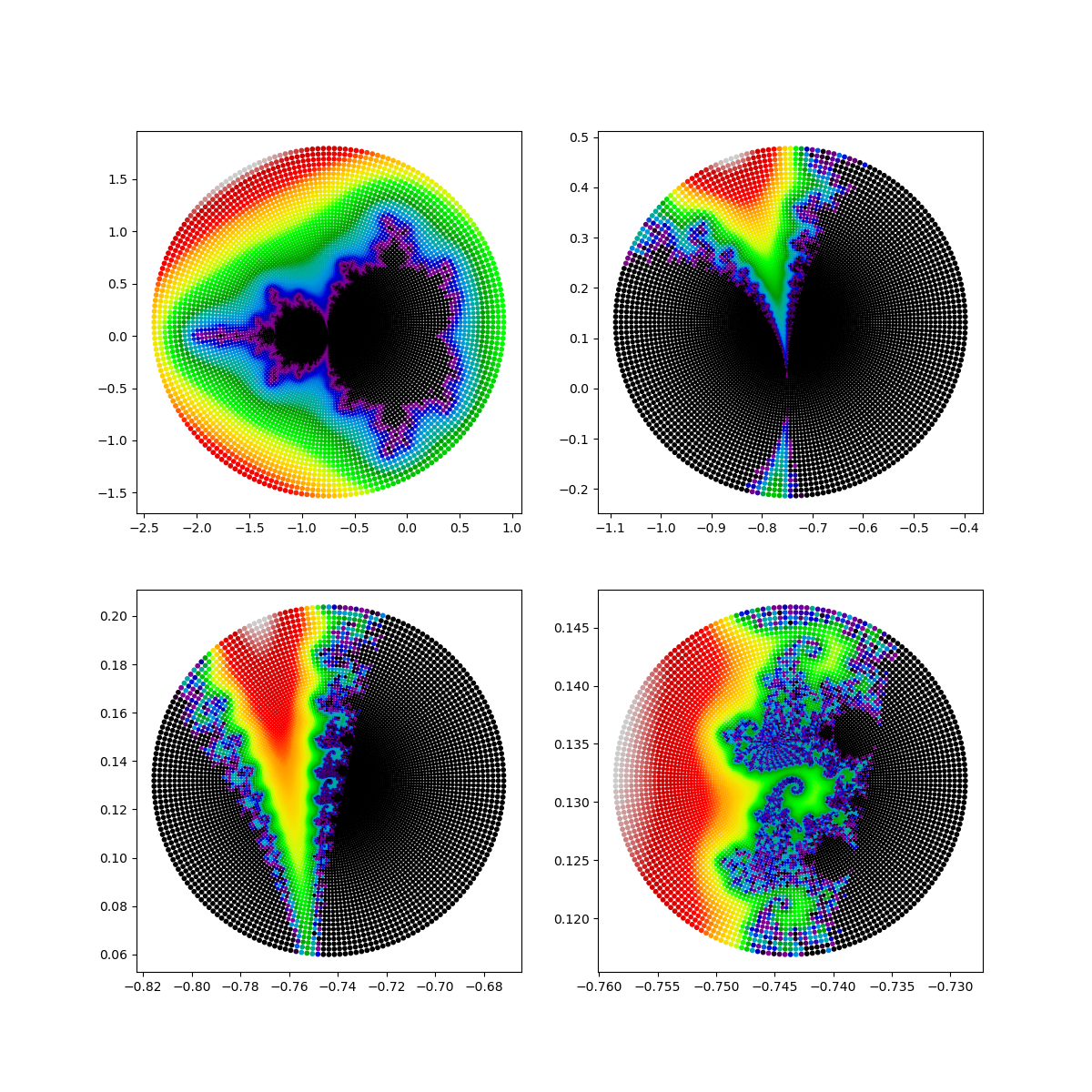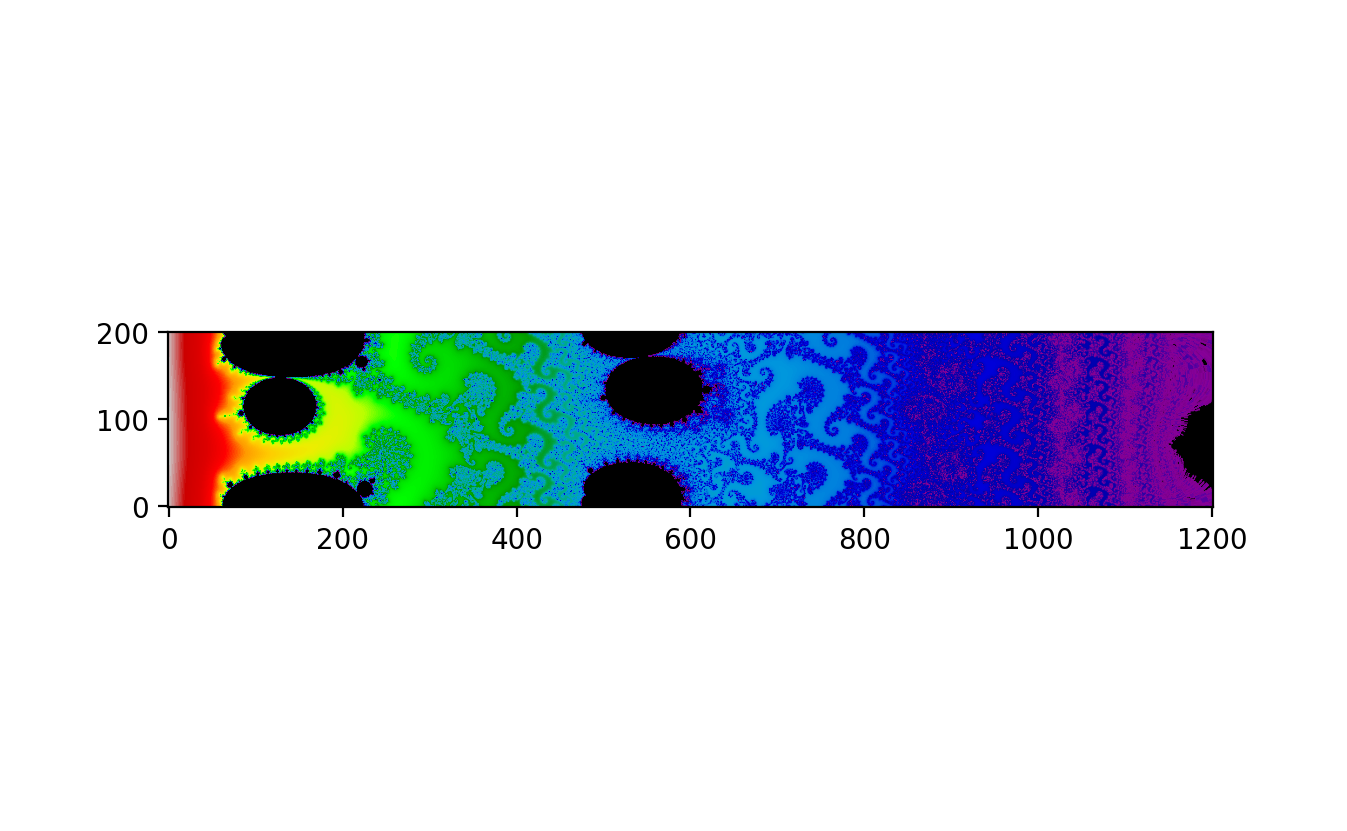

Perturbation Theory and Deep Mercator Maps

For generating deep zoom images of the Mandelbrot set, a highly efficient technique involves calculating a single point with high precision and using perturbation theory to approximate all other points. This approach significantly reduces the computational burden while maintaining the accuracy of the fractal’s intricate details.

Mathematical Insight

Perturbation Theory: Perturbation theory is a set of approximation schemes directly related to small changes in the known solutions of a problem. When applied to the Mandelbrot set, this theory allows us to use the high-precision calculation of a single point to estimate the behaviour of nearby points with standard accuracy. The primary advantage is that it minimizes the need for high-precision calculations across the entire image, which would otherwise be computationally prohibitive.

\[ z_{n+1}=z^2_n+c \]

In the context of perturbation theory, the initial point \(z\) is calculated with high precision. Then, small perturbations \(\delta z\) are applied to approximate the positions of other points. The corrections needed to account for these perturbations are typically small, which makes this approach efficient.

Rebasing: As the zoom level increases, small numerical errors can accumulate, potentially leading to glitches in the rendered image. Rebasing is a technique used to mitigate these errors. It involves periodically recalculating the base high-precision point and resetting the perturbation calculations to this new base. This step ensures that any accumulated errors are corrected, thereby maintaining the integrity of the deep zoom visualization.

Code 
# Perturbation Theory and Deep Mercator Maps

import numpy as np
import matplotlib.pyplot as plt

import decimal as dc  # decimal floating point arithmetic with arbitrary precision
dc.getcontext().prec = 80  # set precision to 80 digits (about 256 bits)

d, h = 50, 1000  # pixel density (= image width) and image height
n, r = 80000, 100000  # number of iterations and escape radius (r > 2)

a = dc.Decimal("-1.256827152259138864846434197797294538253477389787308085590211144291")
b = dc.Decimal(".37933802890364143684096784819544060002129071484943239316486643285025")

S = np.zeros(n+1, dtype=np.complex128)
u, v = dc.Decimal(0), dc.Decimal(0)

for k in range(n+1):
    S[k] = float(u) + float(v) * 1j
    if u ** 2 + v ** 2 < r ** 2:
        u, v = u ** 2 - v ** 2 + a, 2 * u * v + b
    else:
        print("The reference sequence diverges within %s iterations." % k)
        break

x = np.linspace(0, 2, num=d+1, dtype=np.float64)
y = np.linspace(0, 2 * h / d, num=h+1, dtype=np.float64)

A, B = np.meshgrid(x * np.pi, y * np.pi)
C = 8.0 * np.exp((A + B * 1j) * 1j)

E, Z, dZ = np.zeros_like(C), np.zeros_like(C), np.zeros_like(C)
D, I, J = np.zeros(C.shape), np.zeros(C.shape, dtype=np.int64), np.zeros(C.shape, dtype=np.int64)

for k in range(n):
    Z2 = Z.real ** 2 + Z.imag ** 2
    M, R = Z2 < r ** 2, Z2 < E.real ** 2 + E.imag ** 2
    E[R], I[R] = Z[R], J[R]  # rebase when z is closer to zero
    E[M], I[M] = (2 * S[I[M]] + E[M]) * E[M] + C[M], I[M] + 1
    Z[M], dZ[M] = S[I[M]] + E[M], 2 * Z[M] * dZ[M] + 1

N = abs(Z) > 2  # exterior distance estimation
D[N] = np.log(abs(Z[N])) * abs(Z[N]) / abs(dZ[N])

plt.imshow(D.T ** 0.015, cmap=plt.cm.nipy_spectral, origin="lower")
plt.savefig("Mercator_Mandelbrot_deep_map.png", dpi=200)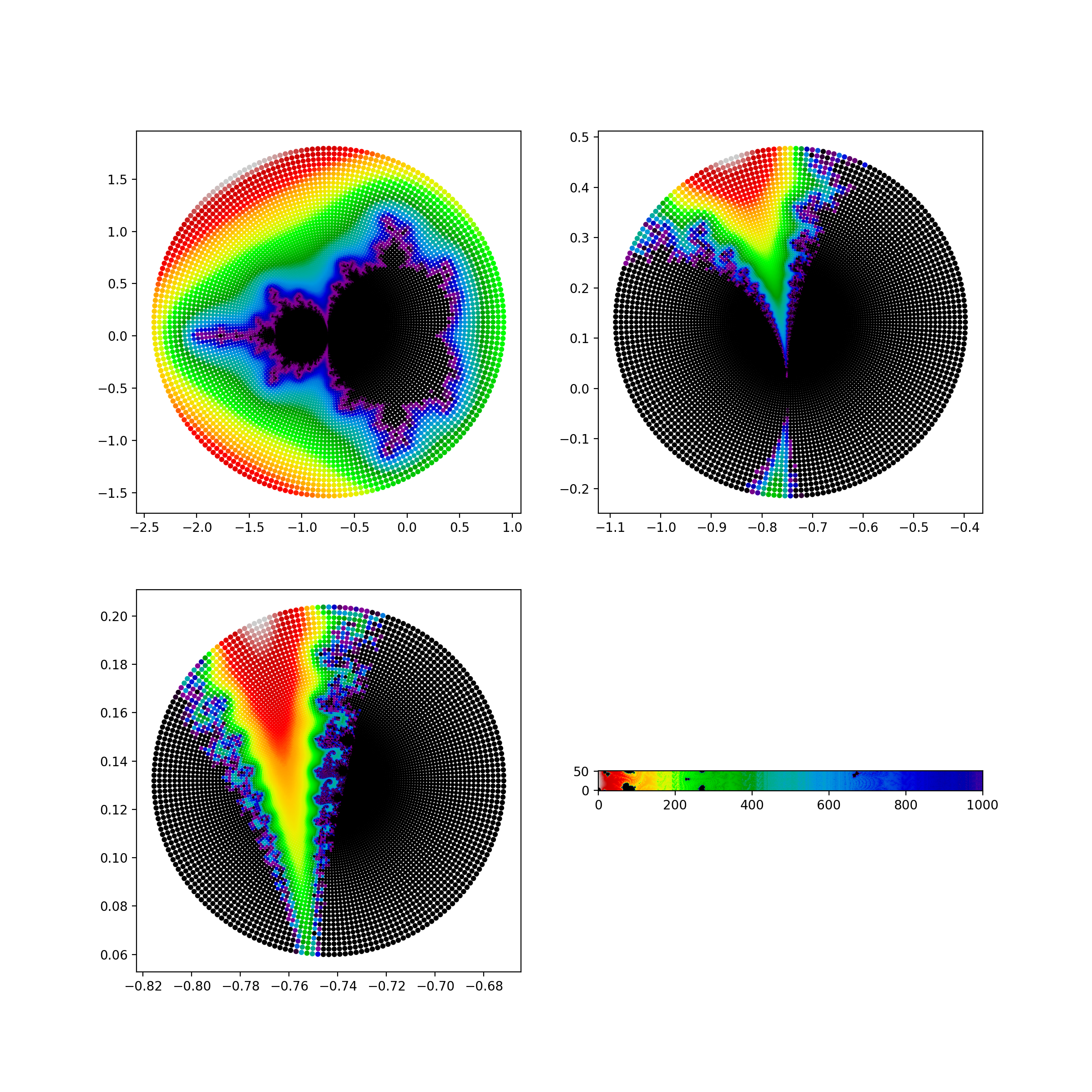

Advanced Techniques in Mandelbrot Set Visualization

The Mandelbrot set, a cornerstone of fractal geometry and complex dynamics, has been the subject of extensive research and visualization techniques. Through various methods, researchers have enhanced our ability to explore and understand this intricate set. The advanced techniques discussed here—Normalization, Distance Estimation, Boundary Detection, Normal Map Effect, Stripe Average Coloring, Mercator Projection, and Perturbation Theory—each contribute uniquely to the visualization and exploration of the Mandelbrot set.

Integrating Techniques for Comprehensive Exploration

By integrating these advanced visualization techniques, researchers can explore the Mandelbrot set in ways that were previously unimaginable. Normalization, distance estimation, and boundary detection provide the groundwork for accurate and detailed images. The Normal Map Effect and Stripe Average Coloring add depth and highlight complex patterns. Mercator projection and perturbation theory enable deep zoom explorations, revealing the fractal’s infinite complexity at various scales.

These techniques collectively push the boundaries of fractal visualization, allowing for a deeper understanding and appreciation of the Mandelbrot set. As computational methods and visualization tools continue to advance, we can expect even more detailed and insightful explorations of this fascinating mathematical object. The work of researchers like Jussi Härkönen, Arnaud Chéritat, David Madore, and Anders Sandberg exemplifies the innovative approaches that drive this field forward, opening new avenues for both mathematical research and artistic expression.

Connection with the Mandelbrot Locally Connected Conjecture (MLC)

The MLC conjecture suggests that no matter how much you zoom into the Mandelbrot set, it will always appear as one connected piece. The tools and techniques mentioned above play a significant role in exploring and visualizing this conjecture:

  1. Normal Map Effect: Enhances the visual details of the Mandelbrot set, making it easier to see the connections and structures within the set at various zoom levels.

  2. Mercator Projection: Offers ways to represent and analyze different sections of the complex plane, aiding in understanding the global and local structure of the Mandelbrot set.

  3. Deep Zoom Images: Enable continuous and detailed examination of the Mandelbrot set, which is essential for investigating its local connectivity properties.

Conclusion

Using advanced visualization techniques such as the normal map effect, projections like Mercator, and deep zoom images allows for a better exploration and understanding of the Mandelbrot set. These tools help in visualizing the complex, detailed structures of the set and are essential in investigating mathematical properties such as local connectivity. This local connectivity question, if it can be solved, will give us almost complete control and understanding of the Mandelbrot set. The hope is that once we fully comprehend quadratic polynomials, we can extend our insights to more complicated dynamical systems and describe them in greater detail. However, a complete understanding of the Mandelbrot set would not diminish our collective fascination with this famous fractal. The richness, complexity, and beauty of the Mandelbrot set continue to inspire and captivate mathematicians and enthusiasts alike, ensuring its lasting allure and significance in the realm of mathematics.

Further Readings

The Quest to Decode the Mandelbrot Set, Math’s Famed Fractal

Related Article

  1. The Map of Mathematics

  2. In Noisy Equations, One Who Heard Music

  3. Dennis Sullivan, Uniter of Topology and Chaos, Wins the Abel Prize

  4. A Brazilian Wunderkind Who Calms Chaos