Mathematical Induction-II

“Eliminate all other factors, and the one which remains must be the truth.” ~Sherlock Holmes (The Sign of Four)

In the previous episode of Mathematical Induction-I, we discussed the philosophy of mathematical induction, introduced the basic idea of mathematical induction, and solved some problems. In this episode of mathematical induction first, we’ll recall the concept of mathematical induction and then we’ll discuss the more interesting problem and their solution strategies.

Recalling The Philosophy of Mathematical Induction

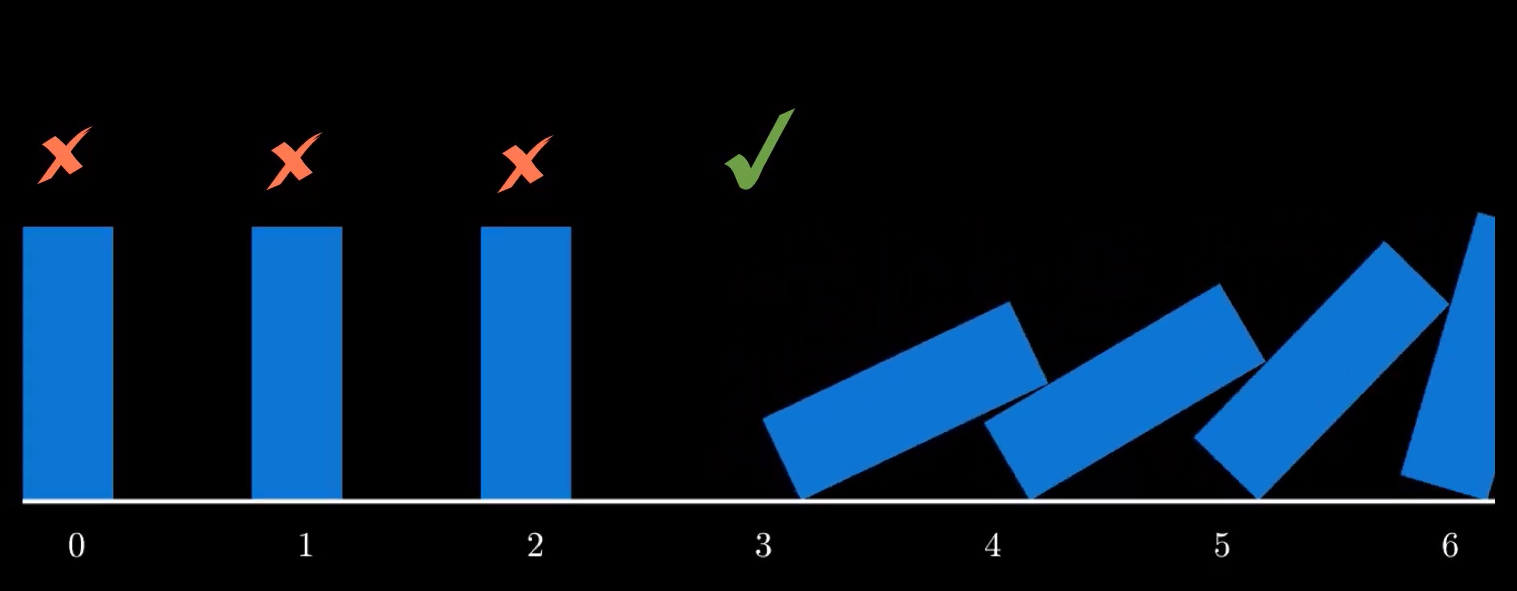
Domino Toppling

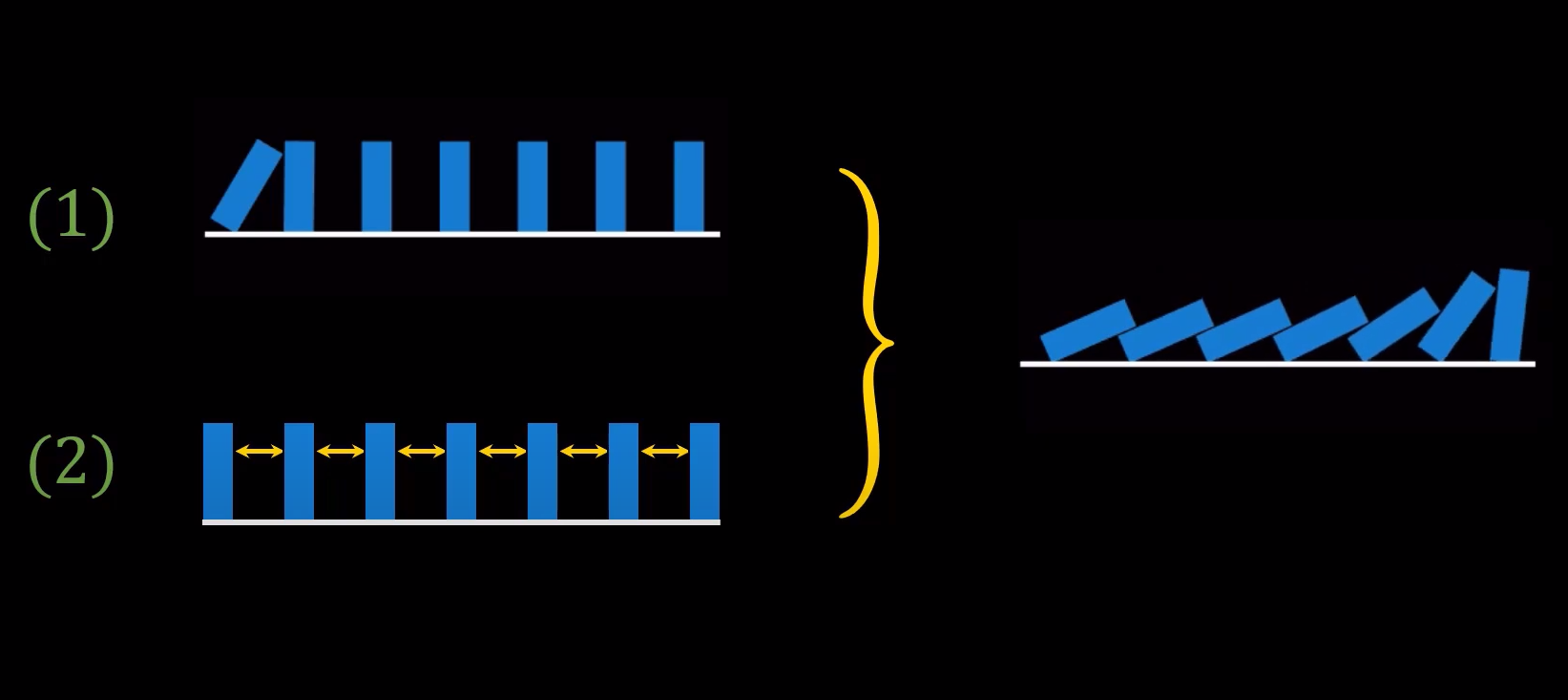
Mathematical induction is like a domino effect. The domino effect is a chain reaction that occurs when one event sets off a series of similar, related, or connected events. It is a reference to a series of standing dominoes, each of which topples the next, creating a chain reaction.

You may be familiar with the term called ‘Domino Toppling’. Domino toppling is achieved by standing dominoes on end and arranging them in the desired patterns and sequences. Such a sequence is called a domino run and then triggers the first one in line to create a chain reaction also called the domino effect. Mathematical Induction uses this principle to prove certain properties.

Mathematical & Logical Perspective

Let $P_n$ be a property that depends on a certain number $n.$ For example,${\displaystyle P_n:\text{Tile number}n}$ $\text{falls}$The steps will prove by induction are the following.

${\displaystyle P_n:\text{Tile number}n\text{falls}}$

1. Check $P_0$ is true. ( The first tile falls.)

2. $\mathrm{\forall }n\in \mathbb{N}n\ge 0$ assumes $P_n$ is true and proves $P_{n+1}$ also true. (if a tile falls it pushes the next. )

Here step 1 is called the base case and step 2 is the induction step. After completing these two steps we can conclude that $P_n$ is true for all natural numbers $n$.

Now a question can arise How come we assume that $P_n$ is true when this is what we want to prove?

The answer i.e., there are two completely different things $\mathrm{\forall }n\in \mathbb{N},P_n$ is true, meaning all the tiles fall which is our final target. On the other side, we have $\mathrm{\forall }n\in \mathbb{N},P_n⟹P_{n+1}$ also true, which means that if a tile falls it causes the next one to fall. This does not necessarily means that the tile number $n$ falls.

More generally saying that $A⟹B$ we are not saying that $A$ is true or $B$ is true. We are just saying if ever $A$ is true then $B$ is also true or the implication is true.

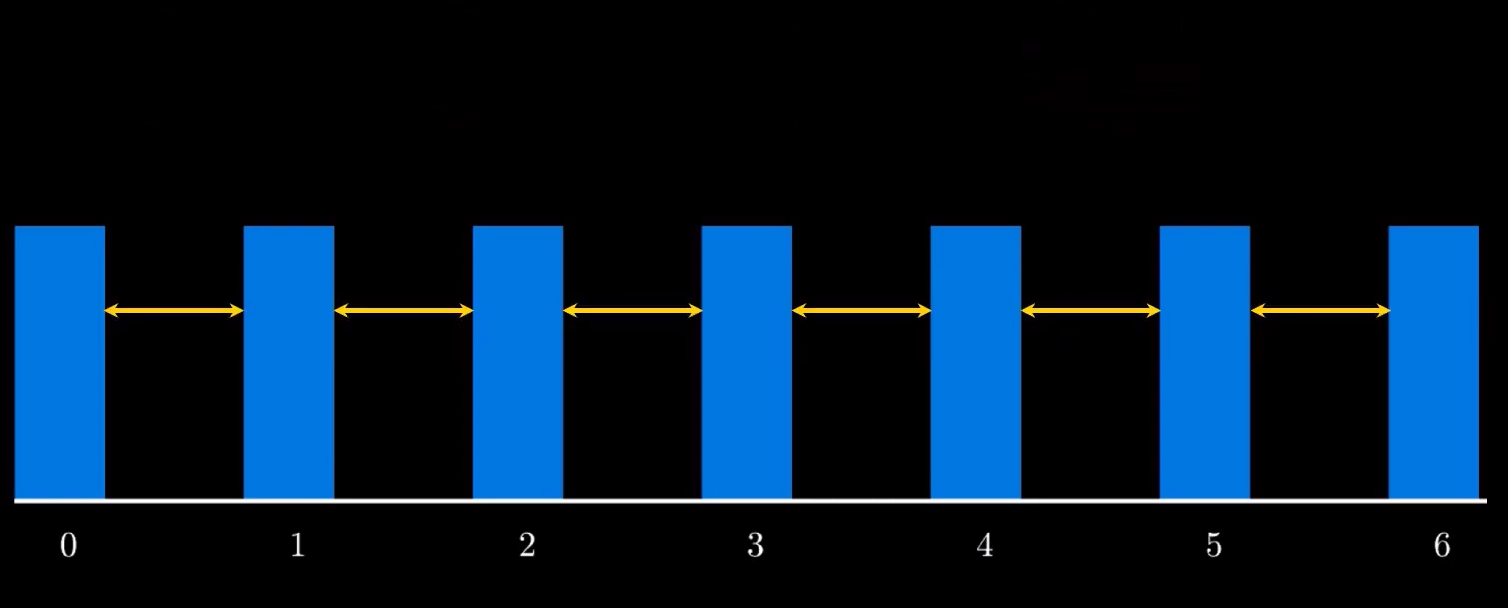
In the case of dominoes, we do not need to push a tile to see if it causes the next one to fall. All we need to prove is that the tiles are close enough so that the implication and therefore the induction step is satisfied. If the first tile falls and the distance between the tiles is small then all

the tiles fall or more formally $P_0$ and $\mathrm{\forall }n\in \mathbb{N},P_n⟹P_{n+1}$ together imply that $\mathrm{\forall }n\in \mathbb{N},P_n.$

Now, we’ll discuss a few special examples to help you better understand mathematical induction

Problem Solving

Objective Type Question

Q1. Prove using mathematical induction that $P_n:2^n\ge n+5\mathrm{\forall }n\in \mathbb{N}$

$$P_n:2^n\ge n+5$$

$$P_{n+1}:2^{n+1}\ge n+6$$

$$\text{If}{P}_n\text{is true, means}{2}^n\ge n+5⟹2^{n+1}\ge 2n+10\ge n+6$$

$$\therefore 2^{n+1}\ge n+6\mathrm{\forall }n\in \mathbb{N}$$

Therefore, the induction step is valid for any natural number $n.$ So, we can claim that,

$$\boxed{{\displaystyle P_n⟹P_{n+1}}}$$

Hence, $P_n:2^n\ge n+5\mathrm{\forall }n\in \mathbb{N}$ is true.

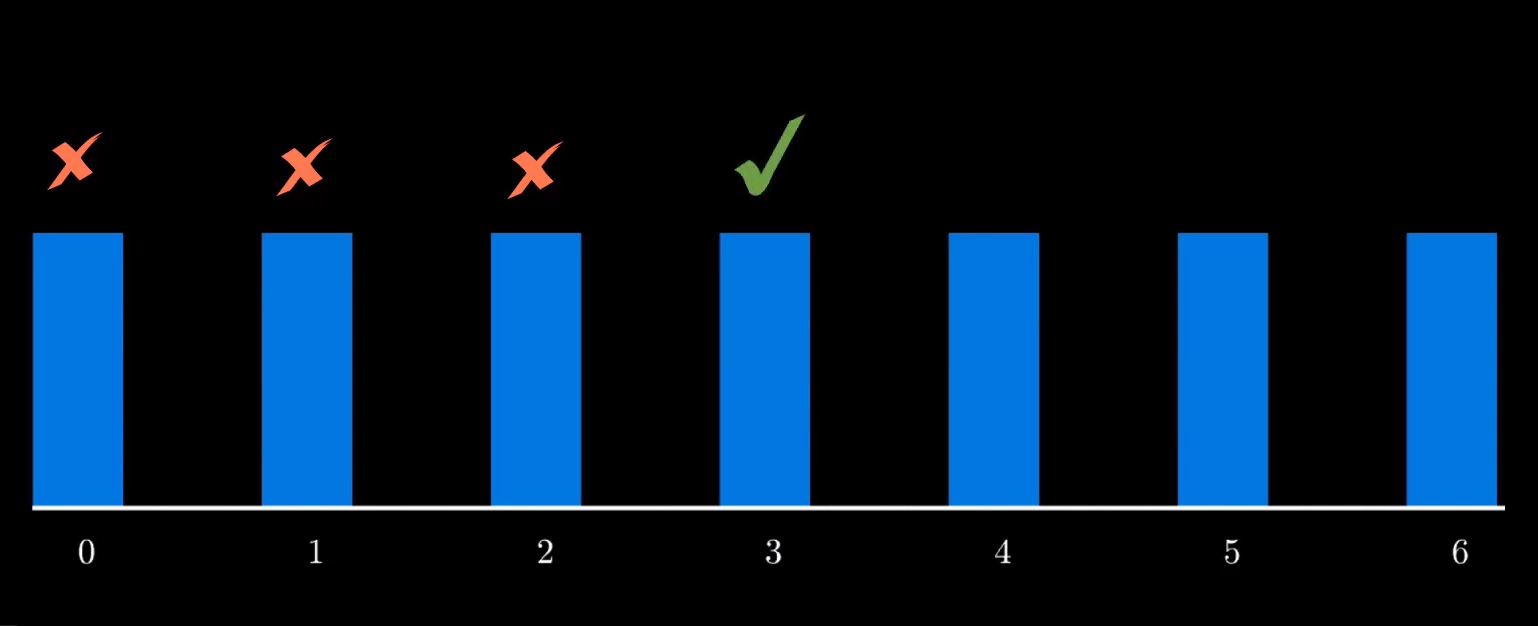
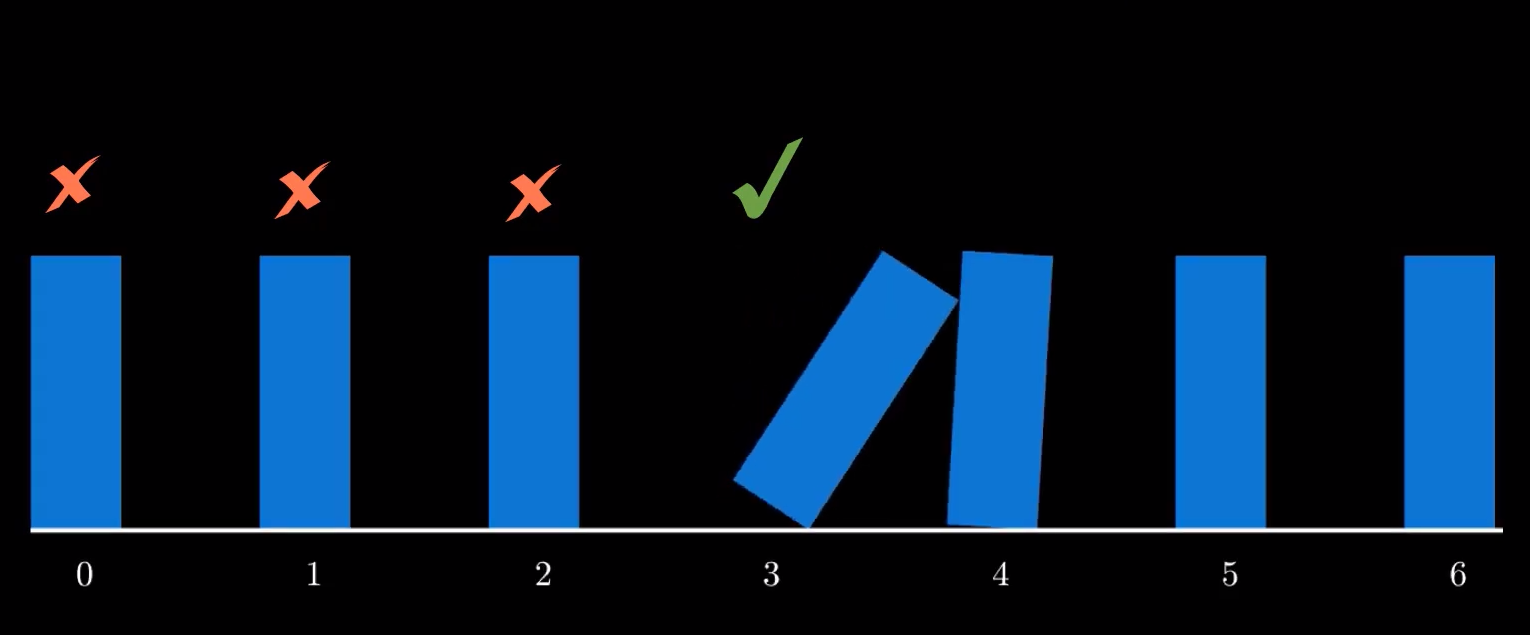
The domino tiles are close to each other. However neither $P_0,P_1\text{nor}{P}_2$ is true. The above property is true only starting from $3$. The base case here is $3$. Adding the induction step we conclude that $P_n$ is true only $n\ge 3.$ Tile $0,1$ and $2$ remain upright the others fall one after the other starting from $3.$

Q2. Show that the property holds $P_n:n\in \mathbb{R}\mathrm{\setminus }\mathbb{Q}$

Here, $P_n:n\in \mathbb{R}\mathrm{\setminus }\mathbb{Q}$ means $n$ belongs to $\mathbb{R}-\mathbb{Q}$ where $\mathbb{R}-\mathbb{Q}=\{x|x\in \mathbb{R},x\notin \mathbb{Q}\}$ i.e., $n$ is an irrational number. If $n$ is not rational, then adding $1$ won’t make the result rational. Therefore, $n+1$ also irrational.

$$n\in \mathbb{R}\mathrm{\setminus }\mathbb{Q}⟹(n+1)\in \mathbb{R}\mathrm{\setminus }\mathbb{Q}$$ Therefore, $P_n$ does imply $P_{n+1}$.

Try Yourself

1. Prove using mathematical induction that $2^n\ge 5n-8$

2. Prove using mathematical induction that $n+1\ge 2^{n-4}$

Subjective Type of Question

Dealing Inequality Condition

1. $\text{Prove that}{\displaystyle {\displaystyle \frac{(2n)!}{(n!{)}^2}}>{\displaystyle \frac{4n}{2n+1}}\mathrm{\forall }n\in \mathbb{N}}$

   Solution:

   $\text{Consider}$ $\text{that}$ $n$ $\text{is a natural number and given that}$ $P_n$ $\text{is true}$

   $$\therefore P_n:{\displaystyle \frac{(2n)!}{(n!{)}^2}}>{\displaystyle \frac{4n}{2n+1}}$$

$\text{Now,}n=1\text{then, L.H.S = }\frac{2!}{(1!{)}^2}=2\text{and R.H.S =}\frac{4}{2+1}=\frac{4}{3}\therefore \text{L.H.S > R.H.S}$

$\therefore P_1\text{is true}$

$\text{Let us consider}m\text{is a natural number and};P_m\text{is true.}$

${\displaystyle {\displaystyle \frac{(2m)!}{(m!{)}^2}}>{\displaystyle \frac{4m}{2m+1}}\dots \dots (1)}$

$\text{We will prove that,}{P}_{m+1}\text{is also true.}$

${\displaystyle {\displaystyle \frac{\{2(m+1)\}!}{\{(m+1)!{\}}^2}}={\displaystyle \frac{(2m+2)!}{\{(m+1)m!{\}}^2}}={\displaystyle \frac{(2m+2)(2m+1).(2m)!}{(m+1{)}^2(m!{)}^2}}}$

${\displaystyle ={\displaystyle \frac{2(2m+1)}{(m+1)}}.{\displaystyle \frac{(2m)!}{m!}}>{\displaystyle \frac{2(2m+1)}{(m+1)}}.{\displaystyle \frac{4m}{2m+1}}(\text{Getting from the (1))}}$

$={\displaystyle \frac{8m}{m+1}}\dots (2)$

${\displaystyle \text{Now,}{\displaystyle \frac{8m}{m+1}}-\frac{4(m+1)}{2(m+1)+1}=4[\frac{2m}{m+1}-\frac{m+1}{2m+3}]={\displaystyle \frac{4(3m^2+4m-1)}{(m+1)(2m+3)}}>0}$

$$\therefore \boxed{{\displaystyle {\displaystyle \frac{8m}{m+1}}>{\displaystyle \frac{4(m+1)}{2(m+1)+1}}}}$$

$$\text{Getting from (2)}{\displaystyle \frac{\{2(m+1)\}!}{\{(m+1)!{\}}^2}}>\frac{4(m+1)}{2(m+1)+1}$$

$$\therefore P_{m+1}\text{is true when}{P}_m\text{is true}.$$

$${\displaystyle \frac{(2n)!}{(n!{)}^2}}>{\displaystyle \frac{4n}{2n+1}}\mathrm{\forall }n\in \mathbb{N}\text{(Q.E.D)}$$

2. $\text{Prove that}$ ${\displaystyle \sqrt{1}+\sqrt{2}+\sqrt{3}+\dots +\sqrt{n}<n\sqrt{\frac{n(n+1)}{2}}}$

   Solution:

   $$P_n:\sqrt{1}+\sqrt{2}+\sqrt{3}+\dots +\sqrt{n}<n\sqrt{\frac{n(n+1)}{2}}$$

   From the above assertion $P_n$ is true for $n=2$. Now, assume assertion for $m$ i.e.,

   $$P_m:\sqrt{1}+\sqrt{2}+\sqrt{3}+\dots +\sqrt{m}<m\sqrt{\frac{m(m+1)}{2}}$$ As, $m$ goes to $m+1$ then L.H.S increased by $\sqrt{m+1}$ while the R.H.S increased by

   $\sqrt{m+1}<[(m+1)\sqrt{{\displaystyle \frac{(m+1)(m+2)}{2}}}-m\sqrt{{\displaystyle \frac{m(m+1)}{2}}}]\dots (1)$

   ${\displaystyle ⟹1<[(m+1)\sqrt{{\displaystyle \frac{(m+2)}{2}}}-m\sqrt{{\displaystyle \frac{m}{2}}}]\dots (2)}$

   $⟹1<\sqrt{{\displaystyle \frac{(m+2)}{2}}}+m[\sqrt{{\displaystyle \frac{(m+2)}{2}}}-\sqrt{{\displaystyle \frac{m}{2}}}]\dots (3)$

   Symbolizing the expression in $(3)$ above as $1<A+m(B),$ clearly $A>1$ and $B>0.$ Therefore, the inequality asserted in $(2)$ above is established.

   This concludes the induction step. Hence, the original assertion is true, by induction.

3. $\text{Prove that}$ $(1+x{)}^n>1+nx\text{where}n\in {\mathbb{Z}}^{\mathbb{+}}\text{and}n\ge 2;x>-1.$

   Solution:

$P_n:(1+x{)}^n>1+nx,x>-1$

$\text{If}n=2,(1+x{)}^n=(1+x{)}^2=1+2x+x^2>1+2x[\text{because,}{x}^2>0]$ $\therefore P_2\text{is true.}$

$\text{Let us assume,}m\text{is a positive integer and}{P}_m\text{is true when}m\ge 2$

${\displaystyle \therefore (1+x{)}^m>1+mx\dots (1)}$

$\text{We will prove that}{P}_{m+1}\text{is true i.e.,}(1+x{)}^{m+1}>1+(m+1)x.\text{Now}x>-1⟹x+1>0.$

$\text{Multiplying by}1+x\text{both side of (1) and we get;}$

$$(1+x).(1+x{)}^m>(1+x)(1+mx)$$

$$⟹(1+x{)}^{m+1}>1+mx+x+m{x}^2=1+(m+1)x+m{x}^2$$

$$⟹(1+x{)}^{m+1}>1+(m+1)x[\because m{x}^2>0]$$

$\therefore P_{m+1}\text{is true. Hence,}{P}_m\text{is true. So that}{P}_{m+1}\text{is true where}m\ge 2\text{is a positive integer.}$

$\text{Therefore, mathematical induction step proves that, for}n\ge 2\text{and for}n\in {\mathbb{Z}}^{\mathbb{+}}{P}_n\text{is true.}$

$$(1+x{)}^n>1+nx\text{where}n\in {\mathbb{Z}}^{\mathbb{+}}\text{and}n\ge 2;x>-1.(\text{Proved})$$

4. For which $n$ the inequality $2^n>2n+1$ holds?

Solution: Let us assume that $n$ is a natural number and the given inequality can be written as,

$P_n:2^n>2n+1\mathrm{\forall }n\in \mathbb{N}.$ Now $n=1$ $2^n=2$ and $2n+1=2.1+1=3,\therefore$ In this case $2^n>2n+1$ does not hold.

Again, for $n=2$ then $2^2=4$ and $2n+1=2.2+1=5$ In this case $2^n>2n+1$ does not hold.

For, $n=3$ $2^n=2^3=8and2n+1=2.3+1=7.$ Here $2^n>2n+1$ holds.

Let us assume, $m$ is a natural number and $m>3.$ Let, $P_m:2^m>2m+1$ is true. We have to prove that, $P_{m+1}:2^{m+1}>2(m+1)+1$ is true also.

We know that $m>1$ $\therefore 2^m>2\dots (1)$

Again, for $m>3,2^m>2m+1\dots (2)$

Combining $(1)and(2)$ we get that ,

$$2^m+2^m>2+2m+1$$ $$⟹{2.2}^m>2m+3⟹2^{m+1}>2(m+1)+1$$

Therefore, $P_{m+1}$ is true when $P_m$ is true and $m>3$. So, following principle of mathematical induction $P_n$ is true i.e., the inequality holds while $n\ge 3.$

Hence, $2^n>2n+1$ inequality holds while $n\in \mathbb{N},\mathrm{\forall }n\ge 3.$

Try Yourself

1. $\text{Prove that,}{\displaystyle \frac{(2n)!}{2^{2n}(n!{)}^2}}\le {\displaystyle \frac{1}{(3n+1{)}^{1/2}}}\mathrm{\forall }n\in \mathbb{N}$

2. ${\displaystyle \mathrm{\forall }n\in \mathbb{N}\text{where}n>1\frac{1}{n+1}+\frac{1}{n+2}+\dots +\frac{1}{2n}>\frac{13}{24}}$

3. For $n>1$ prove that ${\displaystyle (\genfrac{}{}{0ex}{}{2n}{n})>\frac{4^n}{n+1}}$

4. If $n\ge 2$ then show that ${\displaystyle 1+\frac{1}{4}+\frac{1}{9}+\dots +\frac{1}{n^2}<2-\frac{1}{n}}$

5. If $n$ is an integer and $n\ge 3$ then show that $2n+1<2^n$

6. For $n\ge 4$ prove that $n^2<n!$

Divisibility Problem

1. $\text{If}n\text{is a even positive integer then prove that,}{x}^n-y^n\text{is divisible by}x+y.$

Solution: $\text{Let us assume,}n=2m;m=1,2,3,4\dots$

$P_m:x^{2m}-y^{2m}\text{will be divisible by}x+y\text{where}m\text{ is a positive integer.(We have to prove)}$

$\text{For}m=1,x^{2m}-y^{2m}=x^2-y^2=(x+y)(x-y)\text{is divisible by}(x+y).\text{Therefore,}{P}_1\text{is true.}$

$\text{Let us assume}t\text{is a positive integer and}{P}_t\text{is true i.e.,}{x}^{2t}-y^{2t}\text{is divisible by}(x+y).$

$\text{Now, we have to prove}{P}_{t+1}\text{is true i.e.,}{x}^{2(t+1)}-y^{2(t+1)}\text{is divisible by}(x+y).$

$$x^{2(t+1)}-y^{2(t+1)}=x^{2t+2}-y^{2t+2}=x^{2t}.x^2-y^{2t}.y^2=x^{2t}.x^2-x^{2t}.y^2+x^{2t}{y}^2-y^{2t}.y^2$$ $$=x^{2t}(x^2-y^2)+y^2(x^{2t}-y^{2t})=x^{2t}(x+y)(x-y)+y^2(x^{2t}-y^{2t})$$

$x^{2t}(x+y)(x-y)\text{is divisible by}(x+y).\text{Again, according to our assumption}{x}^{2t}-y^{2t}\text{is divisible}$

$\text{by}(x+y).$

$$\therefore y^2(x^{2t}-y^{2t})\text{is divisible by}(x+y)$$

$x^{2t}(x+y)(x-y)+y^2(x^{2t}-y^{2t})\text{i.e.,}{x}^{2(t+1)}-y^{2(t+1)}\text{is divisible by}(x+y).\text{Hence,}{P}_{t+1}\text{is true.}$

$$\boxed{{\displaystyle P_t\text{is true}⟹P_{t+1}\text{is also true.}}}$$

$\text{Hence, by mathematical induction}$ $P_m$ $\text{is true where m is positive integer}$.

$\therefore$ $x^{2m}-y^{2m}$ $\text{is divisible by}$ $(x+y)$ i.e., $x^n-y^n\text{is divisible by}x+y\text{for}n\text{even positive integer. (Proved)}$

2. Prove that $p^2+p+1|p^{n+1}+(p+1{)}^{2n-1}\mathrm{\forall }n\in \mathbb{N}$

   Solution: $P_n:p^2+p+1|p^{n+1}+(p+1{)}^{2n-1}$

$\therefore n=1,p^{n+1}+(p+1{)}^{2n-1}=p^2+(p+1{)}^{2.1-1}=p^2+p+1,\text{divisible by}{p}^2+p+1$

$\therefore P_1\text{is true.}$

Let us assume, $m$ is a natural number and $P_m$ is true. $\therefore p^2+p+1|p^{m+1}+(p+1{)}^{2m-1}$

Let us assume, $p^{m+1}+(p+1{)}^{2m-1}=k(p^2+p+1)\mathrm{\forall }k\in {\mathbb{Z}}^{\mathbb{+}}$

Now, $p^{(m+1)+1}+(p+1{)}^{2(m+1)-1}=p^{m+2}+(p+1{)}^{m+2}=p^{m+2}+(p+1{)}^{2m-1}.(p+1{)}^2$

$\therefore p^{(m+1)+1}+(p+1{)}^{2(m+1)-1}=p^{m+2}+(p+1{)}^{2m-1}.(p+1{)}^2$

$=p^{m+2}+[k(p^2+p+1)-p^{m+1}](p+1{)}^2$

$=p^{m+2}-p^{m+1}(p+1{)}^2+k(p^2+p+1)(p+1{)}^2$

$=p^{m+1}(p-p^2-2p-1)+k(p^2+p+1)(p+1{)}^2$

$=-p^{m+1}(p^2+p+1)+k(p^2+p+1)(p+1{)}^2=p^2+p+1\{k(p+1{)}^2-p^{m+1}\}$

Hence, $p^{(m+1)+1}+(p+1{)}^{2(m+1)-1}=p^2+p+1\{k(p+1{)}^2-p^{m+1}\}\text{ which is divisible by}{p}^2+p+1$

$\therefore P_{m+1}\text{is true}$

$$\therefore P_m\text{is true}⟹P_{m+1}\text{is true also.}$$

Therefore, mathematical induction principle proves that $p^2+p+1|p^{n+1}+(p+1{)}^{2n-1}\mathrm{\forall }n\in \mathbb{N}$

3. Prove that $25|7^{2n}+(2^{3n-3}){.3}^{n-1}\mathrm{\forall }n\in \mathbb{N}$

   Solution: $P_n:25|7^{2n}+(2^{3n-3}){.3}^{n-1}$

$n=1,7^{2.1}+2^{3.1-3}{.3}^{1-1}=50,\text{divisble by}25.\therefore P_1\text{is true}.$

Now, for $P_m:25|7^{2m}+(2^{3m-3}){.3}^{m-1},m\in {\mathbb{Z}}^{\mathbb{+}}\dots \dots (\ast )$

$P_{m+1}:7^{2(m+1)}+(2^{3(m+1)-3}){.3}^{(m+1)-1}=7^{2m}{.7}^2+2^{3m}{.3}^m$

$=7^{2m}{.7}^2+2^{3m-3}{.2}^3{.3}^{m-1}.3={49.7}^{2m}+2^{3m-3}{.3}^{m-1}.24$

$={49.7}^{2m}+{49.2}^{3m-3}{.3}^{m-1}-{25.2}^{3m-3}{.3}^{m-1}$

$=49(7^{2m}+2^{3m-3}.3^{m-1})-{25.2}^{3m-3}{.3}^{m-1}$

Now, from $(\ast )$ we get that $7^{2m}+(2^{3m-3}){.3}^{m-1}$ is divisible by $25$

$7^{2m}+(2^{3m-3}){.3}^{m-1}=25k,\text{where}k\text{is positive integer.}$

$=49.25k-{25.2}^{3m-3}{.3}^{m-1}=25(49k-2^{3m-3}{.3}^{m-1})$

Therefore it is divisible by $25.$ Hence, $P_{m+1}$ is true.

$$\therefore P_m\text{is true}⟹P_{m+1}\text{is true also.}$$

By applying mathematical induction $P_n$ is true for all $n$ positive integer.

Therefore, $25|7^{2n}+(2^{3n-3}){.3}^{n-1}\mathrm{\forall }n\in \mathbb{N}$ (Proved)

Try Yourself

1. Prove that $576|5^{2n+2}-24n-25\mathrm{\forall }n\in \mathbb{N}$

2. $\text{If}n\text{is a even positive integer then prove that,}{a}^n-b^n\text{is divisible by}a+b.$

3. Use the principle of mathematical induction and prove that

   i) $3|2^{2n}-1,n\ge 1,$ ii) $7|3^{2n+1}+2^{n+2},n\ge 1\mathrm{\forall }n\in {\mathbb{Z}}^{\mathbb{+}}$

4. Using mathematical induction prove that $9|{10}^n+{3.4}^{n+2}+5\mathrm{\forall }n\in \mathbb{N}$

5. Prove that for $n\ge 0,\mathrm{\forall }n\in \mathbb{Z}$ $17|{3.5}^{2n+1}+2^{3n+1}$

Problem

• Using principle of mathematical induction prove that $3|2^{2n}-1$ where $n\in \mathbb{N}wheren\ge 1$

Solution: $P_n:3|2^{2n}-1$ Therefore, $P_1:2^{2.1}-1=4-1=3\text{always divisible by 3}\therefore P_1\text{is true}$

Let us consider $P_m$ is true i.e., if $n=m$ then $P_n$ is true. Therefore, let us consider,

$$P_m:3|2^{2m}-1\mathrm{\forall }n\in \mathbb{N};n\ge 1$$

$$⟹2^{2(m+1)}-1=2^{2m+2}-1=2^{2m}{.2}^2-1$$

$$=4.2^{2m}-1={3.2}^{2m}+(2^{2m}-1)$$

As, $2^{2m}-1\text{always divisible by 3}.$ Therefore it is clear that $2^{2(m+1)}-1\text{always divisible by 3}$

$P_{m+1}:2^{2(m+1)}-1\text{always divisible by 3}\therefore P_{m+1}\text{is true.}$

As, $P_1$ is true and $P_m$ is true therefore $P_{m+1}$ is also true. Therefore, for $n\ge 1$ by induction it is clear that $P_n$ is true.

$$3|2^{2n}-1wheren\in \mathbb{N}wheren\ge 1(Proved)$$

Try Yourself

1. Prove that for $n\in \mathbb{N}17|3^{2n+1}+2^{n+2}$

2. Prove that $6|n(n+1)(2n+1)$ for $n\in \mathbb{N}.$

Problem

1. Using mathematical induction prove that

   $$4+44+444+\dots n\text{no. of terms}=\frac{4}{81}({10}^{n+1}-9n-10)$$

Solution: $P_n:4+44+444+\dots n\text{no. of terms}=\frac{4}{81}({10}^{n+1}-9n-10)$

Therefore, $P_1:\frac{4}{81}({10}^2-9.1-10)=4$ which is true. Therefore, $P_1$ is true.

$P_m:4+44+444+\dots m\text{no. of terms}=\frac{4}{81}({10}^{m+1}-9n-10)$ is true.

Now,

$P_{m+1}:4+44+444+\dots (m+1)\text{no. of terms}$

$=4+44+444+\dots m\text{no. of terms}+444\dots [\text{where 4 is there (m+1) no. of times}]$

$=\frac{4}{81}({10}^{m+1}-9m-10)+444\dots (m+1)\text{no. of times}\dots (\ast )$

$\because 444\dots (m+1)no.oftimes=4+4.10+{4.10}^2+\dots (m+1)no.oftimes=4.\frac{{10}^{m+1}-1}{10-1}=\frac{4}{9}({10}^{m+1}-1)$

$\therefore \text{Form (*) we get that},$

$4+44+444+\dots (m+1)\text{no. of terms}=\frac{4}{81}({10}^{m+1}-9m-10)+\frac{4}{9}({10}^{m+1}-1)$

$=\frac{4}{81}({10}^{m+1}-9m-10+{9.10}^{m+1}-9)$

$=\frac{4}{81}[{10.10}^{m+1}-9(m+1)-10]$

$=\frac{4}{81}[{10}^{m+2}-9(m+1)-10]$

Therefore, we can see that $P_{m+1}$ statement is true. So, we can see that $P_1$ is true. As, $P_m$ statement is true then $P_{m+1}$ is true. Hence, by principle of mathematical induction we can say that $P_n$ is true. Therefore,

$$4+44+444+\dots n\text{no. of terms}=\frac{4}{81}({10}^{n+1}-9n-10)(Proved)$$

Try Yourself

1. Using mathematical induction prove that

   $$6+66+666+6666+\dots n\text{no. of terms}=\frac{2}{27}({10}^{n+1}-9n-10)$$

2. Using principle of mathematical induction show that

   $$.7+.77+.777+\dots n\text{ no. of terms}=\frac{7n}{9}-\frac{7}{81}(1-\frac{1}{{10}^n})$$

Conclusion

The Induction Principle is of great importance in all of the fields of mathematics. This content is all about those inquisitive students who are trying to understand the basic & fundamental concepts of higher mathematics but are unable to grasp the insight behind induction principle.

In my previous Mathematical Induction-I I have tried to deliver a coherent understanding and a philosophical overview of Principle of Mathematical Induction. Here, I’ve discussed the mathematics behind principle of mathematical induction and some school level problem which we often deal with.

In a single content, it is not possible to cover all the necessary problem-solving strategies which is also required further. That’s why I’m willing to discuss lots more problems and problem-solving strategies on mathematical induction in my upcoming content which will be an asset to deal with critical problems from INMO, IMO, PUTNUM.

See Also

• Mathematical Induction-I