Unpacking Laurent Expansions in Complex Analysis
A Deep Exploration of Analytic Structure, Principal Parts, and Convergence Domains
Introduction
In complex analysis, one of the most powerful tools for understanding functions near singularities is the Laurent series. While the Taylor series expresses a function as an infinite sum of non-negative powers of \((z-z_0),\) the Laurent series extends this idea by allowing negative powers as well. This extension is not merely technical — it is essential when dealing with functions that are not analytic at certain points but are analytic in an annular region around them.
The concept was introduced in 1843 by the French mathematician Pierre Alphonse Laurent, who showed that many complex functions that cannot be represented by a Taylor expansion (because of singularities) can still be expressed as a convergent series if negative powers are included. In this way, the Laurent series generalized Taylor’s idea, opening the door to the modern theory of residues and singularities. Generally, if a function \(f(z)\) is analytic in an annulus
\[ R_1 < |z-z_0| < R_2,\]
then it can be expressed as,
\[f(z) = \sum_{n=-\infty}^{\infty} a_n (z-z_0)^n,\]
where the terms with \(n \geq 0\) form the analytic part, and those with \(n < 0\) form the principal part. The Laurent series is particularly significant because:
It naturally describes functions around isolated singularities.
The coefficient \(a_{-1}\) corresponds to the residue, a cornerstone concept in evaluating complex integrals.
It provides a systematic way to classify singularities as removable, poles, or essential.
An annulus in the complex plane is the open region between two concentric circles centered at some point \(z_0 \in \mathbb{C}.\)
Formally, for \(0 \leq R_1 < R_2 \leq \infty\), the annulus centered at \(z_0\) is defined as:
\[A(z_0; R_1, R_2) = \{ z \in \mathbb{C} \; : \; R_1 < |z - z_0| < R_2 \}\]
Intuition
If \(R_1 = 0\), the annulus reduces to the open disk of radius \(R_2\).
If \(R_2 = \infty\), the annulus becomes the exterior region \(|z-z_0| > R_1.\)
Otherwise, it’s a “ring-shaped” region that excludes the inner circle \(|z-z_0|=R_1\) and outer circle \(|z-z_0|=R_2\).
In this article, we adopt a problem-solving perspective on the Laurent series. We begin with its foundational definition, proceed to examine expansions around various points in the complex plane, and systematically work through illustrative examples.
The Laurent series converges precisely in an annulus.
The inner radius \(R_1\) is determined by the nearest singularity inside,
The outer radius \(R_2\) is determined by the nearest singularity outside.
So, the annulus captures exactly the region where the series is valid.
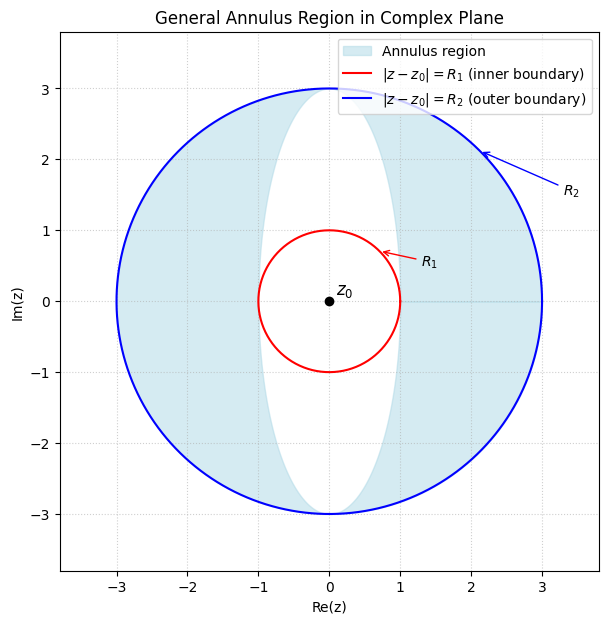
Here’s the geometric illustration of a general annulus in the complex plane:
- The center is at \(z_0\).
- The inner boundary is the circle \(|z - z_0| = R_1\) (red).
- The outer boundary is the circle \(|z - z_0| = R_2\) (blue).
- The shaded ring-shaped region between them is the annulus:
\[A(z_0; R_1, R_2) = \{ z \in \mathbb{C} : R_1 < |z - z_0| < R_2 \}.\]
This is exactly the domain where a Laurent series converges.
By the conclusion, readers will not only master the techniques for computing Laurent series, but also begin to see how these expansions act like X-rays—revealing hidden singularities, symmetries, and the layered anatomy of complex functions that ordinary power series leave untouched.
For readers who wish to explore the concept of an analytic function not only from its theoretical definition but also through rich visual and computational perspectives, please refer to my GitHub repository.
Definition (Laurent Series)
Let \(f(z)\) be a complex function that is analytic in an annulus (a ring-shaped domain)
\[A = \{ z \in \mathbb{C} : r < |z - z_0| < R \}\]
where \(0\leq r < R \leq \infty\). Then \(f(z)\) can be represented as a Laurent series centered at \(z_0\):
\[f(z) = \sum_{n=-\infty}^{\infty} a_n (z - z_0)^n,\] which explicitly splits into two parts:
\[ f(z) = \underbrace{\sum_{n=0}^{\infty} a_n (z - z_0)^n}_{\text{Analytic (Taylor) part}} \; + \; \underbrace{\sum_{n=1}^{\infty} \frac{a_{-n}}{(z - z_0)^n}}_{\text{Principal part}}. \]
\[ \displaystyle \underbrace{\sum_{n=-\infty}^{\infty} a_n = \lim _{N \to \infty}\sum_{n=-N}^{N}a_n}_{\text{Summing terms indexed by all integers n, both positive and negative going out to infinity}} \implies \underbrace{S_N = \sum_{n=-N}^{N}a_n}_{\text{Interprete as limit of partial sums}} \]
So we are adding up contributions from all integer values of \(n\) both \(+ve\) & \(-ve\), extending infinitely in both the directions. The summation is justified if the series \(\displaystyle\sum_{n=-\infty}^{\infty} a_n\) converges absolutely i.e.,
\[ \sum_{n=-\infty}^{\infty} |a_n| < \infty \]
The coefficients \(a_n\) are given by the integral formula:
\[a_n = \frac{1}{2\pi i} \int_{\gamma} \frac{f(\zeta)}{(\zeta - z_0)^{n+1}} \]where \(\gamma\) is a positively oriented simple closed contour lying inside the annulus \(A\).
This sketch offers a poetic visualization of the Laurent series, casting it as a “magical microscope” that reveals the hidden dynamics of complex functions near singularities. On the left, we see a hiker—symbolizing the curious mathematician—standing at the edge of a river, peering through a microscope toward a swirling whirlpool. This whirlpool represents a singularity, a point where the function misbehaves and the Taylor series fails to describe it.
The Laurent series, however, doesn’t shy away from this chaos—it embraces it. By including both positive and negative powers of \(z\), it captures the full spectrum of behavior: the smooth, regular flow around the singularity and the turbulent, swirling motion at its core. The sketch divides this dual nature into two parts: the regular part (positive powers) and the principal part (negative powers), showing how the Laurent series elegantly bridges the calm and the chaotic. It’s not just a tool—it’s a lens that transforms complexity into clarity.
So, Laurent series is just a generalization of Taylor series that allows negative powers, making it suitable to represent functions near singularities.
Explanation of the Definition
- Domain of validity: Unlike Taylor series (which converges only inside a disk), Laurent series is valid in an annulus \(r < |z-z_0| < R.\)
If \(r=0,\) then it reduces to a Taylor series.
If \(r>0,\) the series may include negative powers.
- Two parts of Laurent series:
Analytic part: \(\displaystyle \sum_{n=0}^\infty a_n (z-z_0)^n\), which looks like a Taylor series.
Principal part: \(\displaystyle \sum_{n=1}^\infty \frac{a_{-n}}{(z-z_0)^n}\), which accounts for singularities (poles, essential singularities).
- Utility:
Laurent series is essential for classifying singularities (removable, pole, essential).
Residue theorem uses the coefficient \(a_{-1}\) (called the residue of \(f\) at \(z_0\)).
To deepen the intuition behind the Laurent series, it helps to visualize the geometry of its domain—specifically, the annulus. Imagine a donut-shaped region in the complex plane, centered around a singularity. This annulus lies between two concentric circles: the inner boundary excludes the singularity, while the outer boundary marks the limit of convergence. Within this ring, the Laurent series converges beautifully, weaving together both positive and negative powers of \(z\). The regular part (positive powers) behaves like a Taylor series, capturing smooth variations as you move outward. The principal part (negative powers), however, dives inward, decoding the behavior as you approach the singularity. By sketching this annular domain and labeling the zones of convergence, we see how the Laurent series acts like a bridge—linking the calm exterior with the swirling core. This geometric lens transforms abstraction into clarity, showing not just what the series does, but where and why it works.
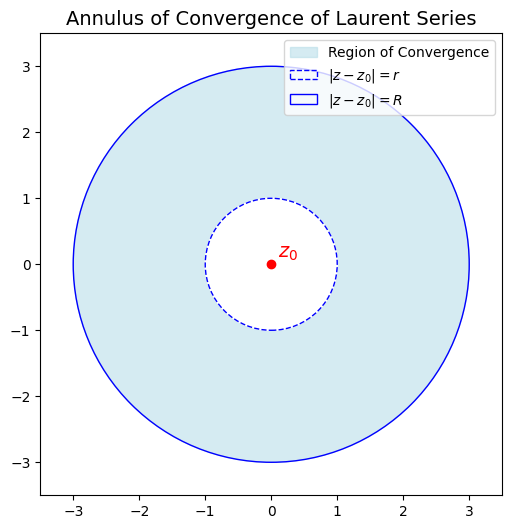
Here’s the geometric intuition for a Laurent series expansion:
- The red dot is the expansion point \(z_0\)
- The dashed inner circle (\(|z-z_0| =r\)) marks where the series cannot cross inward (due to a singularity inside).
- The solid outer circle (\(|z-z_0|=R\)) marks where the series cannot extend outward (due to another singularity or boundary).
- The blue shaded annulus is the region where the Laurent series converges.
So, unlike a Taylor series (which converges only in a disk), a Laurent series converges in a ring-shaped domain.
The Rigorous Criterion
Let \(f\) be a complex function with isolated singularities (for instance a meromorphic or analytic function except at isolated points). Fix a center \(z_0\). Denote by \(S\) the set of singularities of \(f\). Then:
Let
\[ r := \inf\{\, |s-z_0| : s\in S,\; s\neq z_0\ \text{and}\ |s-z_0|<\infty\,\} \]
be the distance from \(z_0\) to the nearest singularity (other than possibly \(z_0\) itself). If \(z_0\) is itself a singularity, put \(R_{\text{inner}}=0\). If there is no singularity at finite distance inside (i.e. \(S\setminus\{z_0\}=\varnothing\)), take \(r=\infty\).
Let
\[ R := \inf\{\, |s-z_0| : s\in S,\; |s-z_0|>0\,\} \]
be the distance from \(z_0\) to the nearest singularity (this is the usual outer radius). If there is no singularity at finite distance, take \(R=\infty\). Then there exists a (unique) Laurent series
\[ f(z)=\sum_{n=-\infty}^\infty a_n (z-z_0)^n \]
which converges for \(r<|z-z_0|<R\). The radius \(r\) and \(R\) are precisely determined by the nearest singularities: the Laurent series cannot converge across a singularity because analyticity would extend past the singularity (contradiction). Conversely, on any annulus free of singularities one may use Cauchy integral formulas on circles \(|z-z_0|=\rho\) (with \(r<\rho<R\)) to produce the coefficients
\[ a_n=\frac{1}{2\pi i}\int_{|\zeta-z_0|=\rho}\frac{f(\zeta)}{(\zeta-z_0)^{n+1}}\,d\zeta, \]
and the resulting power series converges for that annulus (standard proofs use uniform convergence of the geometric series expansions and Cauchy estimates).
Theorem (Annulus of convergence for a Laurent expansion)
Statement.
Let \(f\) be a complex function with isolated singularities and fix a center \(z_0\in\mathbb{C}\). Let
\[S=\{s\in\mathbb C:\ s\ \text{is a singularity of }f\}.\]
Define
\[ R:=inf{ ∣s−z0∣:s∈S},r:=\inf\{\,|s-z_0|:s\in S,\ s\neq z_0\,\}\qquad\text{and}\qquad R:=\inf\{\,|s-z_0|:s\in S\}, \]
with the convention that an infimum over an empty set is \(+\infty\). (If \(z_0\) is itself a singularity put \(r=0.\)) Then there exists a unique Laurent series
\[ f(z)=\sum_{n=-\infty}^{\infty} a_n (z-z_0)^n \]
which converges for every \(z\) with \(r<∣z−z_0∣<R\) .
Moreover the coefficients are given (for any \(\rho\) with \(r<\rho<R\) ) by the Cauchy-type integrals
\[ \boxed{\qquad a_n=\dfrac{1}{2\pi i}\int_{|\zeta-z_0|=\rho}\dfrac{f(\zeta)}{(\zeta-z_0)^{n+1}}\,d\zeta\qquad \forall n\in\mathbb{Z}} \]
Problem Solving
Example Problems
Example 1: Simple Rational Function
Expand the function
\[
f(z) = \frac{1}{z(z - 1)}
\]
into a Laurent series about ( \(z_0 = 0\) ) in two different regions:
Case (a): ( \(|z| < 1\) )
We begin by rewriting the function:
\[ f(z) = \frac{1}{z(z - 1)} = \frac{1}{z} \cdot \frac{1}{z - 1} \]
To expand \(\dfrac{1}{z - 1}\) in the region ( \(|z| < 1\) ), we use the geometric series:
\[ \frac{1}{z - 1} = \frac{-1}{1 - z} = -\sum_{n=0}^{\infty} z^n \quad \text{for } |z| < 1 \]
Substituting back into \(f(z)\) :
\[ f(z) = \frac{1}{z} \cdot \left( -\sum_{n=0}^{\infty} z^n \right) = -\sum_{n=0}^{\infty} z^{n - 1} \]
Explicitly, this becomes:
\[ f(z) = \frac{1}{z} - 1 - z - z^2 - \cdots \quad \text{for } |z| < 1 \]
This is a Laurent series with a principal part term \(\frac{1}{z}\), indicating a simple pole at \(z = 0\).
(b) Region: ( \(|z| > 1\) )
In this region, we manipulate the function differently:
\[ f(z) = \frac{1}{z(z - 1)} = \frac{1}{z} \cdot \frac{1}{z - 1} \]
We rewrite \(\dfrac{1}{z - 1}\) as:
\[ \frac{1}{z - 1} = \frac{1}{z} \cdot \frac{1}{1 - \frac{1}{z}} = \frac{1}{z} \sum_{n=0}^{\infty} \left( \frac{1}{z} \right)^n = \sum_{n=0}^{\infty} \frac{1}{z^{n + 1}} \quad \text{for } |z| > 1 \]
So the Laurent series becomes:
\[ f(z) = \frac{1}{z} \cdot \sum_{n=0}^{\infty} \frac{1}{z^{n + 1}} = \sum_{n=0}^{\infty} \frac{1}{z^{n + 2}} \]
Explicitly:
\[f(z) = \frac{1}{z^2} + \frac{1}{z^3} + \frac{1}{z^4} + \cdots, \quad |z|>1.\]
Here, there is no principal part beyond \(\dfrac{1}{z^2}\), so this expansion is analytic at infinity. This series contains only negative powers of \(z\), forming the principal part of the Laurent expansion in this region.
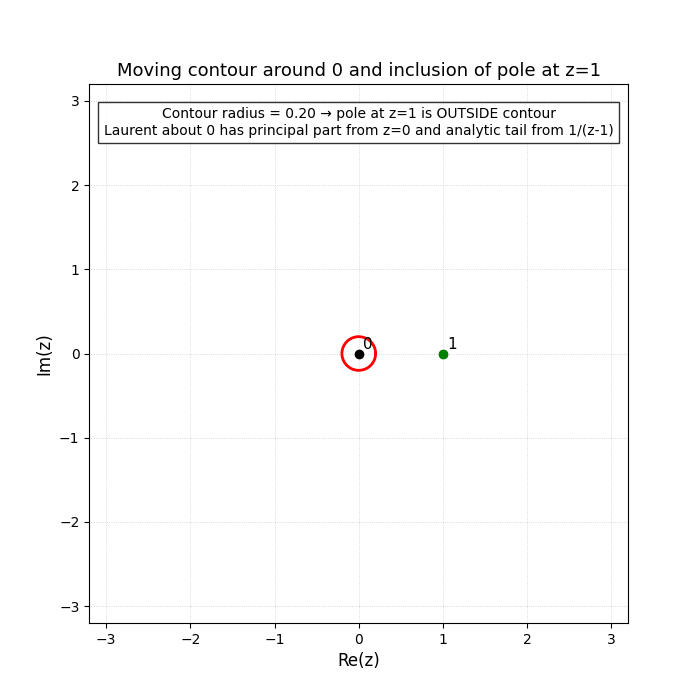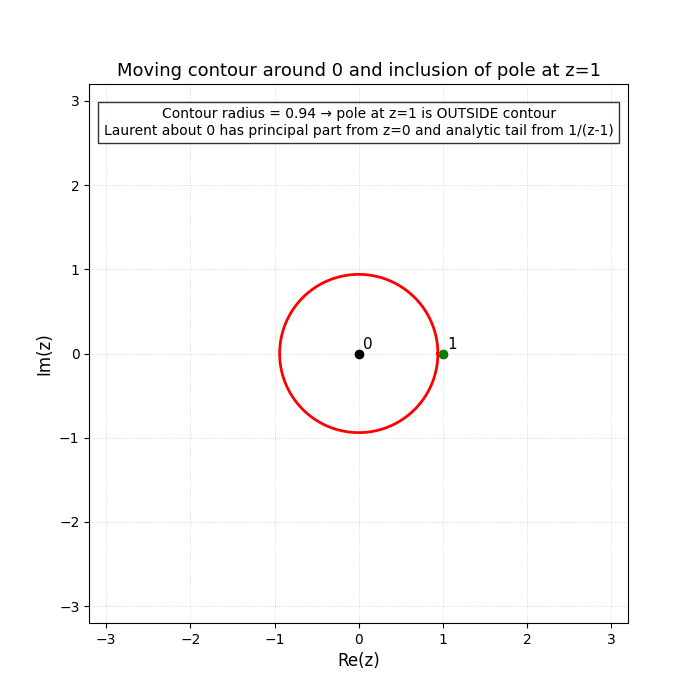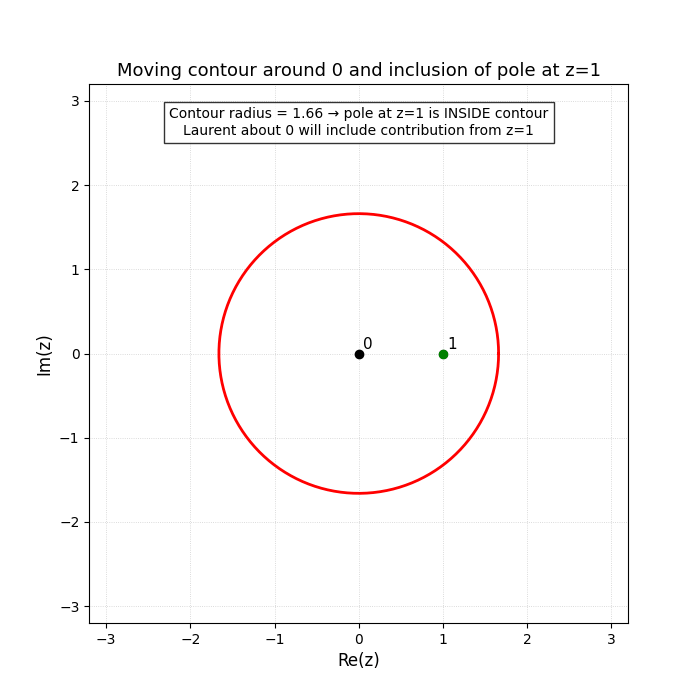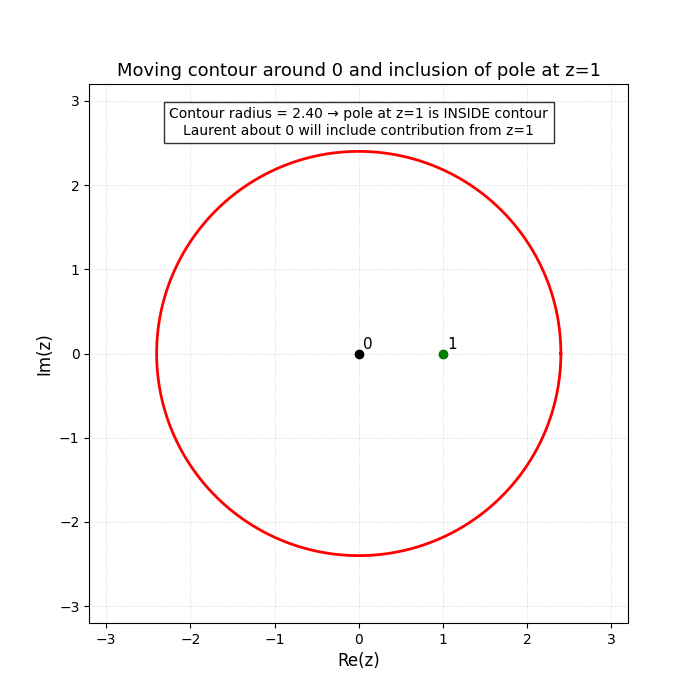
I marked the two expansions of \(f(z)=\dfrac{1}{z(z-1)}\) about \(z_0=0, z=1\) on two diagrams you can see below.
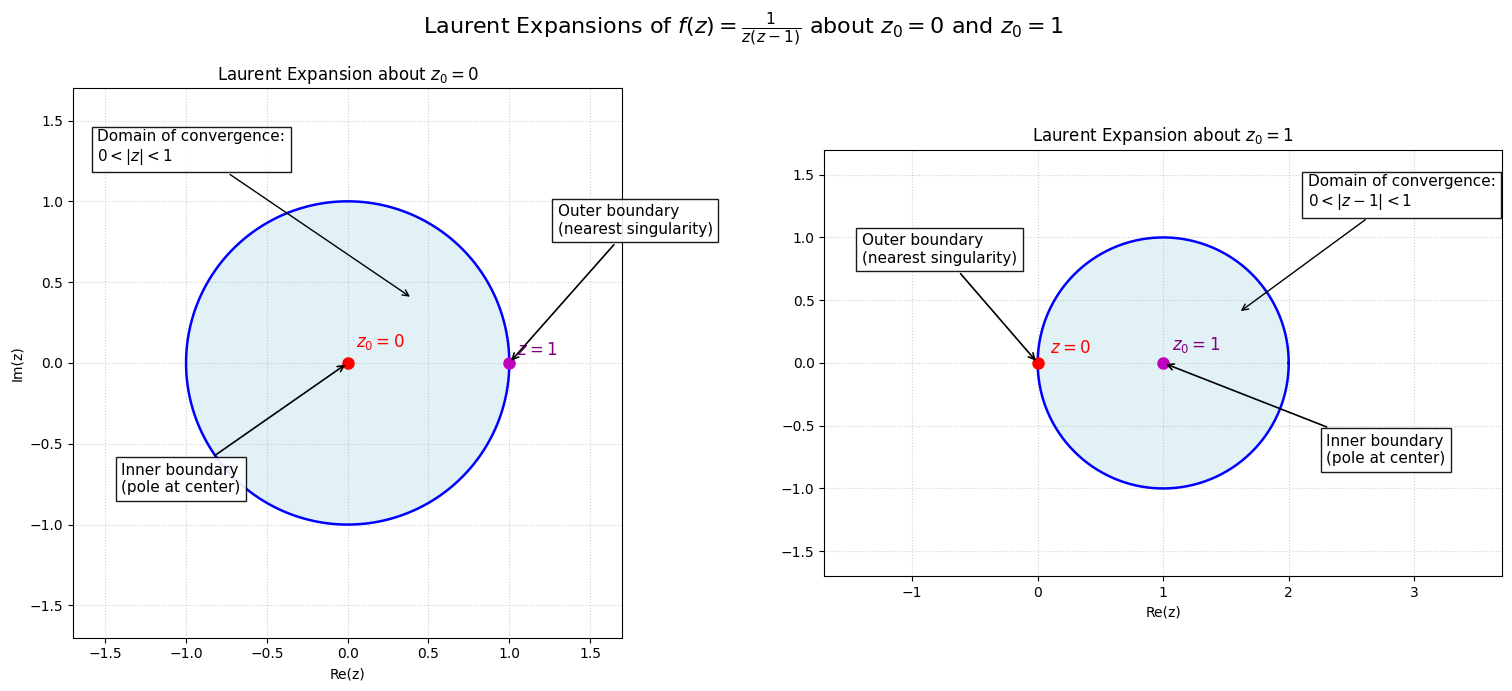
Region \(|z|<1\) (disk)
Laurent expansion (centered at \(0\)) used in the left diagram:
\[f(z)= -\frac{1}{z} - 1 - z - z^2 - \cdots\]
Principal part (negative powers) — boxed on the lower-left of that diagram:
\[-\frac{1}{z} \quad\text{(this gives the residue }a_{-1}=-1)\]
Analytic part (Taylor-like, non-negative powers) — boxed on the upper-right of the diagram:
\[-1 - z - z^2 - \cdots \;=\; \sum_{n=0}^{\infty} (-1)\,z^n.\]
Interpretation: there is one simple pole at \(z=0\) (hence the single \(−1/z\) principal term); the rest is a normal Taylor series valid inside the unit disk.
How we got it quickly:
\[ \dfrac{1}{z-1}=-\dfrac{1}{1-z}=-\sum_{n=0}^\infty z^n \]for \(z∣<1\); multiply by \(1/z.\))
Region \(∣z∣>1\) (exterior)
Laurent expansion (right diagram):
\[ f(z)=\frac{1}{z^2}+\frac{1}{z^3}+\frac{1}{z^4}+\cdots \]
Here there is no analytic (nonnegative-power) part about \(z_0=0\); the expansion consists entirely of negative powers (the principal part relative to the point at infinity / outside the unit circle).
Interpretation: for \(∣z∣>1\) the singularity at \(z=1\) is “outside” the unit disk but the expansion about \(0\) is expressed as a pure tail of negative powers obtained by rewriting \(\displaystyle \dfrac{1}{z-1}=\dfrac{1}{z}\cdot\frac{1}{1-1/z}=\dfrac{1}{z}\sum_{n=0}^\infty \dfrac{1}{z^n}\) and multiplying by \(1/z.\)
For this exploration, we will focus on rigorously computing the structure and behavior of the annulus by delving into the full mathematical details. Rather than relying solely on visual intuition or heuristic descriptions, our aim is to analytically characterize the annular region—its boundaries, the nature of singularities within it, and the corresponding Laurent expansions. This approach will involve precise definitions, careful residue computations at key singular points, and a step-by-step breakdown of how each term in the expansion reflects the geometry and analytic structure of the domain. By grounding our analysis in formal mathematics, we not only clarify the underlying theory but also build a robust foundation for deeper insights into complex function behavior on multiply-connected domains.
Rigorous Computation for \(f(z)=\dfrac{1}{z(z-1)}\; \text{about}\; z_0 = 0\) with More Theoretical Justification
1. Locate the singularities.
The function is rational; its singularities are the zeros of the denominator:
\[ \mathrm{Sing}(f)=\{0,1\}. \]
(There is also a singularity at infinity which matters only for exterior expansions.)
2. Domain of analyticity around \(z_0=0\).
The function is analytic on \(\mathbb{C}\setminus\{0,1\}.\) In a punctured neighborhood of \(0\) the set of points where \(f\) is analytic is
\[ {z : 0<|z|<1 } \cup { z : |z|>1 }. \]
Thus there are two maximal annular regions centered at \(0\) on which \(f\) is analytic:
the punctured disk (inner annulus) \(0<|z|<1\), and
the exterior annulus \(1<|z|<\infty\).
A Laurent series about \(z_0=0\) will exist and converge in each maximal annulus where \(f\) is analytic.
3. Compute the expansions and their radius of convergence.
Inside \(∣z∣<1.\) For \(∣z∣<1\) we rewrite
\[ f(z)=\frac{1}{z(z-1)}=\frac{1}{z}\cdot\frac{1}{z-1}=\frac{1}{z}\cdot\bigg(-\frac{1}{1-z}\bigg) =-\frac{1}{z}\sum_{n=0}^\infty z^n = -\sum_{n=0}^\infty z^{n-1}, \]
where we used the geometric series \(\displaystyle \frac{1}{1-z}=\sum_{n=0}^\infty z^z,\) valid exactly for \(∣z∣<1\). This gives the Laurent series
\[ f(z) = -\frac{1}{z} -1 - z - z^2 - \cdots,\qquad (0<|z|<1). \]
The geometric series converges iff \(∣z∣<1,\) therefore this Laurent expansion converges precisely for \(∣z∣<1.\) The inner radius is \(R_1=0\) (because \(z=0\) itself is a singularity, so the series is on a punctured disk), and the outer radius is \(R_2=1\) (the distance from the center \(0\) to the nearest other singularity \(1\)).
Outside \(∣z∣>1.\) For \(∣z∣>1\) write
\[ \frac{1}{z-1}=\frac{1}{z}\cdot\frac{1}{1-1/z}=\frac{1}{z}\sum_{n=0}^\infty \frac{1}{z^n} \quad(\text{valid for }|1/z|<1\Leftrightarrow |z|>1). \]
Hence
\[ f(z)=\frac{1}{z}\cdot\frac{1}{z-1} =\frac{1}{z^2}\sum_{n=0}^\infty\frac{1}{z^n} =\sum_{n=0}^\infty \frac{1}{z^{n+2}},\qquad (|z|>1). \]
This is a Laurent expansion in negative powers of \(z\) and converges exactly when \(∣z∣>1\). The outer radius for the expansion centered at \(0\) here is \(R_2=\infty\), while the inner radius is \(1\).
Conclusion for \(z_0=0\): the maximal annuli of analyticity (hence convergence) centered at \(0\) are
\[ \boxed{0<|z|<1 \quad\text{(inner Laurent expansion)}} \qquad\text{and}\qquad \boxed{|z|>1 \quad\text{(exterior Laurent expansion).}} \]
If you ask for the Laurent series that represents \(f\) on the region around \(0\) excluding \(0\) but not going past the nearest other singularity, the (principal) annulus of convergence is \(0<|z|<1.\)
In complex analysis, a residue is one of the most important quantities associated with a function near a singularity. When a function becomes unbounded or undefined at a point—called a singularity—the residue extracts the essential numerical information that describes the function’s behavior in the immediate neighborhood of that point.
Compute residues at the simple poles \(z=0\) and \(z=1.\)
At \(z=0\) (simple pole): \(\displaystyle \operatorname{Res}(f,0)=\lim_{z\to 0} z\cdot f(z)=\lim_{z\to0}\frac{1}{z-1}=-1\)
At \(z=1\) (simple pole): \(\displaystyle \operatorname{Res}(f,1)=\lim_{z\to 1}(z-1)\cdot f(z)=\lim_{z\to1}\frac{1}{z}=\;1\)
You can see \(\operatorname{Res}(f,0)=-1\) appears as the coefficient of \(1/z\) in the \(∣z∣<1\) expansion.
For further theoretical development and conceptual clarification, follow my GitHub repository
Conclusion
The Laurent series provides a unified framework for understanding the local behavior of complex functions around singularities. Unlike the Taylor series—which applies only to holomorphic functions—the Laurent expansion naturally accommodates poles and essential singularities by separating the expression into two fundamental components:
the principal part, consisting of negative powers, which encodes the singular behavior and isolates the obstruction to analyticity; and
the analytic part, which behaves identically to a Taylor series and captures the regular, holomorphic contribution.
For a fixed center \(z_0\), different regions in the complex plane may admit different Laurent expansions, depending on the location of surrounding singularities. Inside the unit disk one may obtain both analytic and principal contributions, whereas outside the disk only negative powers remain. This interplay between geometry (the annulus of convergence) and algebra (the structure of the series) is what makes Laurent series a powerful analytic tool.
Ultimately, the Laurent expansion not only extends Taylor’s idea but also lies at the heart of the Residue Theorem, enabling the computation of otherwise intractable contour integrals through the extraction of a single coefficient—the residue. This synthesis of geometric intuition, analytic decomposition, and algebraic structure forms one of the most elegant and useful results in complex analysis.
Readers interested in practicing these concepts are encouraged to attempt the accompanying problem set.
Soft Skills
All visualizations in this article were generated using Python in Google Colab. Click hereto view the notebook.
References
Busam, R. and Freitag, E., 2009. Complex analysis. Springer-Verlag Berlin Heidelberg.
Ablowitz, M. J., & Fokas, A. S. (2021). Introduction to Complex Variables and Applications. Cambridge: Cambridge University Press.