Dynamics of Julia Sets in Rational Maps
Control and Synchronization with Complex Perturbations
Research Intern at Vellore Institute of Technology (VIT-AP University)
Abstract
This paper investigates the dynamics and fractal properties of complex perturbed rational maps defined by the iterative formula zn+1=12(zn+λzqn). It explores the intricate behaviors of Julia sets, emphasizing their geometric and topological features, which reflect the balance between stability and chaos in complex systems. A central focus is the application of the optimal control function method to manipulate Julia sets by treating infinity as a controllable fixed point, thereby stabilizing and shaping their dynamics. Additionally, the paper examines synchronization between Julia sets of distinct systems by incorporating a driving term into the control function, enabling coordinated behaviors. These findings illuminate the interplay between control, synchronization, and fractal geometry, providing insights into complex dynamics and opening pathways for future research in nonlinear systems.
Research Objectives
Study the Dynamics of Julia Sets:
- Analyze the boundary between stability and chaos in perturbed rational maps.
Implement Control Mechanisms:
- Develop and apply an optimal control function to regulate the dynamics of Julia sets.
Investigate the Synchronization of Julia Sets:
- Explore coupling mechanisms to align fractal structures of systems with different parameters.
Visualize Fractal Dynamics:
- Use computational methods, including the escape-time algorithm, to generate and interpret fractal images.
Provide Insights into Chaotic Systems:
- Demonstrate how control and synchronization techniques impact the behavior of complex dynamical systems.
Julia Set in Complex System
The Dynamics of Julia Set
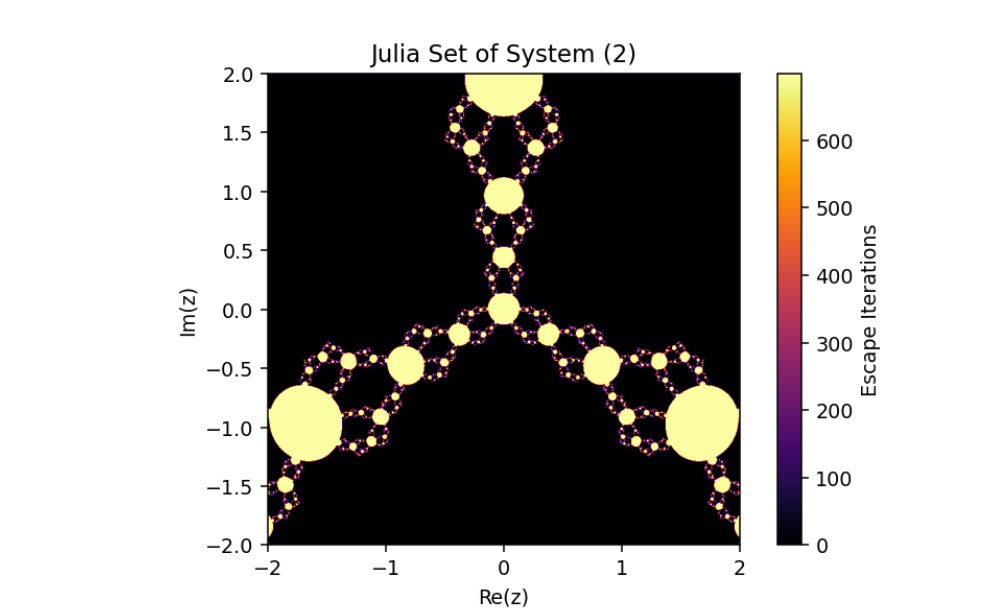
Fractals are widely studied for their ability to model complex phenomena, and Julia sets are prominent fractal structures in complex dynamics. These sets are defined as the closure of repelling periodic points of rational maps. For a rational map R(z)=P(z)Q(z), where P and Q are polynomials with deg(P)>deg(Q), infinity acts as a fixed point, and the Julia set is the boundary of the basin of attraction of infinity. The system zn+1=12(zn+λzqn), studied here, introduces poles at the origin, transforming the dynamics significantly.
A rational map R(z)=P(z)Q(z),whereP(z)andQ(z) are polynomials, forms the basis for studying Julia sets. The degree of R(z) is defined as max(deg(P),deg(Q)). Julia sets are fractal structures and are defined as:
J(R)={z∈C∣the family {Rn(z)}n≥1 is not normal in the sense of Montel}.
Equivalently, J(R) is the closure of the set of repelling periodic points of R(z). For R(z), if |z|→∞, then |R(z)|→∞, making infinity a fixed point. The Julia set J(R) forms the boundary of the basin of attraction of this fixed point.
Proposition
If infinity is an attracting fixed point of R, then there exists S>0 such that |z|>S implies |R(z)|>|z| and |Rn(z)|→∞ as n→∞, for all z satisfying |z|>S.
A Julia set J(R) is a fractal that serves as the boundary between:
Points in the complex plane that exhibit stable, predictable dynamics under a rational map R(z).
Points that diverge to infinity or exhibit chaotic behavior.
In a physical context:
Julia sets often represent systems that alternate between stable and chaotic regimes.
They serve as models for phase transitions, where the boundary represents critical points between phases.
In fields like optics, Julia sets help describe patterns in nonlinear systems, such as wave front distortions or light propagation through media
Dynamics of the Perturbed Rational Map
Perturbed Rational Map:
zn+1=zqn+c+λzpn...(1)
where:
q controls the degree of the polynomial term.
λzpn introduces a singularity (pole) at the origin.
Impact of λ:
For λ=0, the map reduces to the classical form zn+1=zqn+c, a polynomial.
For λ≠0, the pole dramatically changes the system’s dynamics, increasing the map’s degree to p+q and altering the structure of Julia and Mandelbrot sets.
Special Cases:
- When c=0, the study explores how adding a pole affects the Julia set, transforming it from the unit circle (for λ=0 ) to a more complex fractal structure.
The complex perturbed rational map studied is zn+1=12(zn+λzqn), where q≥1, λ∈C, and z∈C. Key features include:
zn+1 contains poles at the origin, altering the dynamics of classical Julia sets.
When λ=0, the system reduces to a polynomial map of degree q+1.
This map generalizes rational maps R(z)=P(z)Q(z), where P(z) and Q(z) are polynomials, by introducing a pole at the origin. This perturbation significantly alters the dynamics and the structure of the Julia sets associated with the map.
In rational maps, fixed points satisfy R(z)=z. The stability of these fixed points depends on the derivative R′(z):
Attracting: R′(z)<1,
Repelling: R′(z)>1,
Neutral: R′(z)=1.
In this work, infinity acts as a fixed point, and its behavior is analyzed through escape criteria and control mechanisms.
Control of Julia Set of the Complex Perturbed Rational System
Control Map & Optimal Control Function
- Definition
- The Base System and Rational Map:
- Introducing the Nonlinear Control:
- Fixed Points and Behavior:
- Escape Criterion:
- Generalized Map:
- Visualization Algorithm: Escape-Time Algorithm
A control parameter k is introduced to modify the dynamics of the map. The controlled map is defined as:
g(z)=f(z)−k⋅(f(z)−z)
Interpretation:
Base Map Contribution: The term f(z) represents the original rational Julia map.
Feedback Control: The term k⋅(f(z)−z) acts as a damping factor. The control parameter k (with 0≤k≤1) adjusts the extent to which the new value depends on the previous iteration.
When k=0, g(z)=f(z), recovering the original Julia map. When k=1, the map becomes stationary.
The base system is:
zn+1=fλ,q(zn)=12(zn+λzqn)...(2)
which can also be written as:
fλ,q(z)=zq+1+λ2zq.
This is a rational map where:
The numerator P(z)=zq+1+λ,
The denominator Q(z)=2zq.
To control the dynamics, a nonlinear control term un is introduced:
un=−k[fλ,q(zn)−zn].
The controlled system becomes:
zn+1=fλ,q(zn)+un
or equivalently:
zn+1=fλ,q(zn)−k[fλ,q(zn)−zn]
Substitute fλ,q(zn)=12(zn+λzqn) into the controlled system:
zn+1=12⋅(zn+λzqn)−k⋅[12⋅(zn+λzqn)−zn]...(3)
This is a concise symbolic representation called controlled rational map, and we define this following way:
R(z)=(1+k)zq+1n+λ(1−k)2zqn
Fixed Points: The fixed points are solutions of R(z)=z, which reduce to solving:
(1+k)zq+1+(1−k)λ2zq=z
Rearrange:
(1+k)zq+1+(1−k)λ=2zq+1
Factorize:
(1+k−2)zq+1=−(1−k)λ
Attracting Fixed Point: If ∣1+k∣>2, infinity becomes an attracting fixed point.
That’s how we can write:
|R(z)|>|z|for|z|>M
where M is a threshold beyond which iterates escape to infinity. Using bounds, the escape criterion simplifies to:
|R(z)|=|(1+k)zq+1+(1−k)λ2zq|>|z|
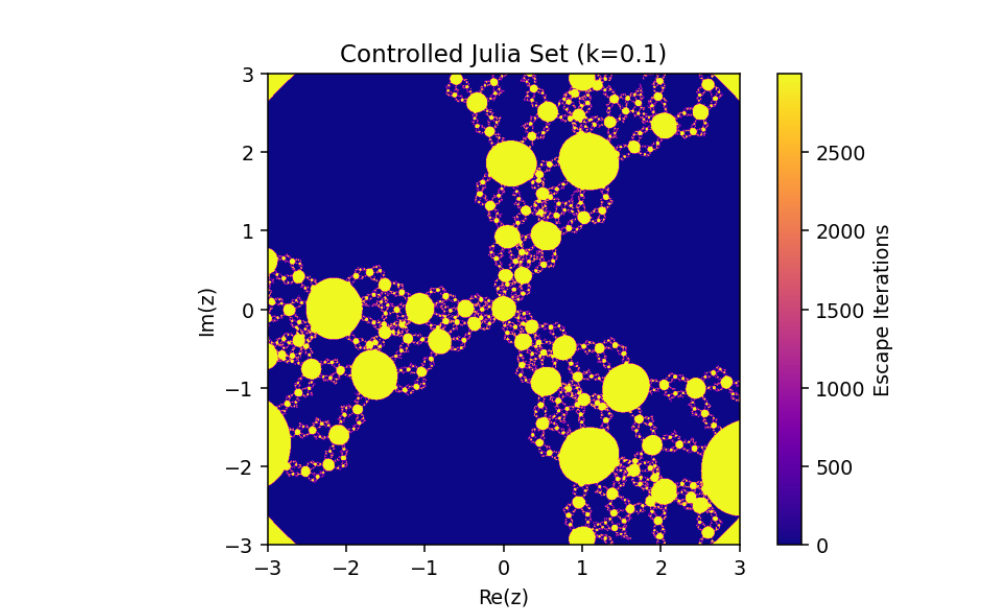
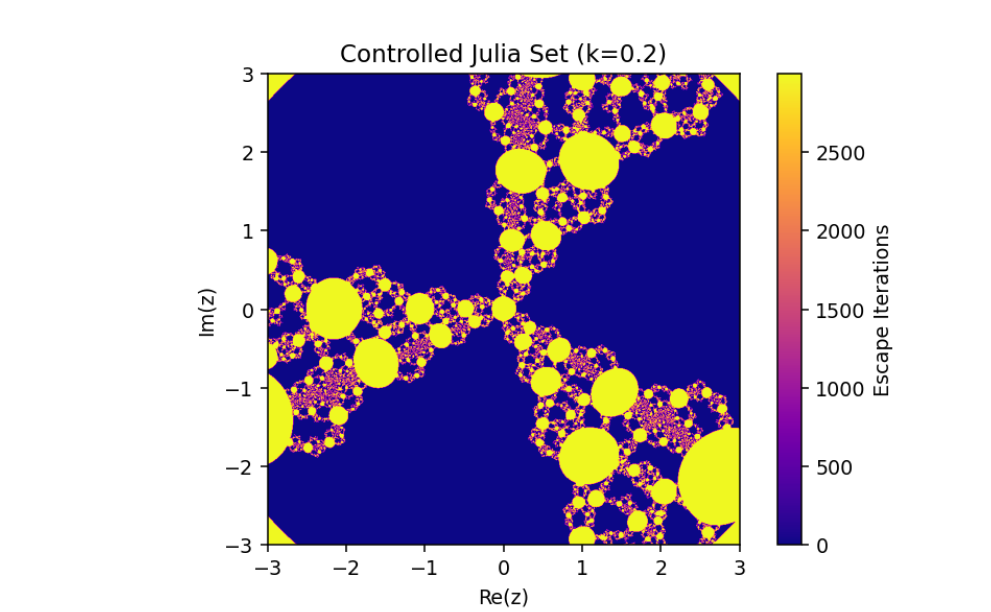
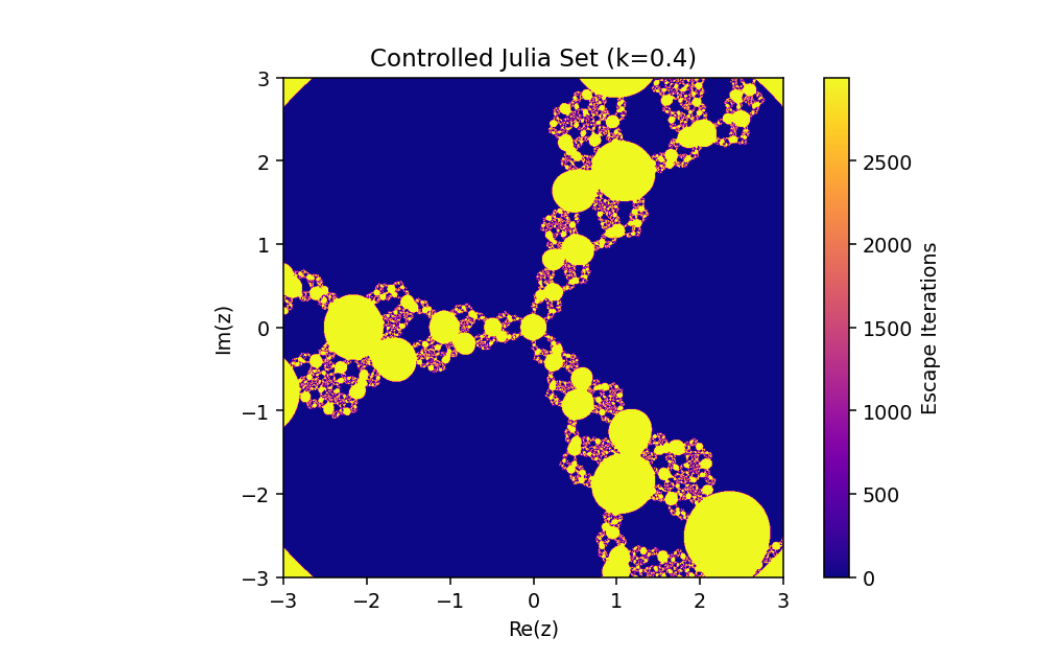
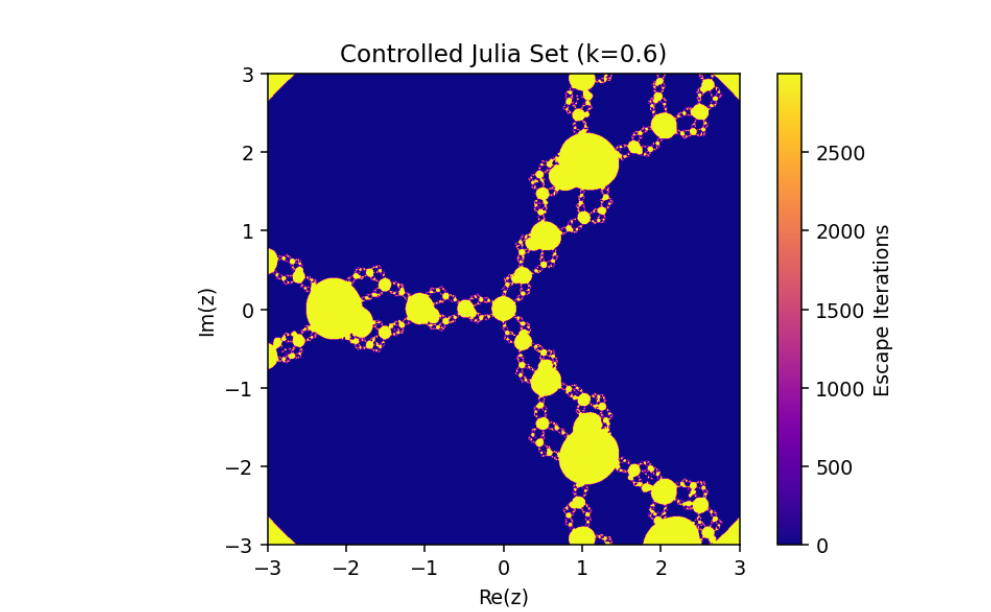
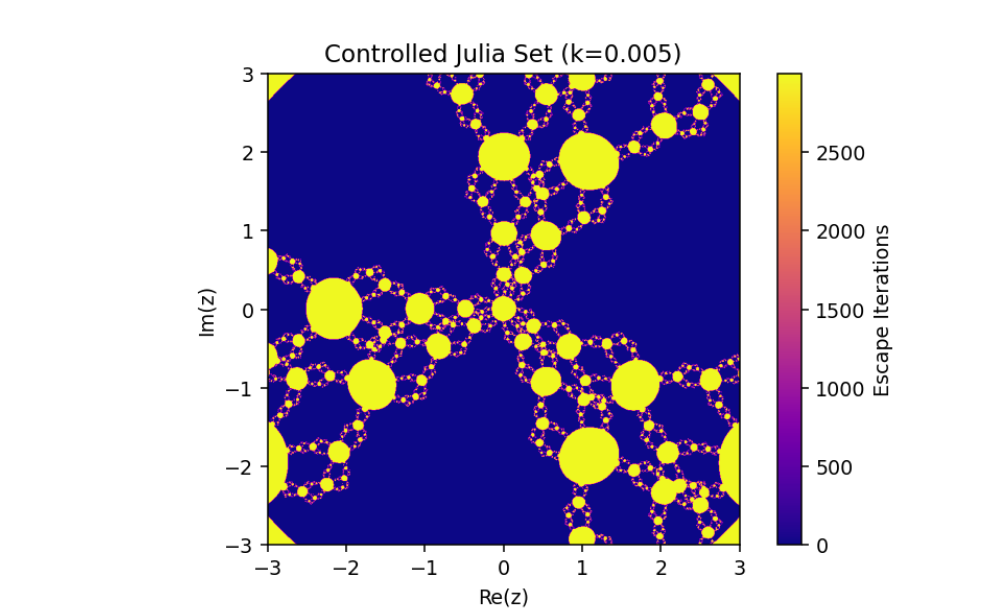
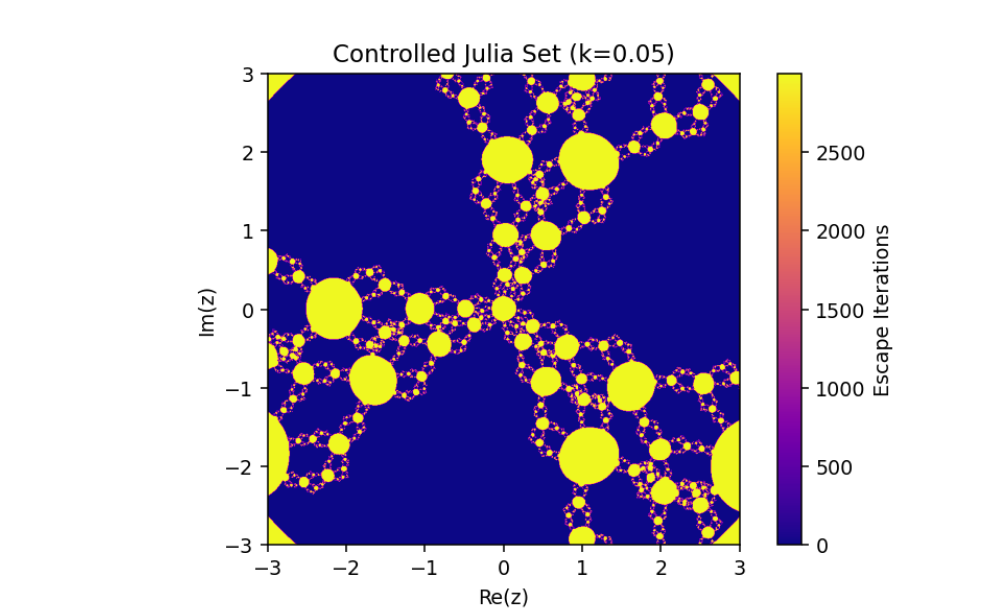
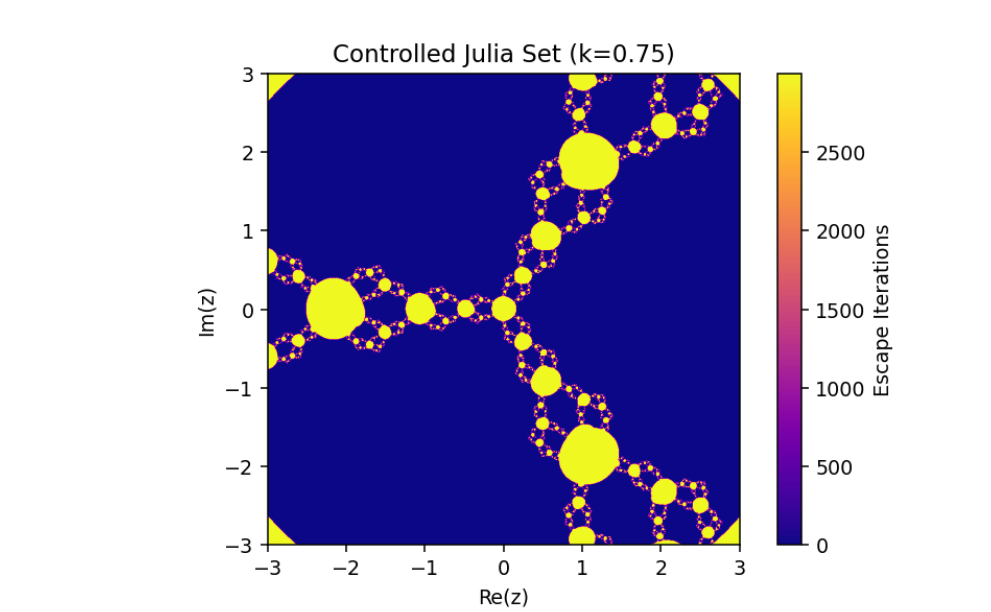
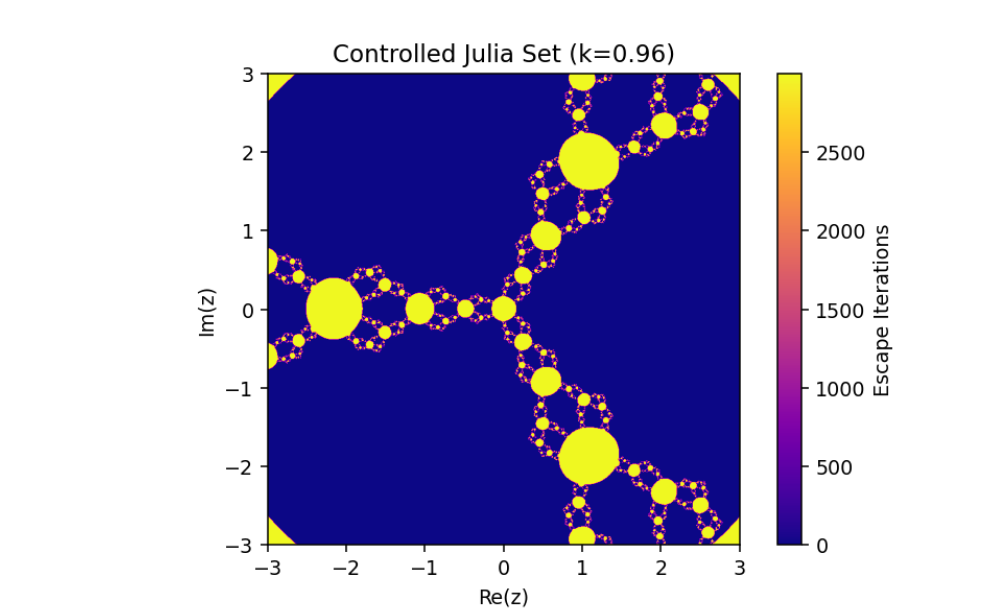
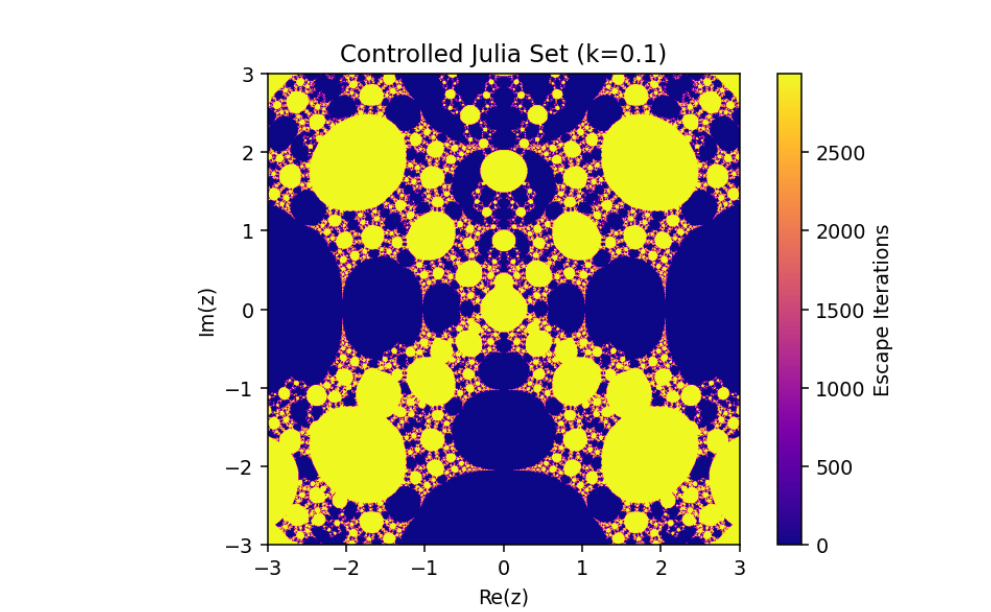
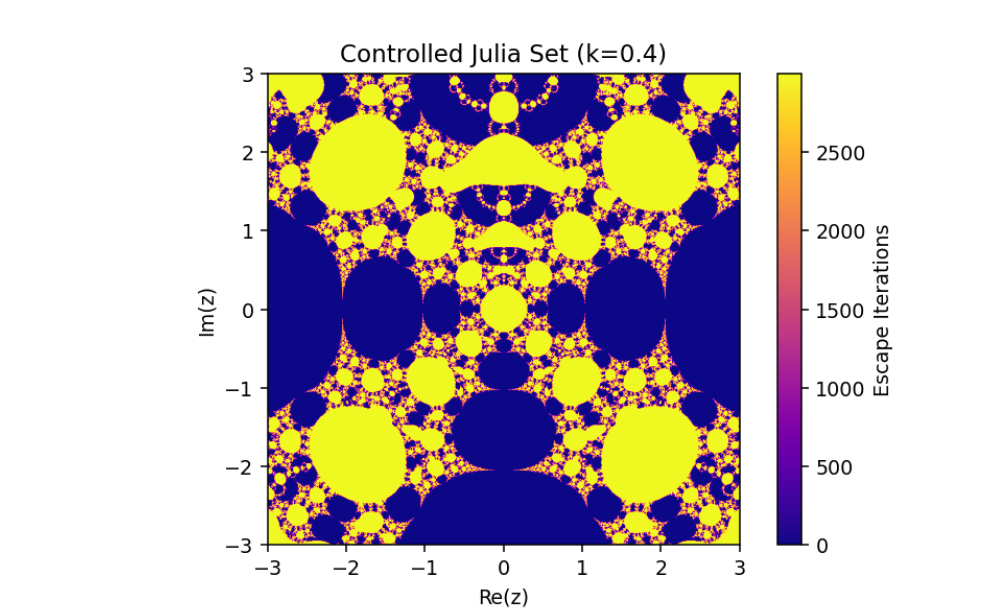
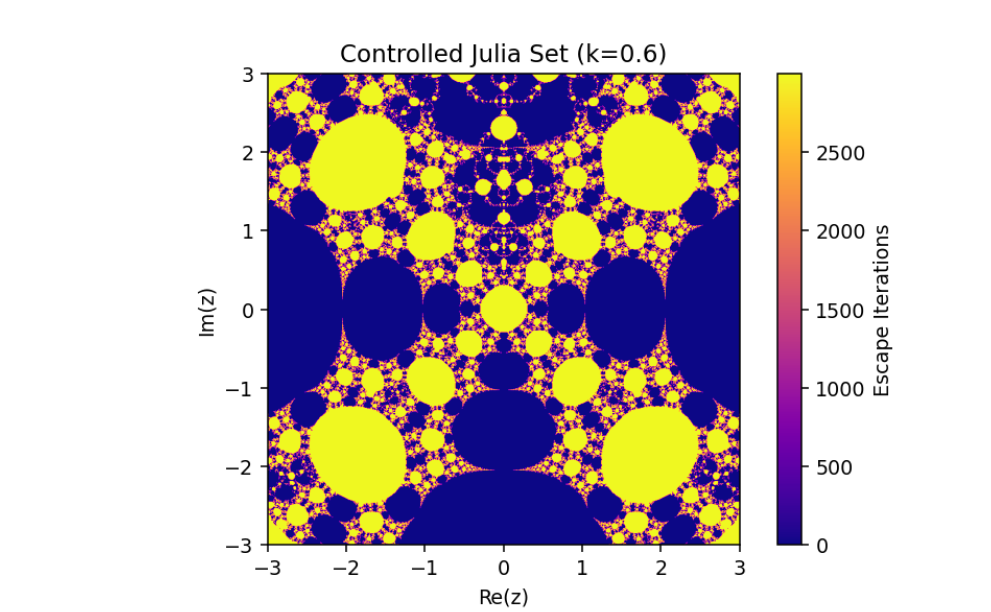
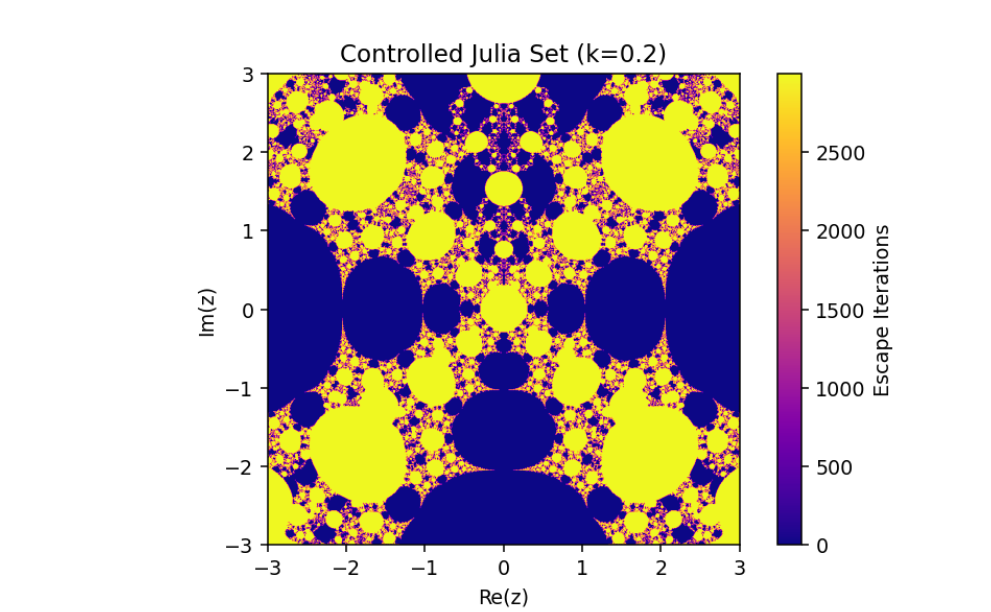
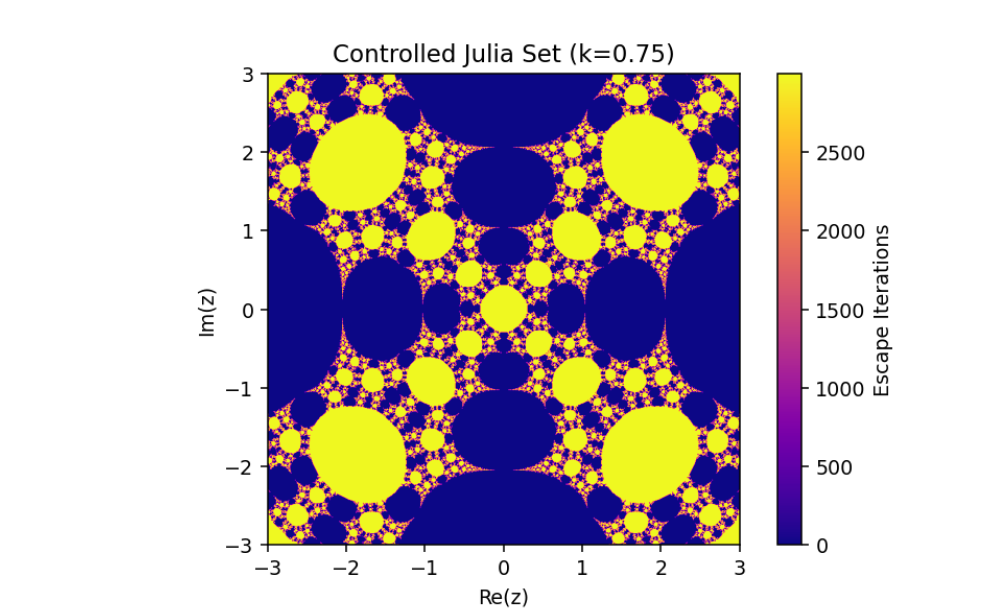
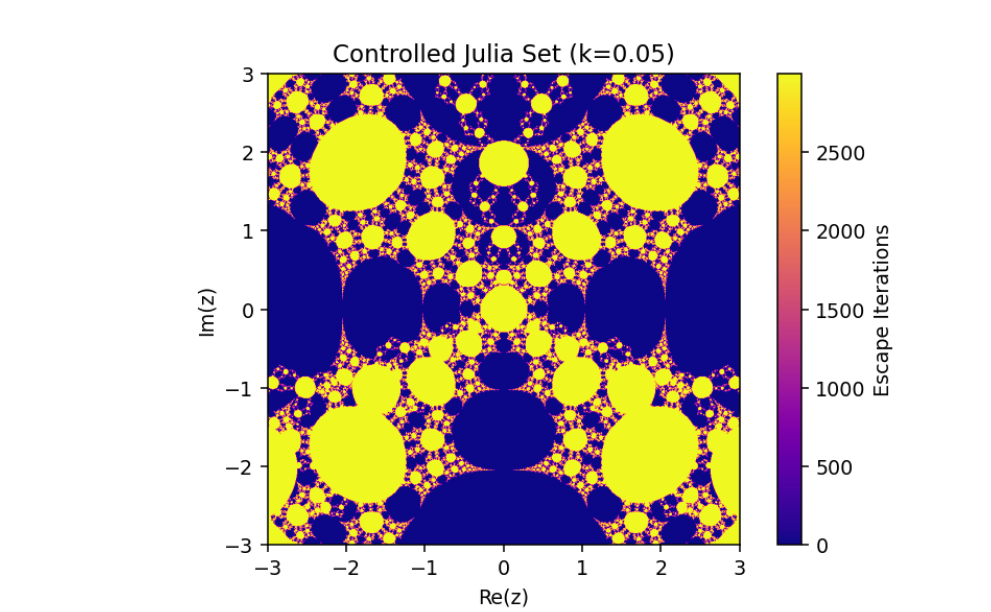
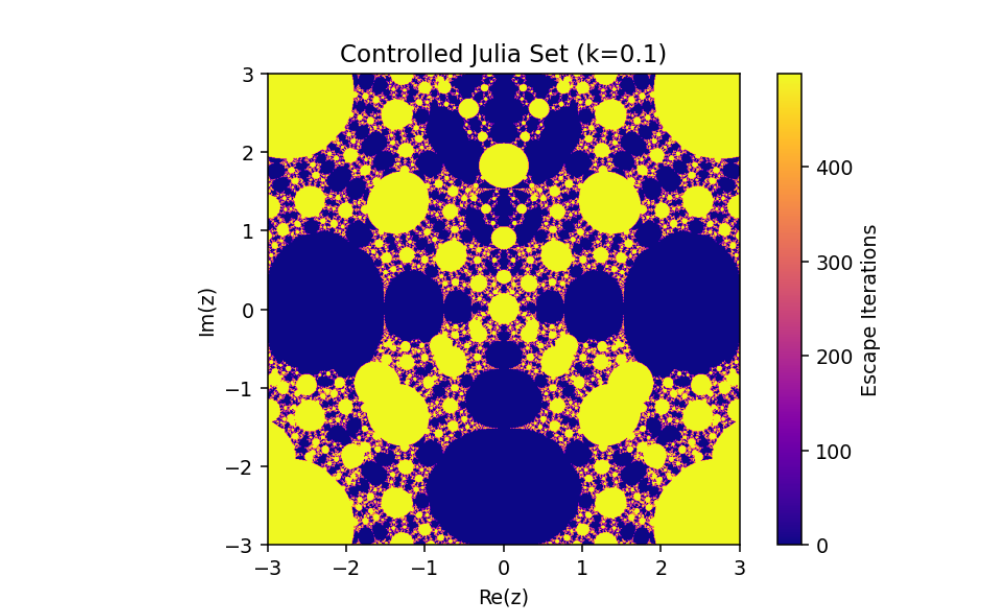
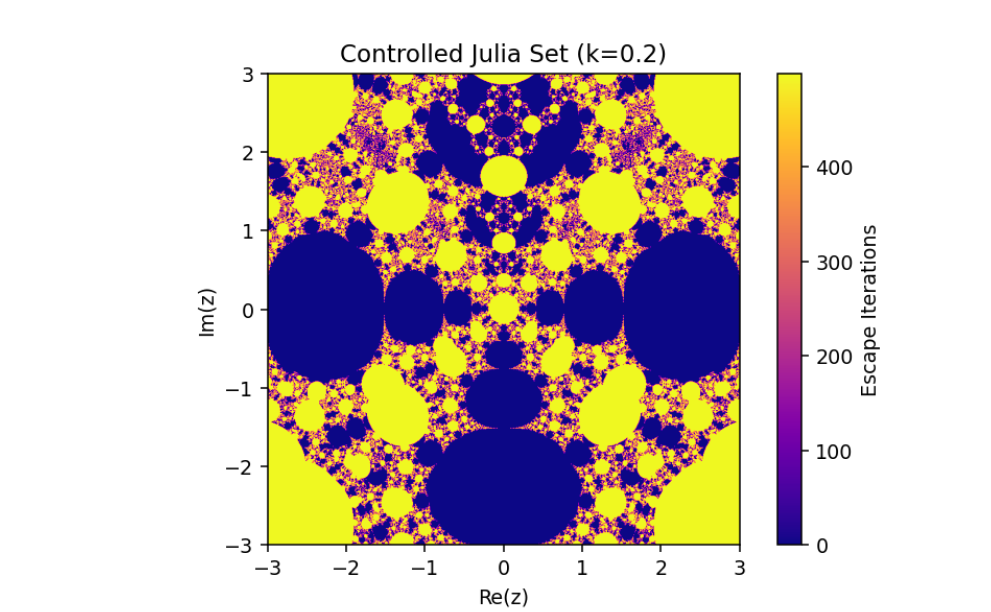
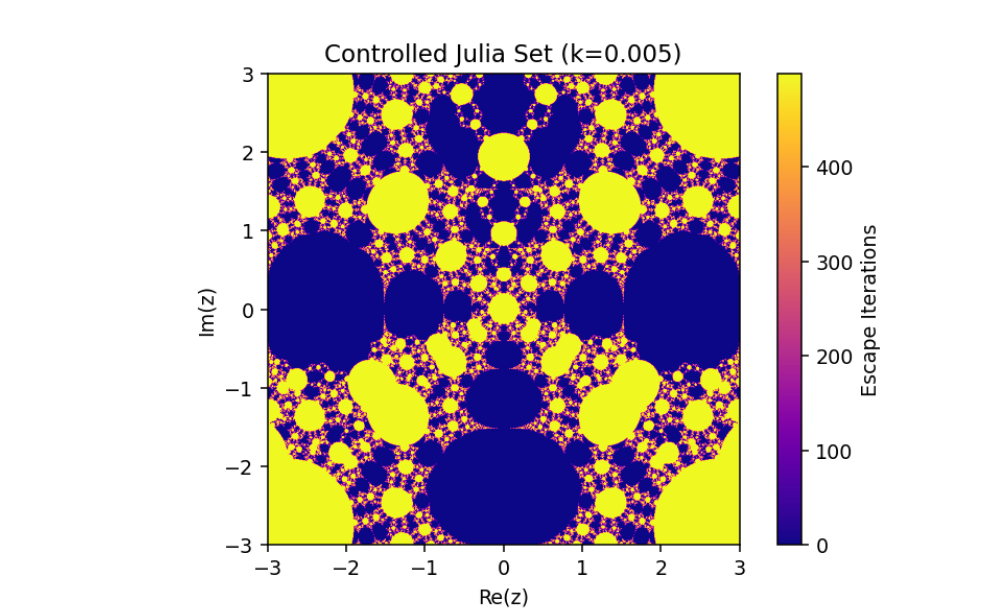
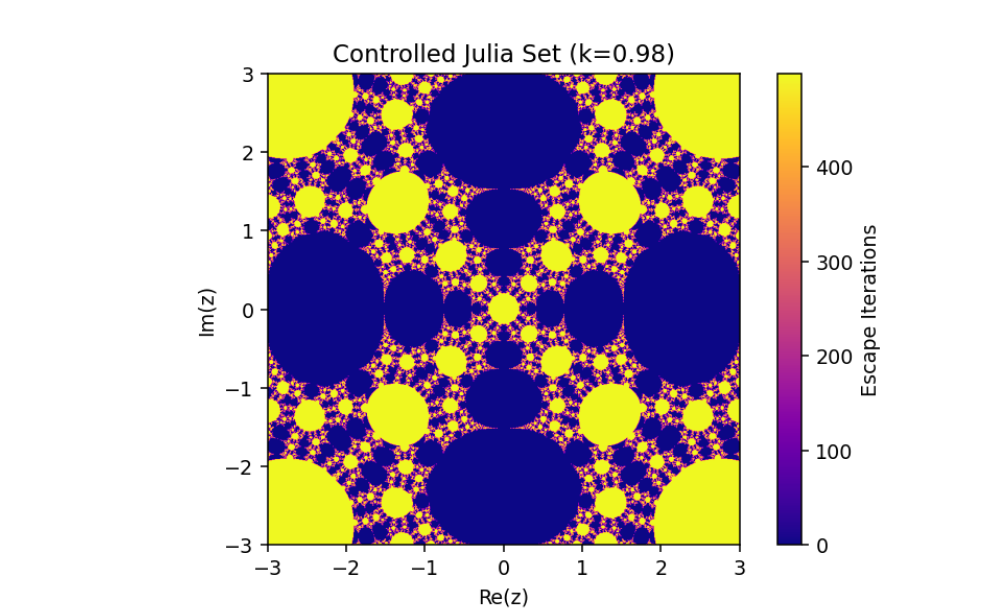
The control parameter k influences the structure of the Julia set.
As ∣1+k∣>2, infinity becomes an attracting fixed point, shrinking the Julia set.
The escape criterion ensures iterates either escape to infinity or remain bounded within the Julia set boundary.
Optimal Control Function
The control function modifies the system to regulate its fractal properties. For the perturbed rational map: zn+1=R(zn)+un,un+1=−k[R(zn+1)−R(zn)]+tun, where un introduces feedback to stabilize desired behaviors.
Key results include:
With t=k, the controlled system simplifies to: zn+1=R(zn)−k[R(zn)−zn].
This introduces a parameter k that governs the structure and behavior of the Julia set.
Iterative Function:
zn+1=zqn+c+λzpnwhere:
p,q∈Z+, are positive integers.
λ,c∈C are complex parameters.
zn∈C is the iterated sequence.
Boundedness Criterion:
A point z0 in the complex plane belongs to the filled Julia set if its orbit {z0,z1,z2,…} remains bounded under iteration.
For practical purposes, we compute boundedness using an escape radius R:
If |zn|>R, the point escapes to infinity.
Otherwise, it is bounded.
Key Parameters:
q: Controls the growth of the polynomial term.
λ: Perturbation parameter that introduces singularities at the origin.
p: Governs the strength of the singularity.
c: Determines the central point of the hyperbolic component in the Mandelbrot set.
Mathematical Framework for Visualization
The study relies on the escape-time algorithm to visualize Julia sets:
Initialize a grid of points in the complex plane.
Iterate each point under the map zn+1=R(zn).
Assign colors based on the number of iterations required to escape a bounded region.
This technique provides insights into the influence of control parameters k and synchronization mechanisms on the fractal structure.
Steps:
Initialize Grid:
- Define a grid of points in the complex plane z0, e.g., x,y∈[−2,2].
Iterative Mapping:
For each z0, compute its orbit:
zn+1=zqn+c+λzpn
Escape-Time Calculation:
Track the number of iterations n required for |zn| to exceed a given escape radius R.
Assign a colour to z0 based on n (e.g., gradient or palette).
Edge Cases:
Points where zn diverges rapidly (|zn|→∞) are coloured differently.
Points that remain bounded ( |zn|≤R after the maximum iteration) are typically coloured black (belong to the Julia set).
Synchronization of Julia Sets of the Complex System
A Descriptive Approach Synchronization of Julia Sets
- Mathematical Settings
- Mathematical Interpretation
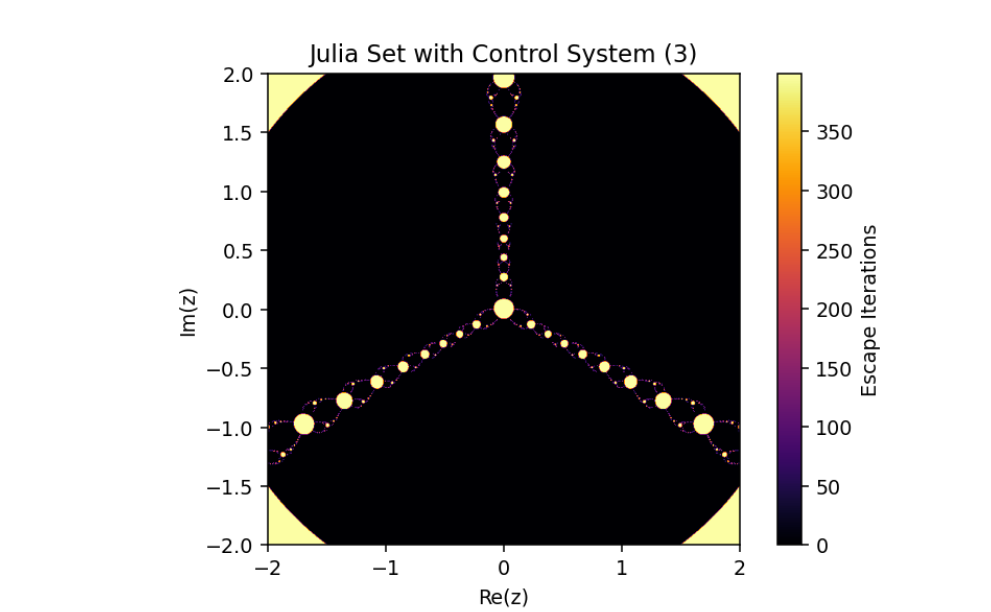
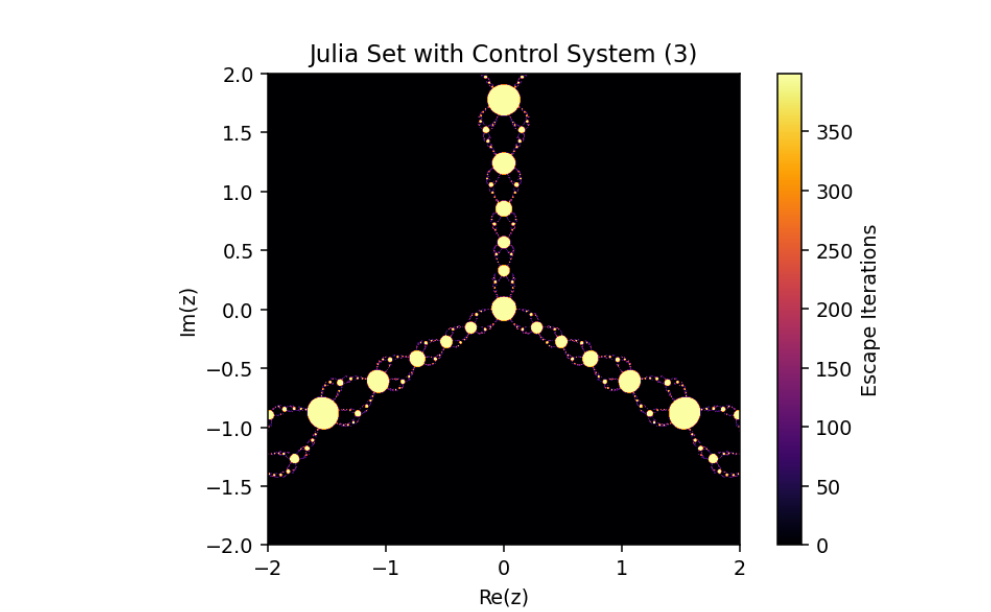
- Controlled System (5) when q=2,p=2,λ=0.073i
- Controlled System (5) when q=2,p=3,λ=0.073i,μ=0.1
- Controlled System (5) when q=2,p=3,λ=0.073i,μ=0.03
This phenomenon arises in the study of coupled systems, particularly in complex dynamics, where multiple Julia sets, associated with different parameters, exhibit coordinated behavior. Synchronization involves aligning the trajectories and fractal properties of two systems:
Driving System:
wn+1=12(wn+μwpn)with parametersp,μ....(4)
Response System:
zn+1=R(zn)−k[R(zn)−R(wn)]
Synchronization is achieved when the trajectory difference: |zn+1−wn+1|→0,ask→1.
Coupling Mechanism
The response system incorporates a coupling term to align its dynamics with the driving system:
wn+1=f(wn,λ1,q1)
zn+1=f(zn,λ2,q2)−k⋅(f(zn,λ2,q2)−f(wn,λ1,q1))
where k is a control parameter. The coupling ensures that the trajectory of zn (response) gradually approaches wn (driving). Over time, the Julia sets of the two systems synchronize, exhibiting identical or nearly identical fractal structures.
Why Synchronization Works
Synchronization is feasible because:
Both systems originate from the same functional framework.
Differences are limited to parameter variations (λ , q).
The coupling mechanism effectively bridges the gap created by these parameter differences, aligning the trajectories and fractal properties.
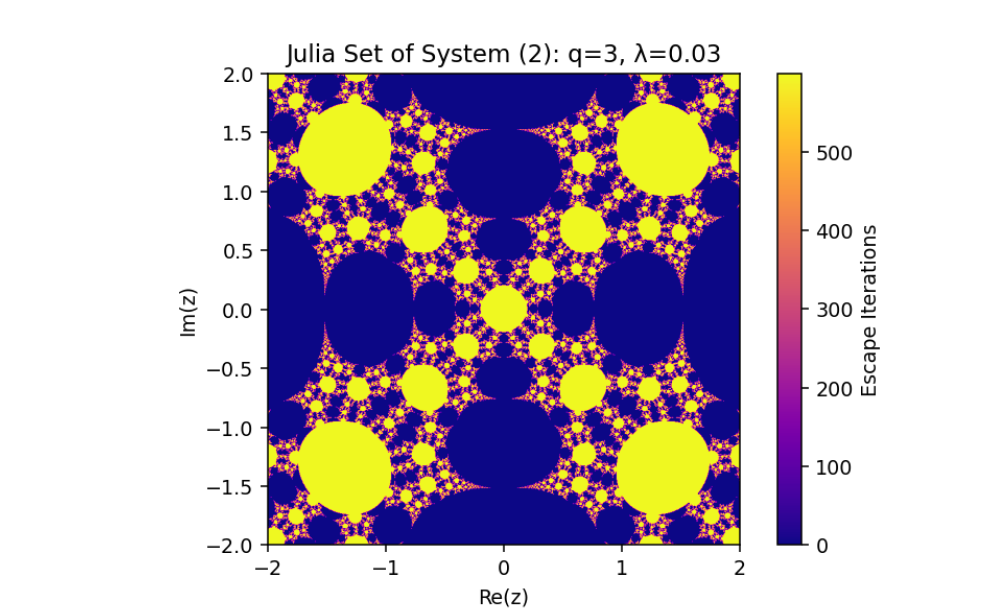

The equation provided is:
zn+1=12(zn+λzqn)−k[12(zn+λzqn)−12(wn+μwpn)]...(5)
where:
zn: Represents the primary iterated complex variable.
wn: Represents a secondary complex variable interacting with zn.
λ: A complex parameter controlling the rational map dynamics.
μ: Another complex parameter that modifies the wn dependent term.
p,q: Positive integers controlling the degree of the respective rational maps.
k: A feedback control parameter.
a modified version of a Julia set generated by introducing a control mechanism into the dynamics of a rational map.
This mechanism alters the behavior of the system, enabling adjustments to its fractal properties based on a coupling or control parameter k. Let’s break down this system and analyze its mathematical structure:
Base Map Contribution:
12(zn+λzqn)
forms the unperturbed Julia set, as seen in System (2).
Secondary Influence:
12(wn+μwpn)
introduces a coupling between the zn and wn dynamics, with the parameter μ adjusting this interaction.
Control Mechanism: The term:
−k[12(zn+λzqn)−12(wn+μwpn)]
applies feedback that synchronizes the zn and wn based maps, creating a controlled fractal structure. The control parameter k determines the extent of this feedback.
This system describes a coupled rational map with feedback control, where:
Coupling: The term involving wn and μ/wpn introduces a synchronized perturbation to the primary Julia set, ensuring dynamic interactions between zn and wn.
Feedback: The parameter k acts as a regulator, controlling the influence of the coupling term and modifying the convergence or divergence of points in the fractal.
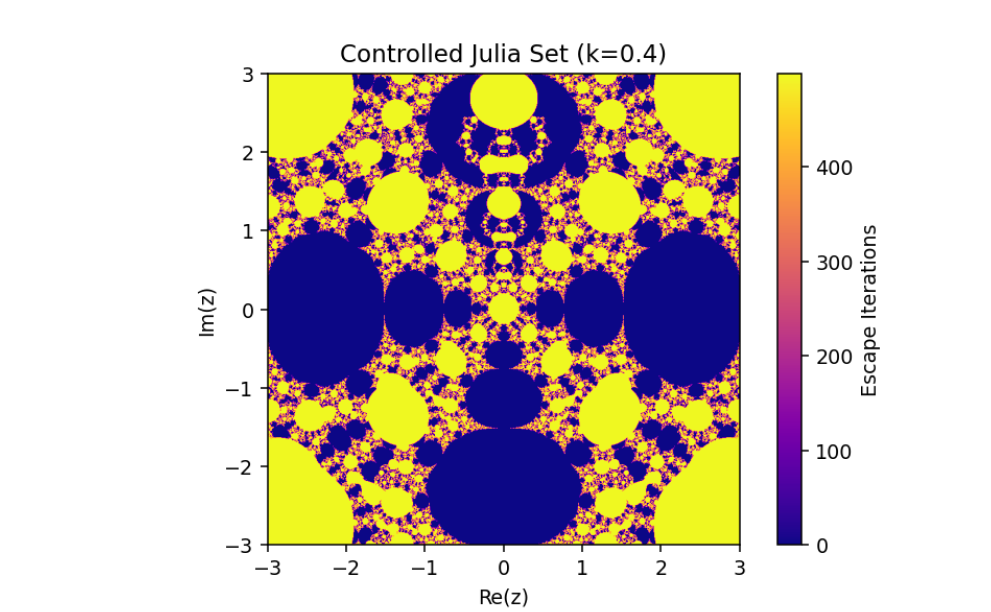
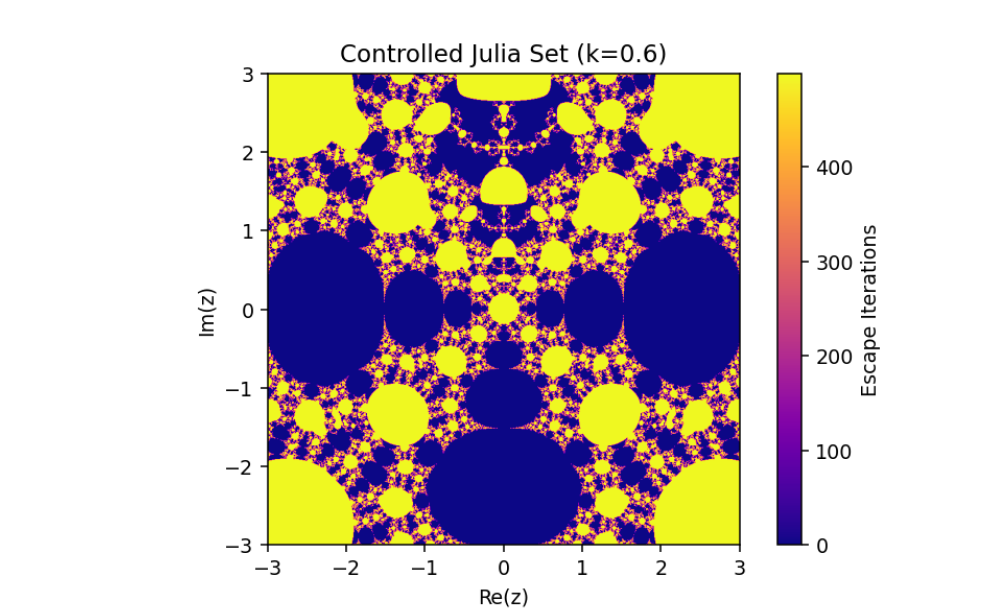
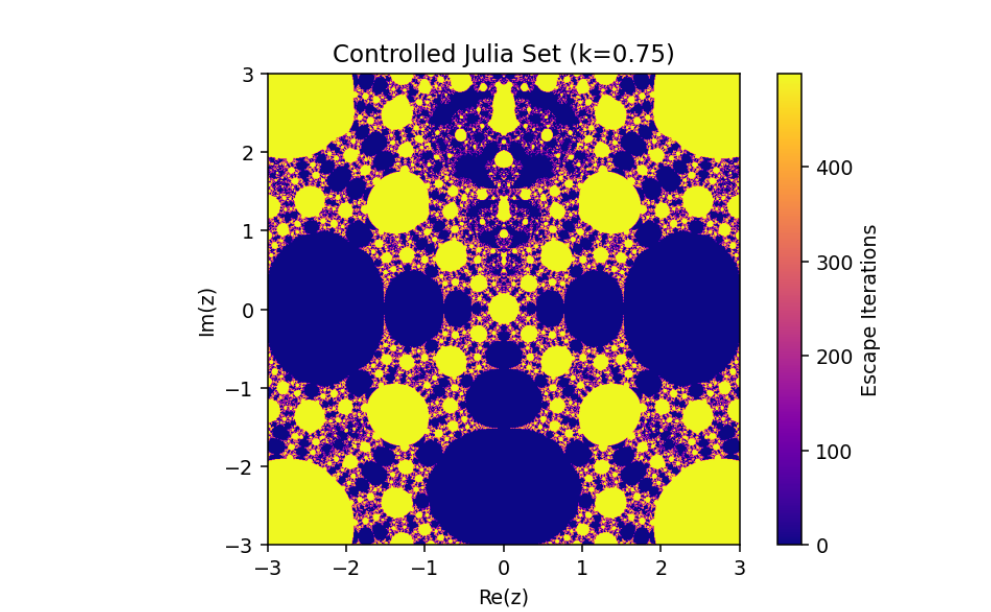
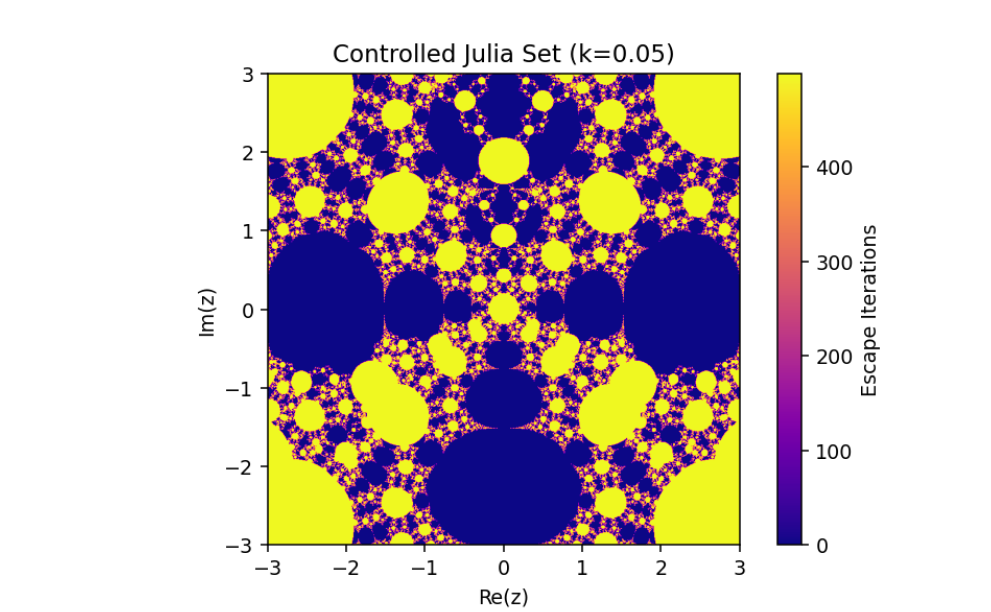
Conclusion
In this paper, we have discussed the control and synchronization of Julia sets of the complex perturbed rational maps zn+1=12(zn+λzqn), where infinity is regarded as a fixed point to be controlled. In many control methods, the fixed point of the system is finite. However, the fixed point of the complex perturbed rational maps is infinity. In order to avoid the unlimitedness of the fixed point, we take the optimal control function method to control the Julia sets of the complex perturbed rational maps since the fixed point could not appear in the control item. Through the control of Julia sets, we have that Julia sets of the perturbed rational maps are shrinking with the increasing control parameter k. By taking an item in the optimal control function to be the driving item, the synchronization of Julia sets with different system parameters in the perturbed rational maps is also studied. This idea provides a method to discuss the relation and changing of two different Julia sets but not a single one and we can make one Julia set change to be another.
References
Amritkar, R. E. & Gupte, N. [1993] “Synchronization of chaotic orbits: The effect of a finite time step,” Phys. Rev. E 47, 3889–3895.
Carleson, L. C. & Gamelin, T. W. [1993] Complex Dynamics (Springer-Verlag, NY).
Beck, C. [1999] “Physical meaning for Mandelbrot and Julia sets,” Physica D 125, 171–182.
Zhang, Y. & Sun, W. [2011] “Synchronization and coupling of Mandelbrot sets,” Nonlin. Dyn. 64, 59–63.
Zhang, Y., Sun, W. & Liu, C. [2010] “Control and synchronization of second Julia sets,” Chin. Phys. B 19, 050512.
Kocarev, L. & Parlitz, U. [1996] “Synchronizing spatiotemporal chaos in coupled nonlinear oscillators,” Phys. Rev. Lett. 77, 2206–2209.
Thank You

https://abhirup-moitra-mathstat.netlify.app/