Creating Dynamic Patterns with Complex Functions in R
Persuing M.Sc.Mathematics with Data Science, Institute of Mathematics & Application, Bhubaneswar, Odisha
Why do We Study Dynamic Patterns?
Why Do We Study Patterns?
Studying patterns is a fundamental aspect of understanding the world around us. Patterns provide insights into natural phenomena, human behavior, and even abstract mathematical concepts.
Understanding the Natural World
Predicting and Forecasting
Efficiency and Optimization
Human Behavior and Social Sciences
Art and Aesthetics
Mathematical Exploration
Problem Solving
Understanding Complex Systems
Biological and Medical Research
Reasons Behind Creating Dynamic Patterns
Visualizing Mathematical Concepts
Intersection of Art and Mathematics
Educational Value
Innovation and Creativity
Application of Technology
Exploring Symmetry and Chaos
The World is Full of Natural Visual Patterns
Harmonic Tapestry of Mathematics
The Enchanting World of the Harmonograph


Principles of Harmonic Motion
# Required Packages
install.packages("gganimate")
install.packages("magick")
# Load necessary libraries
library(tidyverse)
library(gganimate)
library(magick)
# Parameters for the pendulum
g <- 9.81 # acceleration due to gravity (m/s^2)
L <- 1 # length of the pendulum (m)
theta0 <- 0.2 # initial angle (in radians)
# Time sequence for the animation
time <- seq(0, 10, length.out = 500) # total time 10 seconds
# Function to calculate angular position over time
theta_t <- function(t) {
return(theta0 * cos(sqrt(g / L) * t))
}
# Data frame to store pendulum positions
pendulum_data <- data.frame(
time = time,
theta = theta_t(time),
x = L * sin(theta_t(time)),
y = -L * cos(theta_t(time))
)
# Plotting the pendulum
p <- ggplot(pendulum_data, aes(x = 0, y = 0)) +
geom_point(aes(x = x, y = y), color = "blue", size = 5) + # bob
geom_segment(aes(xend = x, yend = y), size = 1) + # string
geom_hline(yintercept = 0, linetype = "dashed") + # equilibrium line
coord_fixed(ratio = 1) +
xlim(-L, L) +
ylim(-L, 0) +
labs(title = "Simple Pendulum Animation", x = "", y = "") +
theme_minimal() +
transition_reveal(time)
# Save the animation
anim <- animate(p, nframes = 100, fps = 10, width = 500, height = 500)
anim_save("simple_pendulum.gif", anim)
From Pendulum Swings to Digital Brushstrokes
f1=jitter(sample(c(2,3),1))
f2=jitter(sample(c(2,3),1))
f3=jitter(sample(c(2,3),1))
f4=jitter(sample(c(2,3),1))
d1=runif(1,0,1e-02)
d2=runif(1,0,1e-02)
d3=runif(1,0,1e-02)
d4=runif(1,0,1e-02)
p1=runif(1,0,pi)
p2=runif(1,0,pi)
p3=runif(1,0,pi)
p4=runif(1,0,pi)
xt = function(t) exp(-d1*t)*sin(t*f1+p1)+exp(-d2*t)*sin(t*f2+p2)
yt = function(t) exp(-d3*t)*sin(t*f3+p3)+exp(-d4*t)*sin(t*f4+p4)
t=seq(1, 100, by=.001)
dat=data.frame(t=t, x=xt(t), y=yt(t))
with(dat, plot(x,y,
type="l",
xlim =c(-2,2),
ylim =c(-2,2),
xlab = "",
ylab = "",
xaxt='n',
yaxt='n'))
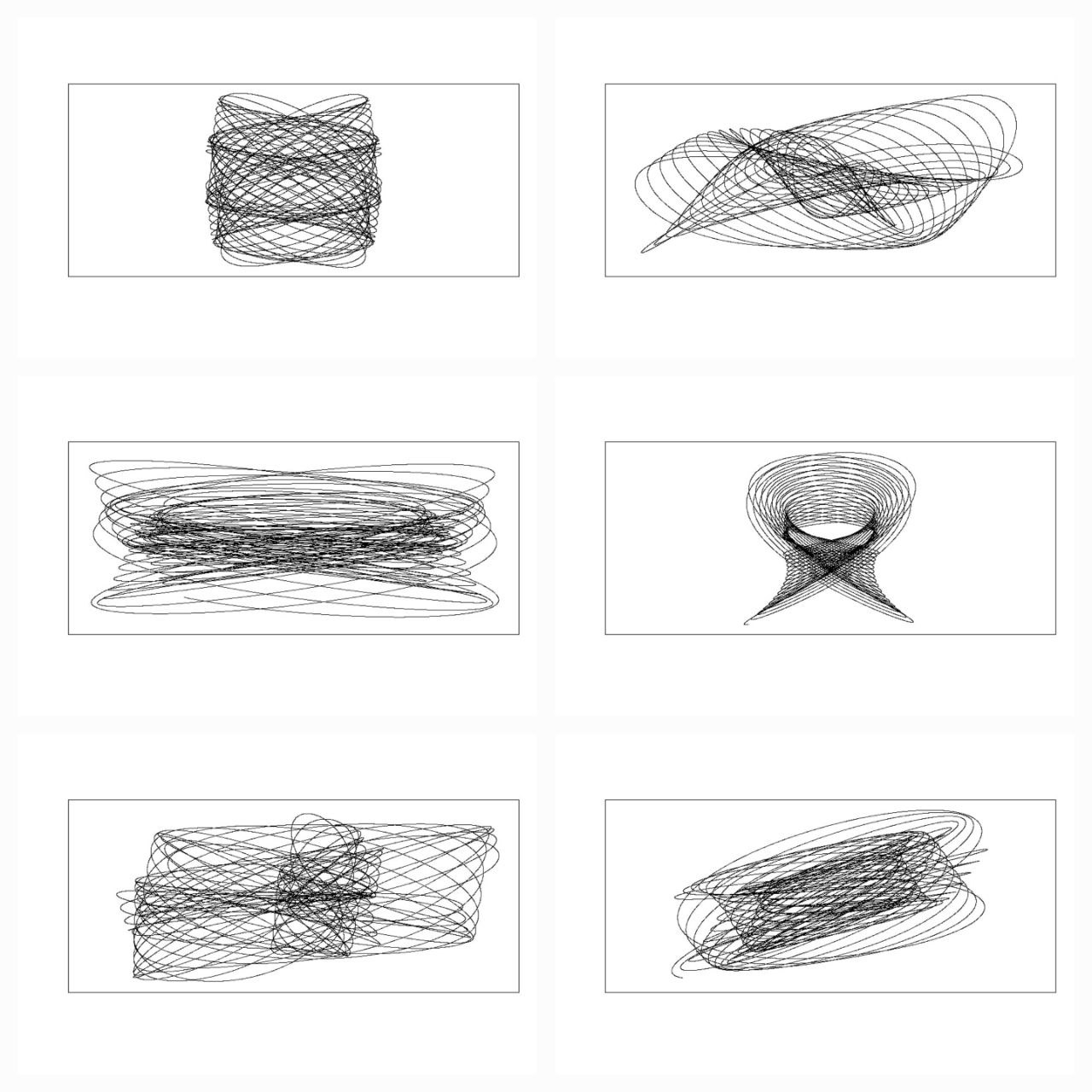
library(rgl)
library(scatterplot3d)
#Extending the harmonograph into 3d
#Antonio's functions creating the oscillations
xt = function(t) exp(-d1*t)*sin(t*f1+p1)+exp(-d2*t)*sin(t*f2+p2)
yt = function(t) exp(-d3*t)*sin(t*f3+p3)+exp(-d4*t)*sin(t*f4+p4)
#Plus one more
zt = function(t) exp(-d5*t)*sin(t*f5+p5)+exp(-d6*t)*sin(t*f6+p6)
#Sequence to plot over
t=seq(1, 100, by=.001)
#generate some random inputs
f1=jitter(sample(c(2,3),1))
f2=jitter(sample(c(2,3),1))
f3=jitter(sample(c(2,3),1))
f4=jitter(sample(c(2,3),1))
f5=jitter(sample(c(2,3),1))
f6=jitter(sample(c(2,3),1))
d1=runif(1,0,1e-02)
d2=runif(1,0,1e-02)
d3=runif(1,0,1e-02)
d4=runif(1,0,1e-02)
d5=runif(1,0,1e-02)
d6=runif(1,0,1e-02)
p1=runif(1,0,pi)
p2=runif(1,0,pi)
p3=runif(1,0,pi)
p4=runif(1,0,pi)
p5=runif(1,0,pi)
p6=runif(1,0,pi)
#and turn them into oscillations
x = xt(t)
y = yt(t)
z = zt(t)
#create values for colours normalised and related to x,y,z coordinates
cr = abs(z)/max(abs(z))
cg = abs(x)/max(abs(x))
cb = abs(y)/max(abs(y))
dat=data.frame(t, x, y, z, cr, cg ,cb)
#plot the black and white version
with(dat, scatterplot3d(x,y,z, pch=16,cex.symbols=0.25, axis=FALSE ))
with(dat, scatterplot3d(x,y,z, pch=16, color=rgb(cr,cg,cb),cex.symbols=0.25, axis=FALSE ))
#Set the stage for 3d plots
# clear scene:
clear3d("all")
# white background
bg3d(color="white")
#lights...camera...
light3d()
#action
# draw shperes in an rgl window
#spheres3d(x, y, z, radius=0.025, color=rgb(cr,cg,cb))
#create animated gif (call to ImageMagic is automatic)
#movie3d( spin3d(axis=c(0,0,1),rpm=5),fps=12, duration=12 )
#2d plots to give plan and elevation shots
plot(x,y,col=rgb(cr,cg,cb),cex=.05)
plot(y,z,col=rgb(cr,cg,cb),cex=.05)
plot(x,z,col=rgb(cr,cg,cb),cex=.05)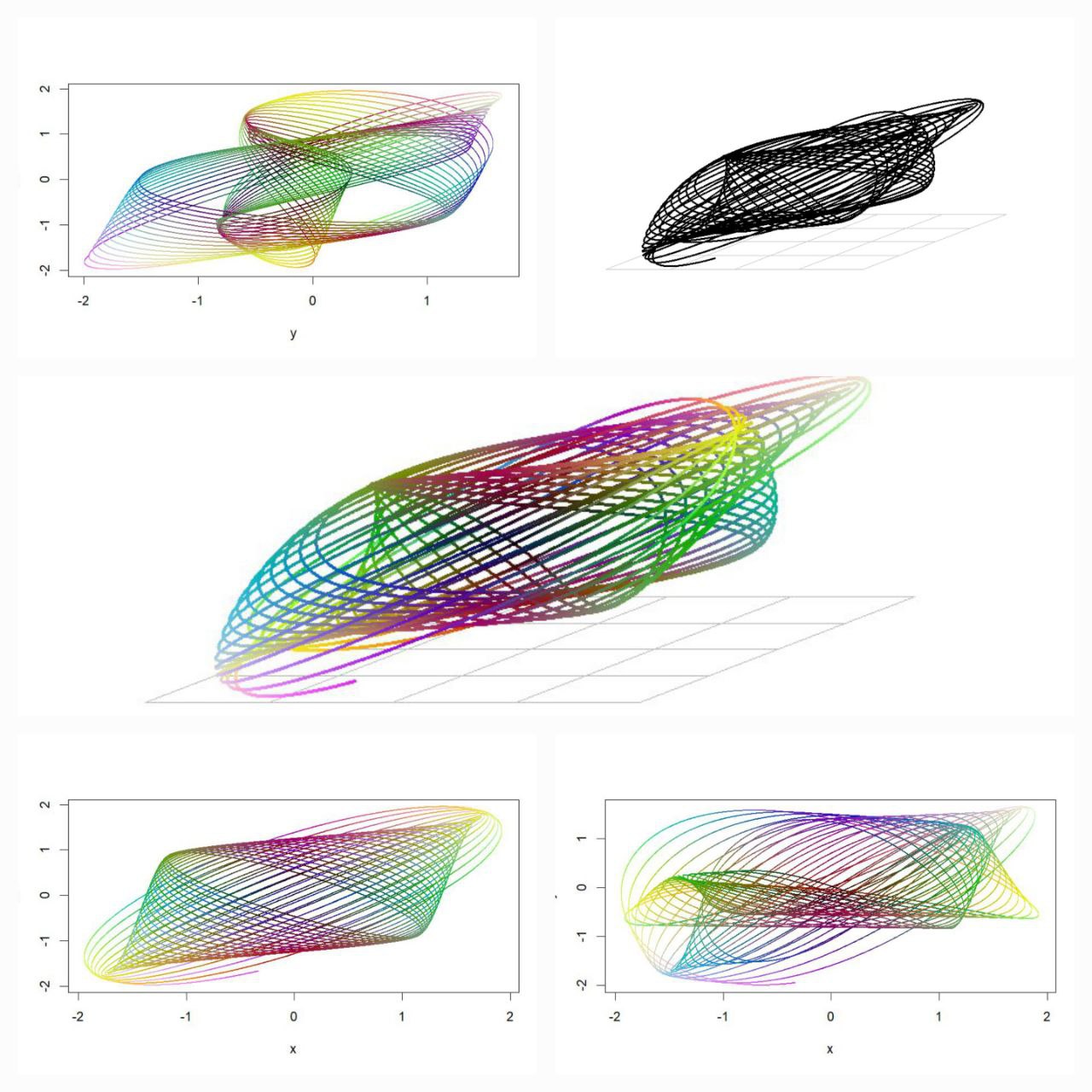
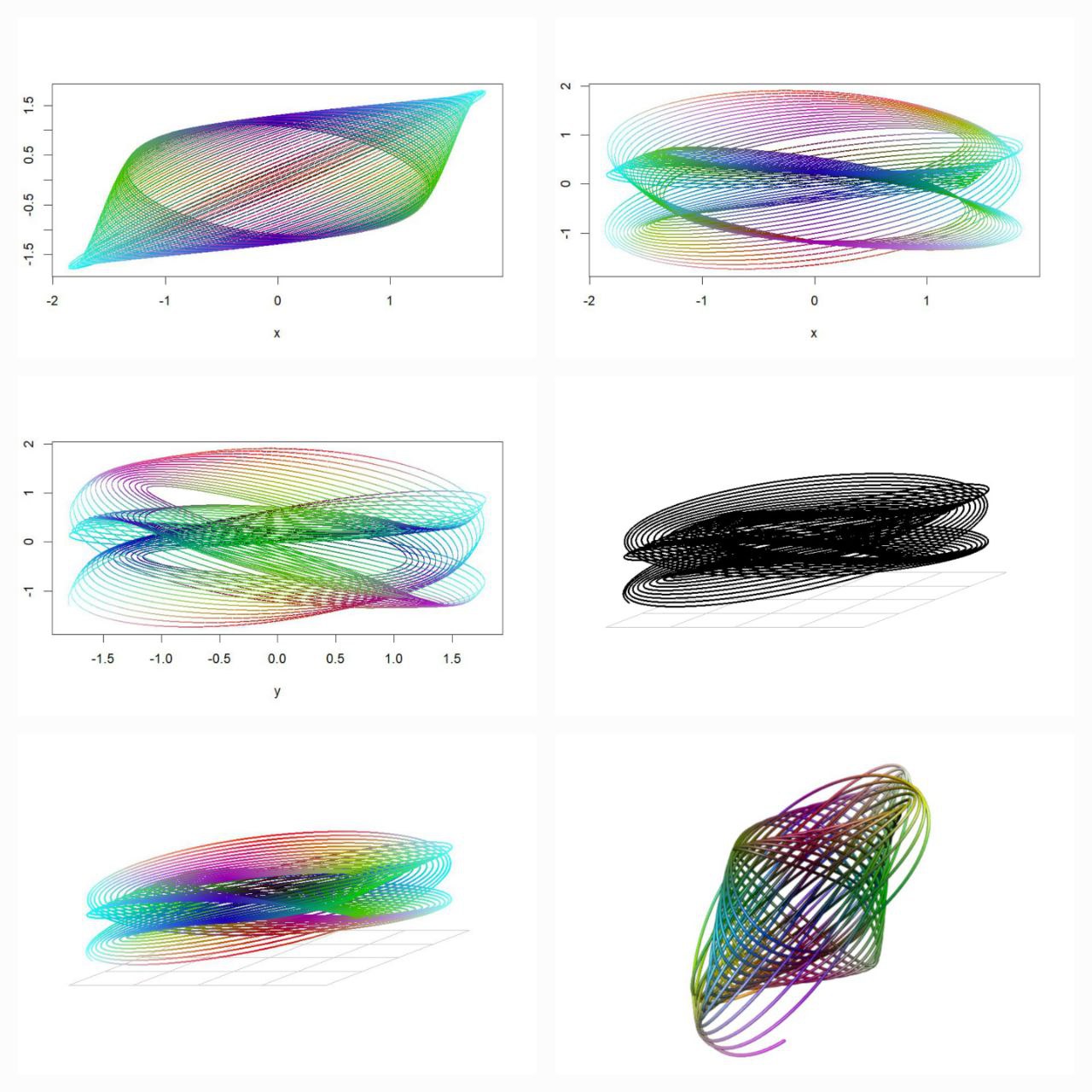
install.packages(c("devtools", "mapproj", "tidyverse", "ggforce", "Rcpp"))
devtools::install_github("marcusvolz/mathart")
library(devtools)
library(mathart)
library(ggforce)
library(Rcpp)
library(tidyverse)
df1 <- harmonograph(A1 = 1, A2 = 1, A3 = 1, A4 = 1,
d1 = 0.004, d2 = 0.0065, d3 = 0.008, d4 = 0.019,
f1 = 3.001, f2 = 2, f3 = 3, f4 = 2,
p1 = 0, p2 = 0, p3 = pi/2, p4 = 3*pi/2) %>% mutate(id = 1)
df2 <- harmonograph(A1 = 1, A2 = 1, A3 = 1, A4 = 1,
d1 = 0.0085, d2 = 0, d3 = 0.065, d4 = 0,
f1 = 2.01, f2 = 3, f3 = 3, f4 = 2,
p1 = 0, p2 = 7*pi/16, p3 = 0, p4 = 0) %>% mutate(id = 2)
df3 <- harmonograph(A1 = 1, A2 = 1, A3 = 1, A4 = 1,
d1 = 0.039, d2 = 0.006, d3 = 0, d4 = 0.0045,
f1 = 10, f2 = 3, f3 = 1, f4 = 2,
p1 = 0, p2 = 0, p3 = pi/2, p4 = 0) %>% mutate(id = 3)
df4 <- harmonograph(A1 = 1, A2 = 1, A3 = 1, A4 = 1,
d1 = 0.02, d2 = 0.0315, d3 = 0.02, d4 = 0.02,
f1 = 2, f2 = 6, f3 = 1.002, f4 = 3,
p1 = pi/16, p2 = 3*pi/2, p3 = 13*pi/16, p4 = pi) %>% mutate(id = 4)
df <- rbind(df1, df2, df3, df4)
p <- ggplot() +
geom_path(aes(x, y), df, alpha = 0.25, size = 0.5) +
coord_equal() +
facet_wrap(~id, nrow = 2) +
theme_blankcanvas(margin_cm = 0)
ggsave("harmonograph01.png", p, width = 20, height = 20, units = "cm")
From Pendulums to Patterns
Basic Formalism
Lissajous curves are the shapes traced out by sinusoidal motion in two dimensions. They are characterised by the equations:
\[ x = A \sin(f_xt - \delta_x) \]
\[ y = B \cos (f_yt - \delta_y) \]
where \(A\) and \(B\) are amplitudes, \(f_x\) and \(f_y\) are frequencies of the motion and \(\delta_x\) and \(\delta_y\) the phase shift.
Mathematical Harmony in Motion
library(ggplot2)
library(gganimate)
# Function to calculate position of simple harmonic oscillator
sho_position <- function(t, A, omega, phi) {
return(A * sin(omega * t + phi))
}
# Parameters
t <- seq(0, 2*pi, length.out = 100)
A1 <- 1 # Amplitude of oscillator 1
A2 <- 0.5 # Amplitude of oscillator 2
omega1 <- 1 # Angular frequency of oscillator 1
omega2 <- 1.5 # Angular frequency of oscillator 2
phi1 <- 0 # Phase of oscillator 1
phi2 <- pi/2 # Phase of oscillator 2
# Data for oscillator 1
df1 <- data.frame(t = t, position = sho_position(t, A1, omega1, phi1), oscillator = "Oscillator 1")
# Data for oscillator 2
df2 <- data.frame(t = t, position = sho_position(t, A2, omega2, phi2), oscillator = "Oscillator 2")
# Combine data
df <- rbind(df1, df2)
# Create plot
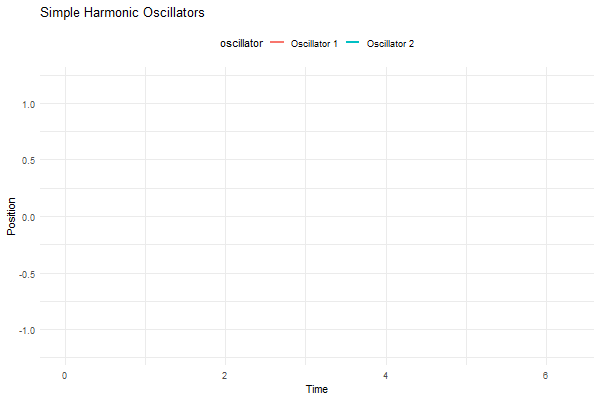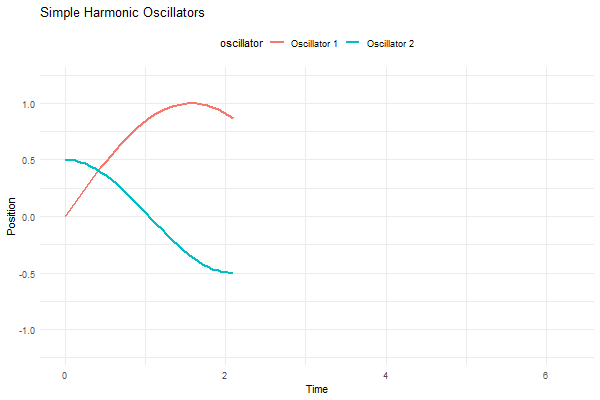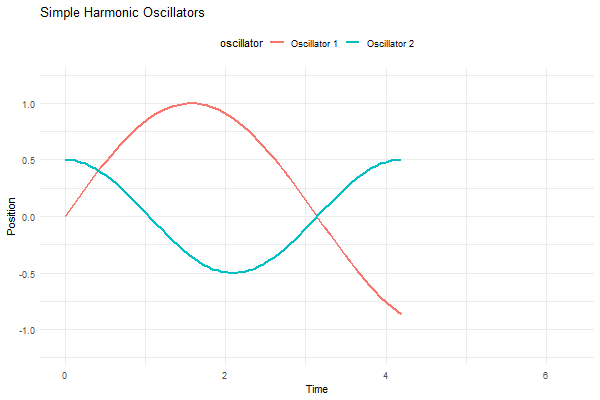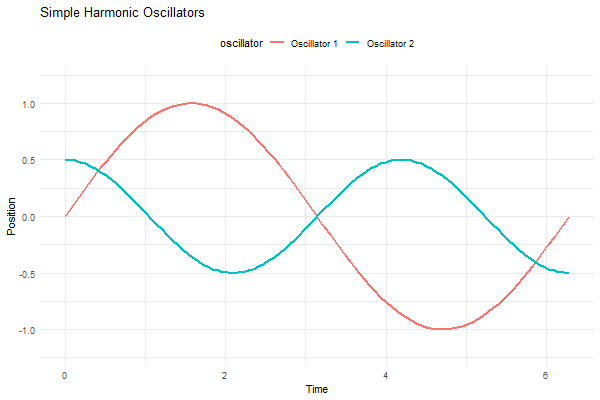
p <- ggplot(df, aes(x = t, y = position, group = oscillator, color = oscillator)) +
geom_line(size = 1) +
ylim(-1.2, 1.2) +
labs(title = "Simple Harmonic Oscillators", x = "Time", y = "Position") +
theme_minimal() +
theme(legend.position = "top") +
transition_reveal(t)
# Animate plot
animate(p, nframes = 100, duration = 10, width = 600, height = 400)
#___________________________________________________________________________
library(gifski)
# Function to calculate position of simple harmonic oscillator
sho_position <- function(t, A, omega, phi) {
return(A * sin(omega * t + phi))
}
# Parameters
t <- seq(0, 2, by = 0.01)
A <- 1 # Amplitude
omega1 <- 2*pi # Angular frequency of x-axis oscillator
omega2 <- 6*pi # Angular frequency of y-axis oscillator
limits <- c(-1, 1)
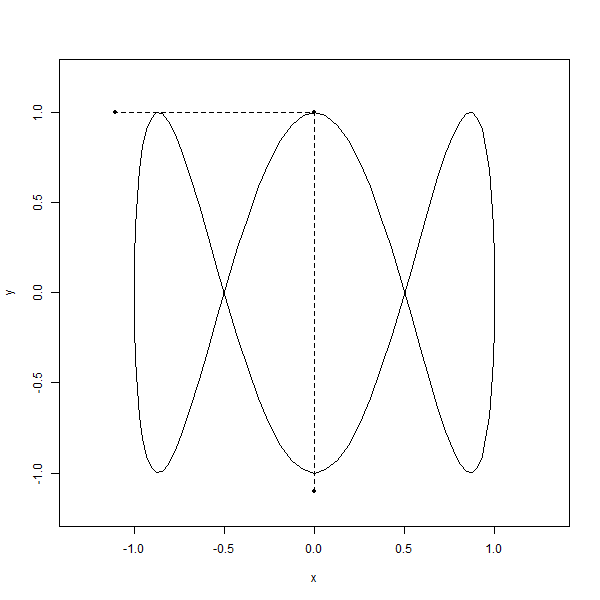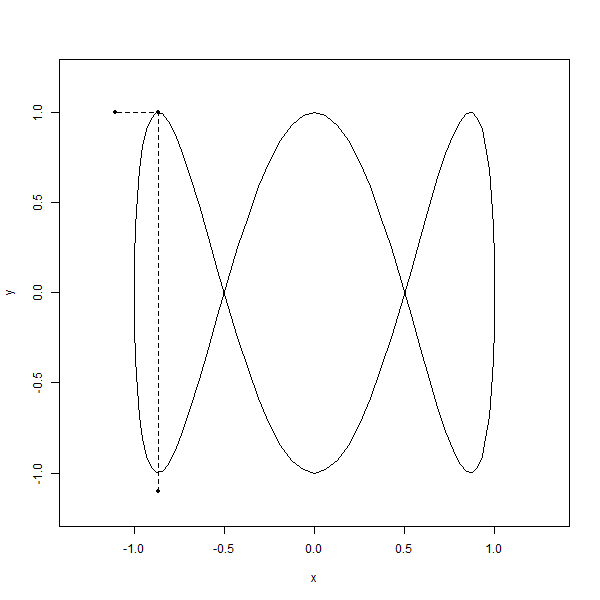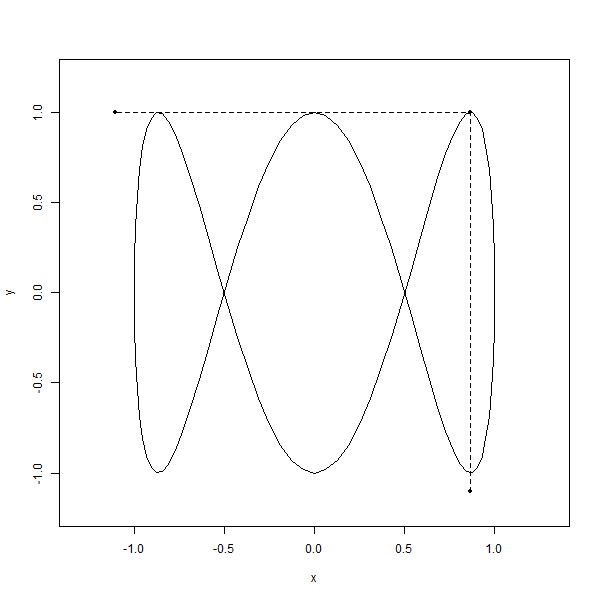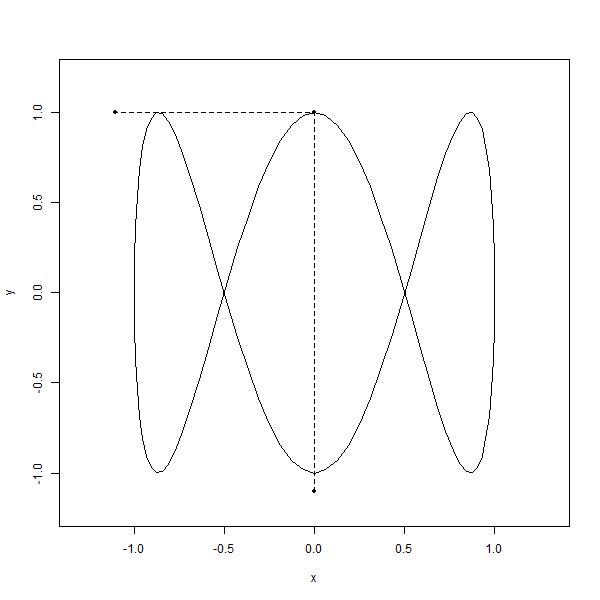
save_gif(
lapply(seq(0, 2, length.out = 100), function(i) {
x <- sin(2 * pi * t)
y <- cos(6 * pi * t)
plot(x, y, type = "l", asp = 1, xlim = 1.2 * limits, ylim = 1.2 * limits)
lines(x = c(sin(2 * i * pi), sin(2 * i * pi), -1.1),
y = c(-1.1, cos(6 * pi * i), cos(6 * pi * i)), pch = 20, type = "o", lty = "dashed")
}),
delay = 1 / 10, width = 600, height = 600, gif_file = "sho_animation.gif"
)
library(gifski)
# Parameters
t <- seq(0, 2, by = 0.01)
limits <- c(-1, 1)
save_gif(
lapply(1:10, function(i) {
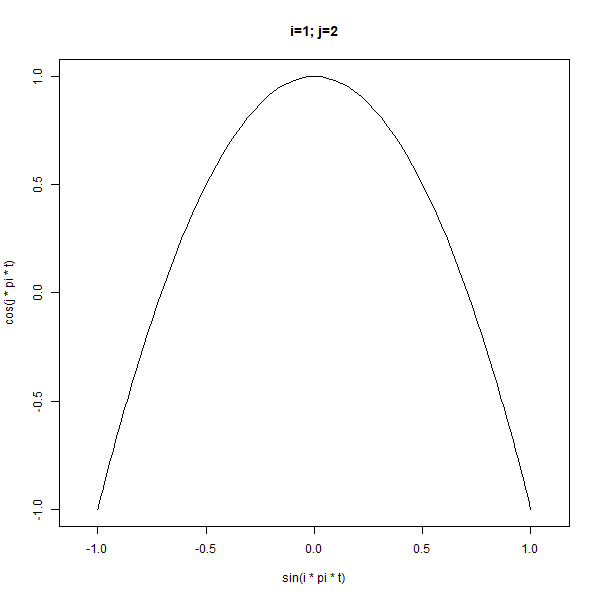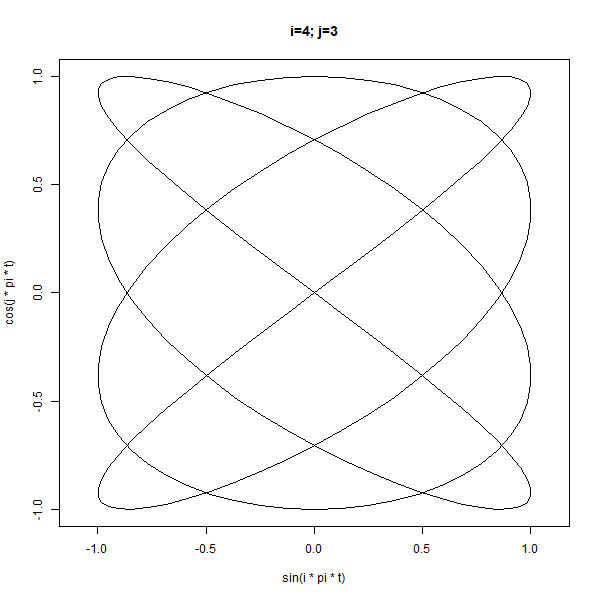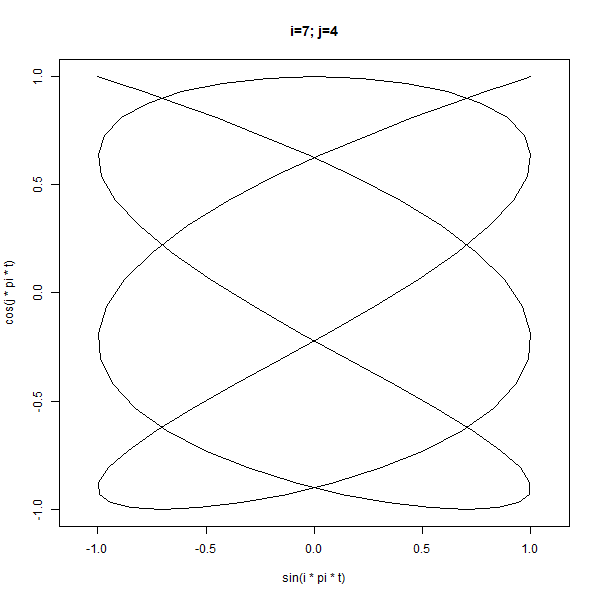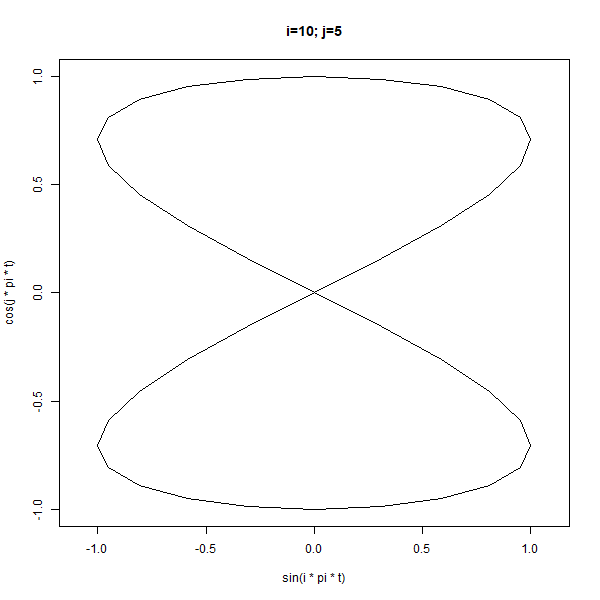
lapply(2:5, function(j) {
plot(x = sin(i * pi * t),
y = cos(j * pi * t),
type = "l", asp = 1, xlim = limits, ylim = limits,
main = sprintf("i=%d; j=%d", i, j))
})
}),
delay = 1/3, width = 600, height = 600, gif_file = "animation.gif"
)
A Visual Feast
Lissajous Curves
Lissajous curves unveils a world of mathematical beauty and scientific inquiry, inviting us to delve deeper into the intricate relationships between oscillatory systems. Whether as a tool for analysis, a source of artistic inspiration, or simply a captivating visual spectacle, the exploration of overlaid Lissajous curves promises endless fascination and discovery. Lissajous curves offer a plethora of intriguing possibilities beyond their initial creation. One fascinating avenue is the exploration of overlaying multiple curves with different frequencies, leading to a captivating array of patterns and forms.
Visual Tapestry
set.seed(2)
df <- lissajous(a = runif(1, 0, 2), b = runif(1, 0, 2), A = runif(1, 0, 2), B = runif(1, 0, 2), d = 200) %>%
sample_n(1001) %>%
k_nearest_neighbour_graph(40)
p <- ggplot() +
geom_segment(aes(x, y, xend = xend, yend = yend), df, size = 0.03) +
coord_equal() +
theme_blankcanvas(margin_cm = 0)
ggsave("knn_lissajous_002.png", p, width = 25, height = 25, units = "cm")
Mathematical Curves in Action
“Mathematics possesses not only truth but supreme beauty—a beauty cold and austere, like that of sculpture.” – Bertrand Russell

Recamán’s Sequence and R Graphics
Mathematics is replete with sequences that fascinate, challenge, and inspire. Among these is Recamán’s sequence, a non-traditional and intriguing sequence defined by a simple set of rules yet exhibiting complex and often surprising behaviour. Named after its creator, Colombian mathematician Bernardo Recamán Santos, this sequence offers a rich ground for exploration in number theory and recreational mathematics.
Definition and Construction
Recamán’s sequence \(\{a\}_{n\ge1}\) is defined as,
\[ \begin{equation} a_n= \begin{cases} 0, & \text{if } n=0\\ a_{n-1}-n, & \text{if } a_{n-1}-n >0\ \text{and is not already in the sequence} \\ a_{n-1}+n, & \text{otherwise } \end{cases}\end{equation} \]
This definition can be summarized in the form of an algorithm:
Initial step: \(a_0 = 0\)
Recursive step: For \(n>0:\)
If \(a_{n−1}−n>0\ \text{and}\) \(a_{n−1}−n\ \text{has not been used before, then}\) \(a_n=a_{n−1}−n\)
Otherwise, \(a_n=a_{n−1}+n\)
To better understand the construction, let’s compute the first few terms of Recamán’s sequence:
\(a_0 =0\)
\(a_1 = 0+1 =1\)
\(a_2 = 1-2 =-1\ \text{(not allowed since it is negative, so)}\ a_2 = 1+2=3\)
\(a_3 = 3-3 = 0\ \text{(already in the sequence,so)}\ a_3 =3+3 =6\)
\(a_4 = 6-4 =2\)
\(a_5 = 2-5 =-3\ \text{(not allowed since it is negative, so)}\ a_5 =2+5=7\)
\(a_6 = 7-6 = 1\text{(already in the sequence,so)}\ a_6 =7+6 =13\)
Continuing in this manner, the sequence begins as, \(0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10,\ldots\) This sequence is known for its interesting properties, such as the seemingly chaotic pattern of values and the fact that it often revisits the same values in different steps.
Properties and Patterns
Recamán’s sequence is known for its unpredictable and non-repetitive nature. Despite the straightforward rule governing its construction, the sequence does not follow a simple or easily discernible pattern. Some of its notable properties include:
Non-repetition: Each number in the sequence is unique, emphasizing the condition that no number should repeat.
Oscillatory behavior: The sequence oscillates, moving both forwards and backwards, but always progressing to larger values overall.
Density and Growth: The sequence grows indefinitely but with irregular gaps. As \(n\) increases, the differences between consecutive terms can become very large.
Visualization
R Code & Visualization
funcionSecuenciaRecaman1<-function(numero) {
x<- vector()
y<- vector()
z<-0
i <- 1
while(i <= numero)
{
x[i] <- z
if(i == 1){
y[i] <- z
} else {
if(y[i-1] - x[i] > 0 & is.na(match(y[i-1] - x[i],y))) {
y[i] <- y[i-1] - x[i]
} else {
y[i] <- y[i-1] + x[i]
}
}
z<- z+1
i = i+1
}
return(cbind(x,y))
}
funcionSecuenciaRecaman1(25)
plottingChallenge<-function(numeral){
#Recaman Sequence: (only retrieving values)
laSecuencia <-funcionSecuenciaRecaman1(numeral)[,2]
#declarandoVectoresNecesarios
puntosEnx <- vector()
puntosEny <- vector()
ciclo <- vector()
degrees <- c(1:179) #to simulate semi-circle we will need degrees from 1 : 179
numeral2 <- numeral - 1
#Comienza el Ciclo
for(i in 1:numeral2)
{
##These are the edges of the semi-circle (diameter of circle)
x1<- laSecuencia[i]
x2<- laSecuencia[i+1]
##Evaluating whether semi-circle will curve upwards or downwards
if(i%%2 == 0){curvaturaHaciaArriba <- 1} else {curvaturaHaciaArriba <- -1}
radio <- abs(x2 - x1)/2 #radius of circle
if(x2>x1){puntoMedio <- x1+radio}else{puntoMedio <- x2+radio }
alturas<- sin(degrees*pi/180)*radio*curvaturaHaciaArriba #all heights
distancias <- cos(degrees*pi/180)*radio #all lengths
if(x2>x1){distancias1 <- sort(distancias,decreasing = F)
} else {distancias1 <- distancias}
puntosEnx <- c(puntosEnx,x1,distancias1 + puntoMedio,x2)
puntosEny <- c(puntosEny,0,alturas,0)
}
matriz<-cbind(puntosEnx,puntosEny)
matrizUnica<-unique(matriz)
par(bg="black")
plot(matrizUnica[,1],matrizUnica[,2], type = "l",
main = "Secuencia de Recaman",
xlab = "Seq. Recaman",
ylab = "",
col="white", #color del grafico
#col.axis = "white", #estos son los numeritos,
col.axis = "yellow", #titulos de los axis
cex.lab = 1
)
points( tail(matrizUnica[,1],1), tail(matrizUnica[,2],1), pch = 11, col = "yellow" )
title("Recaman Sequence", col.main = "white")
}
plottingChallenge(50)
plottingChallenge(100)
plottingChallenge(150)
plottingChallenge(200)
plottingChallenge(500)
plottingChallenge(1000)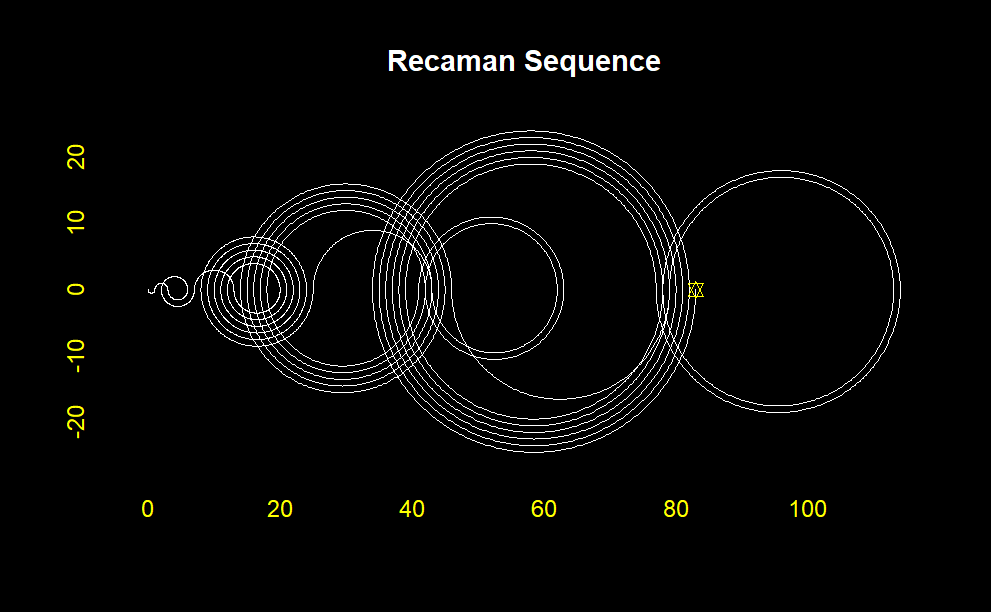
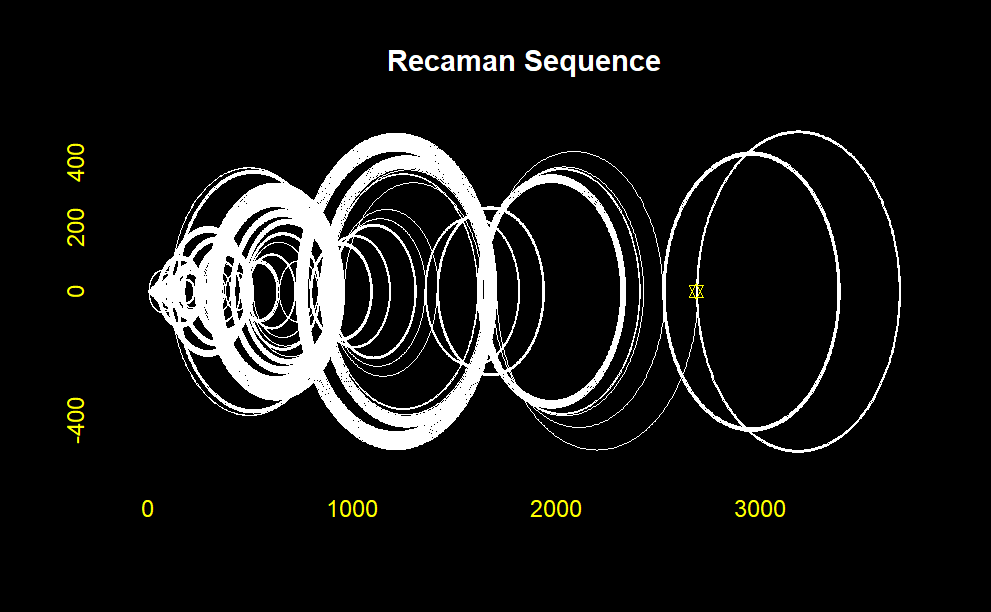
Recamán’s Sequence with tidyverse()
Clean and Effective Visualization
library(tidyverse)
# Generate the first n elements of the Recaman's sequence
get_recaman <- function(n) {
recaman_seq <- numeric(n)
for (i in 1:length(recaman_seq)) {
candidate <- recaman_seq[i] - i
if (candidate > 0 & !(candidate %in% recaman_seq)) {
recaman_seq[i + 1] <- candidate
} else recaman_seq[i + 1] <- recaman_seq[i] + i
}
recaman_seq <- recaman_seq[-length(recaman_seq)]
recaman_seq
}
get_recaman(20)
# Get semicircle paths
construct_arc <- function(start, stop, type) {
r <- abs(start - stop) / 2
x0 <- min(c(start, stop)) + r
y0 <- 0
if (type == "up_forward") {
theta <- seq(pi, 0, -0.01)
} else if (type == "up_backwards") {
theta <- seq(0, pi, 0.01)
} else if (type == "down_forward") {
theta <- seq(pi, 2 * pi, 0.01)
} else if (type == "down_backwards") {
theta <- seq(2 * pi, pi, -0.01)
}
x <- r * cos(theta) + x0
y <- r * sin(theta) + y0
df <- data.frame(x, y)
}
# Plot the first n elements of the Recaman's sequence
plot_recaman <- function(n, size = 1, alpha = 0.8) {
recaman_seq <- get_recaman(n)
df <- data.frame(start = recaman_seq,
stop = lead(recaman_seq),
# Alternating position of the semicircles
side = rep_len(c("down", "up"), length(recaman_seq))) %>%
mutate(direction = ifelse(stop - start > 0, "forward", "backwards"),
type = paste(side, direction, sep = "_")) %>%
filter(!is.na(stop))
l <- Map(construct_arc, start = df$start, stop = df$stop, type = df$type)
df2 <- do.call("rbind", l)
ggplot(df2, aes(x, y)) +
geom_path(alpha = alpha, size = size) +
coord_fixed() +
theme_void()
}
plot_recaman(100, size = 2)
plot_recaman(300, size = 1)
plot_recaman(500, size = 0.5, alpha = 0.8)
plot_recaman(1000, size = 0.5, alpha = 0.8)
plot_recaman(1500, size = 0.5, alpha = 0.8)
plot_recaman(2000, size = 0.5, alpha = 0.8)
# Do you like the drawing? Save it!
#ggsave("Recamán's sequence.png", height=3, width=5, units='in', dpi=800)
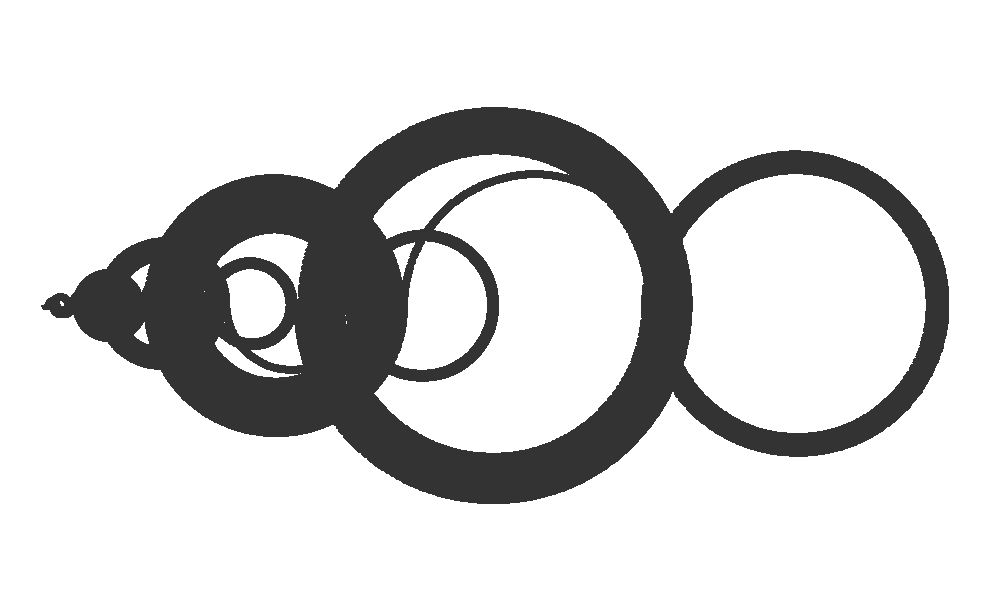
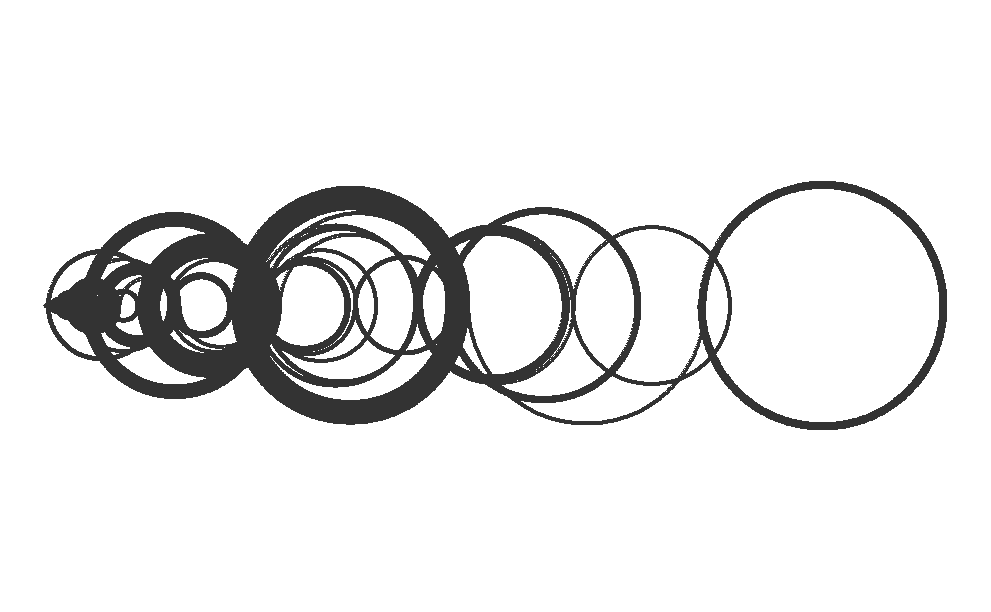
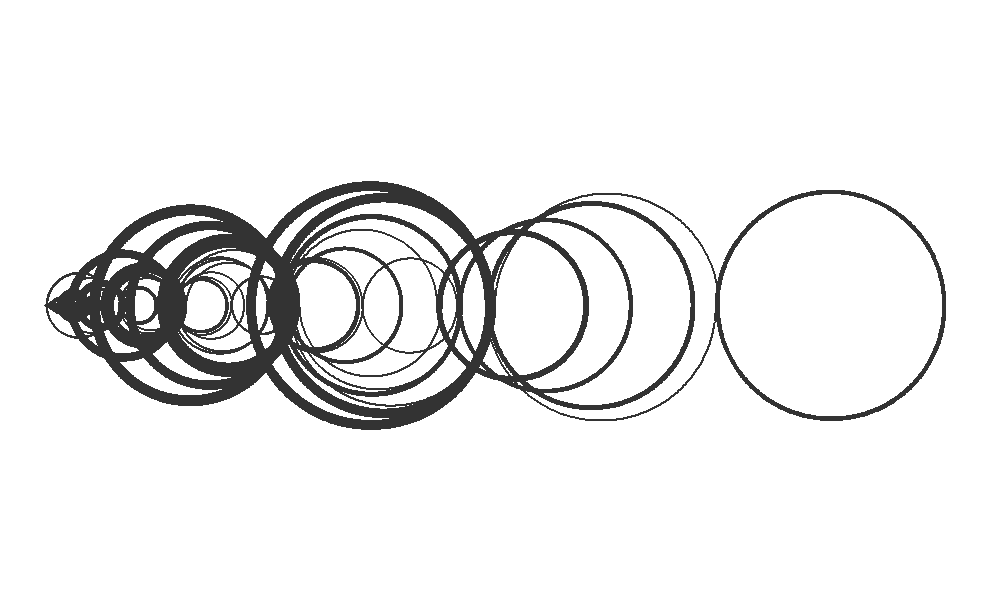
Symmetry in Motion: Exploring Artistic Patterns Through Mathematical Curves
Unveiling the Beauty of Complex Curves
In the world where art meets mathematics, the concept of symmetry stands as a bridge between visual beauty and mathematical elegance. The exploration of wallpaper patterns is a testament to this harmonious convergence. Inspired by Frank A. Farris’s book “Creating Symmetry: The Artful Mathematics of Wallpaper Patterns,”

this article delves into the intricate and astounding mathematics that underpins these seemingly simple designs. Through the lens of R programming, we will embark on a journey to uncover the hidden symmetries and patterns that adorn walls and fabrics around the world.
Complex Exponential and Rotations in the Complex Plane
The fundamental mathematical operation in the code involves complex exponentials. Given a complex number \(z(t)\) represented as:
\[ z(t) = re^{i\theta(t)} \]
where \(r\) is the amplitude (modulus) and \(\theta(t)\) is the phase (argument), this expression can be written as:
\[ z(t) = r\Big(\cos( \theta(t)) + i \sin(\theta(t))\Big) \]
In the code, each circle is defined by:
\[ z_{\text{circle}}(t) = \text{amp} \times i^{\text{freq} \times t+ \text{phase}} \]
where \(i^{\theta} = e^{i\theta}\) (using Euler’s formula)
This represents a rotation in the complex plane:
\[ z_{\text{circle}}(t) = \text{amp} \times \left(\cos(\text{freq} \times t + \text{phase}) + i\sin(\text{freq} \times t + \text{phase})\right) \]
The parameters:
Amplitude (
amp): The radius of the circle.Frequency (
freq): The speed and direction of rotation. Positive frequency rotates counterclockwise, while negative frequency rotates clockwise.Phase (
phase): The initial angle or offset.
Visualizing the Mystery Function
To introduce more complexity and mystery to our plot, we can add additional circular motions with varying amplitudes, frequencies, and phases to our existing circle. This approach results in more intricate and fascinating patterns. By plotting this function \(z(t) = it + 0.5i^{5t+1}\) we can observe the interplay between the linear and circular components, resulting in a unique and captivating shape. This approach demonstrates how simple modifications to complex functions can lead to rich and visually stunning patterns. The function \(z(t) = it + 0.5i^{5t+1}\) consists of two components:
The term \(1i\times t\) represents a linear increase in the imaginary direction, creating a spiral-like effect.
The term \(0.5 \times 1i^{5t+1}\) adds additional circular motion with an amplitude of \(0.5\), a frequency determined by \(5t\), and a phase shift of \(1\).
Let’s plot the function \(z(t) = it + 0.5i^{5t+1}.\)
Algorithmic Elegence
amp=0.5
freq=5
phase=1
z = 1i^t + # Our original circle
amp*(1i^(freq*t + phase)) # A new cirlce
plot(z, axes=FALSE, ann=FALSE, type="l", lwd=2, asp=1)
#____________________________________________________________________
# ~~~~~~~~~~~~~~ Animation ~~~~~~~~~~~~~~~~~~~~~~~~
library(gifski)
# Define the parameters
amp <- 0.5
freq <- 5
phase <- 1
t <- seq(0, 4, length.out = 1000)
# Define the function to generate the complex function with the given parameters
mystery_function <- function(t, amp, freq, phase) {
1i^t + amp * 1i^(freq * t + phase)
}
# Create the animation
save_gif(
lapply(seq(1, 1000, by = 10), function(j) {
z <- 1i^t + amp * 1i^(freq * t + phase)
plot(z, axes = FALSE, ann = FALSE, type = "l", lwd = 2, asp = 1)
lines(c(0, (1i^t)[j], z[j]), lwd = 3, col = "red")
points(c(0, (1i^t)[j], z[j]), cex = 2, pch = 20)
}),
delay = 1 / 30, width = 600, height = 600,
gif_file = "mystery_function_animation.gif")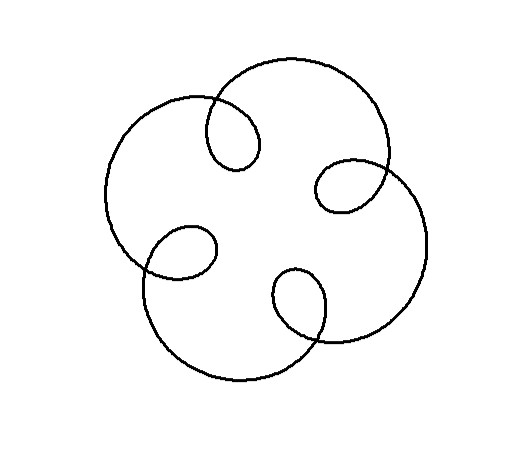
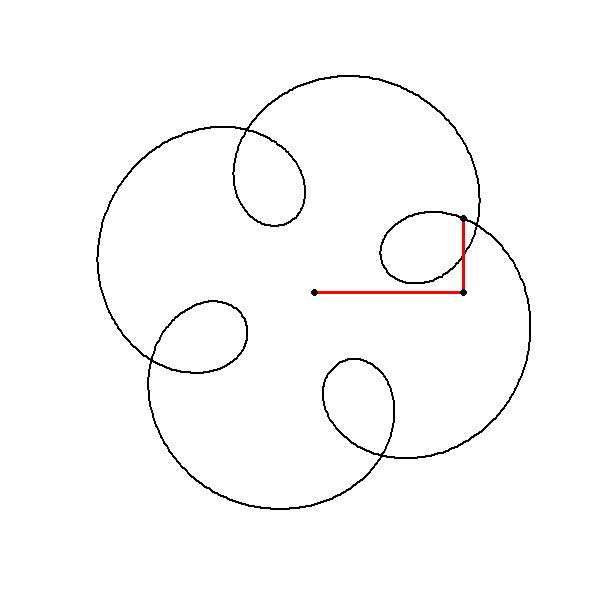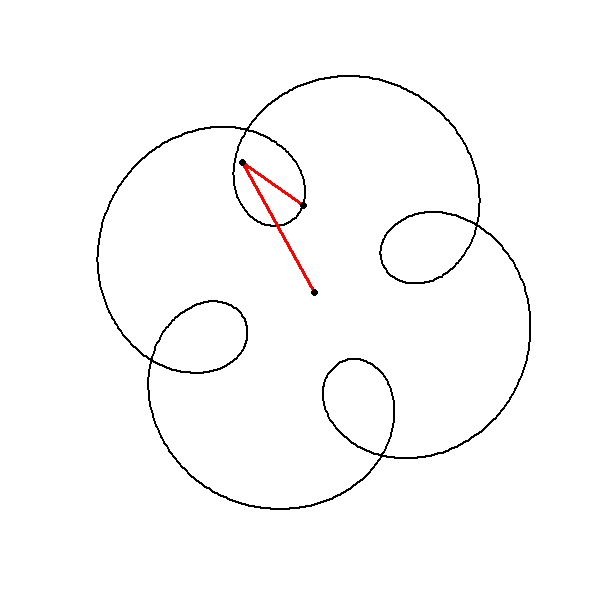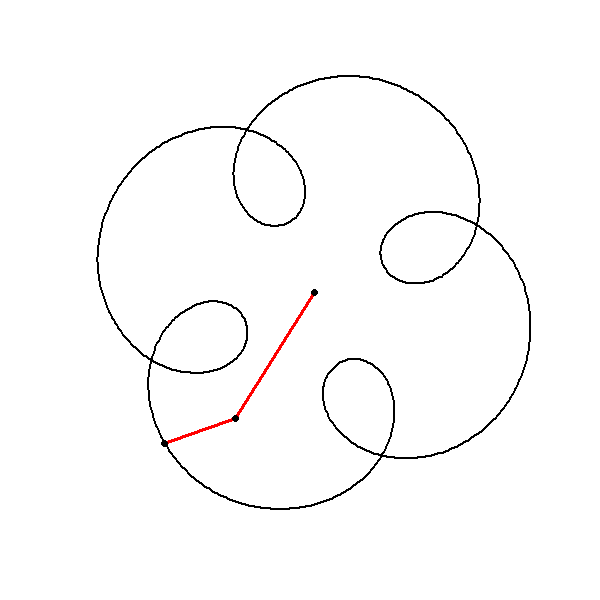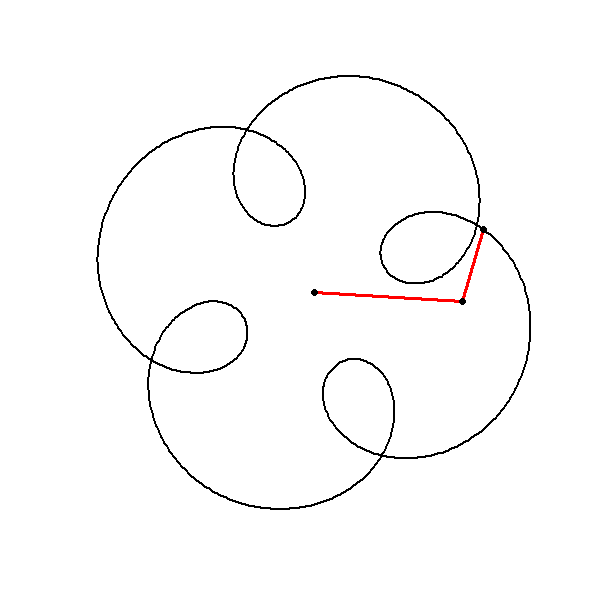
Combining Multiple Circles
Formal Algorithm
Input Parameters: Define the amplitudes, frequencies, and phases of the component circles.
Frequency Congruence: Ensure that all frequencies are congruent modulo \(N\) (here \(N=4\)).
Circle Function: Define the function for generating circles in the complex plane.
Sum of Circles: Compute the sum of the component circles.
Plotting: Plot the resulting complex function to visualize the symmetrical pattern.
Steps in the Code
Define Circle Function: \(circle(amp,freq,phase)=amp×1i^{(freq×t+phase)}\) where \(t\) is a sequence from \(0\) to \(4\), with \(1000\) points.
Sum of Circles: \(\text{z=circle(1,1,0)+circle(0.5,5,0)+circle(0.6,9,1)}\)
Plotting:
- Use
plotfunction to visualize the real and imaginary parts of \(z\) with appropriate settings for axes, annotations, line type, line width, and aspect ratio.
- Use
R Code & Algorithmic Elegance
circle <- function(amp, freq, phase) amp*1i^(freq*seq(0,4,l=1000)+phase)
z = circle(1,1,0) + circle(0.5,5,0) + circle(0.6,9,1)
plot(z, axes=FALSE, ann=FALSE, type="l", lwd=2, asp=1)
#____________________________________________________________________
# ~~~~~~~~~~~~~~ Animation ~~~~~~~~~~~~~~~~~~~~~~~~
library(gifski)
circle <- function(amp, freq, phase) amp * 1i^(freq * seq(0, 4, length.out = 1000) + phase)
save_gif(
lapply(seq(1, 1000, by = 2), function(j) {
z <- circle(1, 1, 0) + circle(0.5, 5, 0) + circle(0.6, 9, 1)
plot(z, axes = FALSE, ann = FALSE, type = "l", lwd = 2, asp = 1)
lps <- cumsum(c(0, circle(1, 1, 0)[j], circle(0.5, 5, 0)[j], circle(0.6, 9, 1)[j]))
lines(lps, lwd = 3, col = "red")
points(lps, cex = 2, pch = 20)
}),
delay = 1 / 30, width = 600, height = 600, gif_file = "circle_animation.gif"
)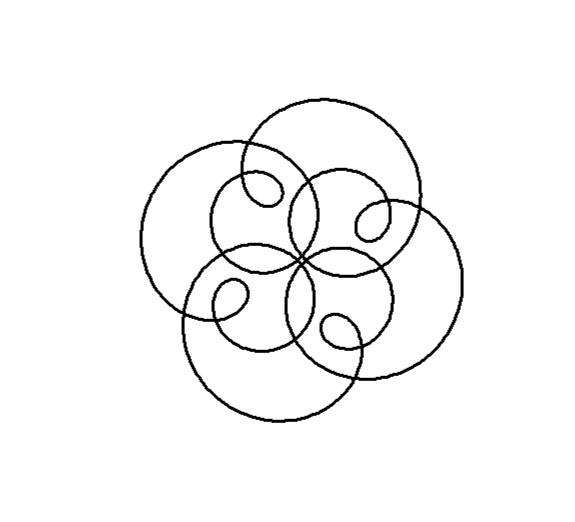
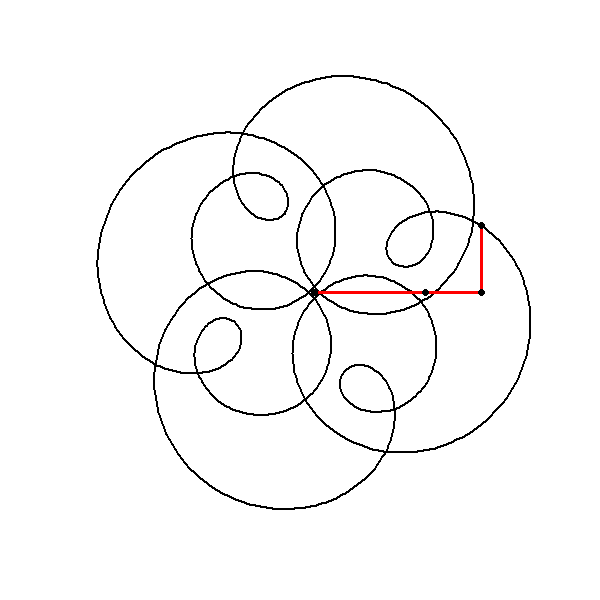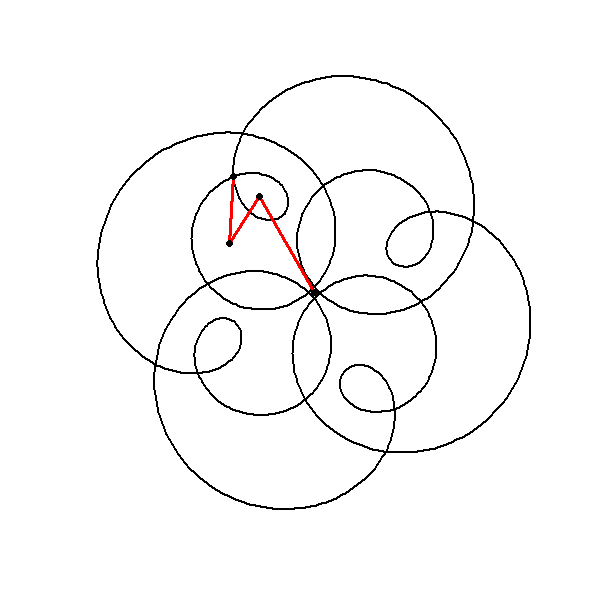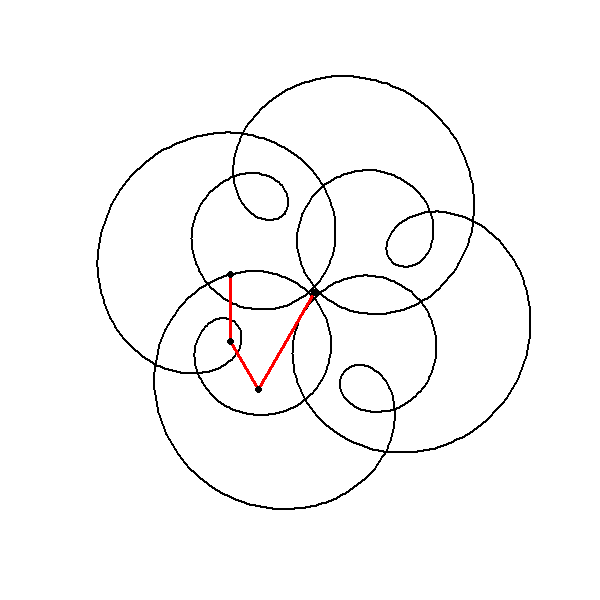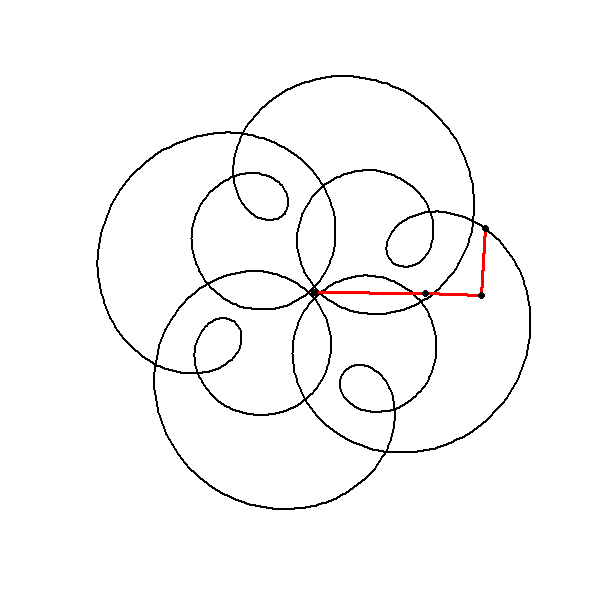
Revealing the Intricate Patterns
- Circle Function: The
circlefunction models each component as a complex exponential function.
\[ z(t) = \text{amp} \times i^{\text{freq} \times t+ \text{phase}} \]
- Combination of Circles: The total complex function
zis the sum of three such circular components.
\[ z(t) = \text{circle}(1, 1, 0) + \text{circle}(0.5, 5, 0) + \text{circle}(0.6, -7, 1) \]
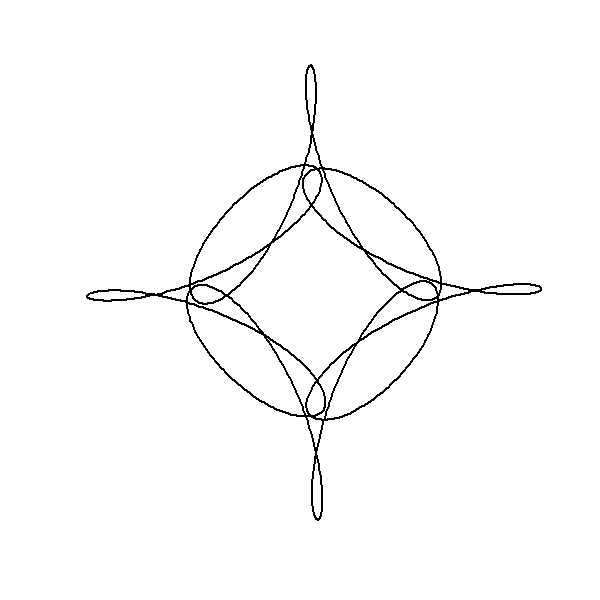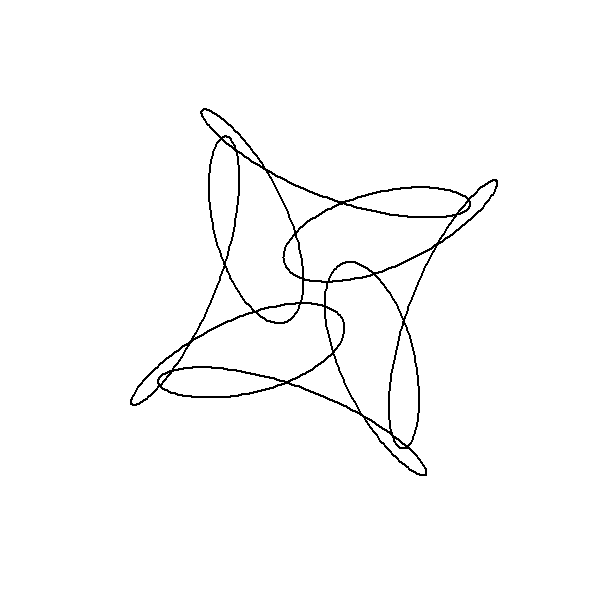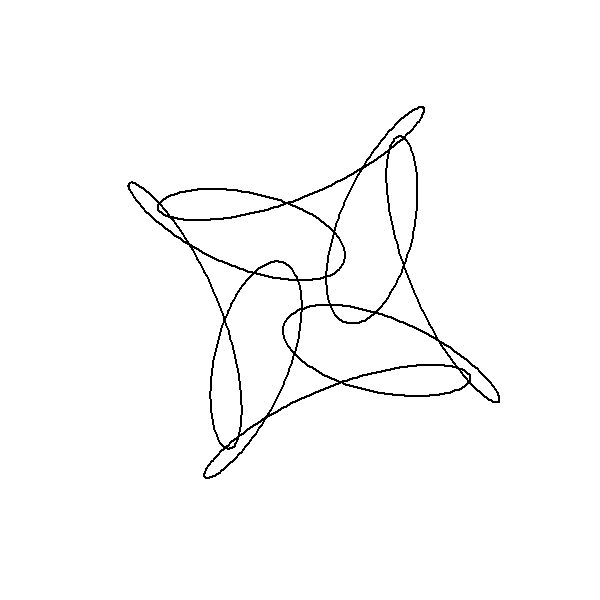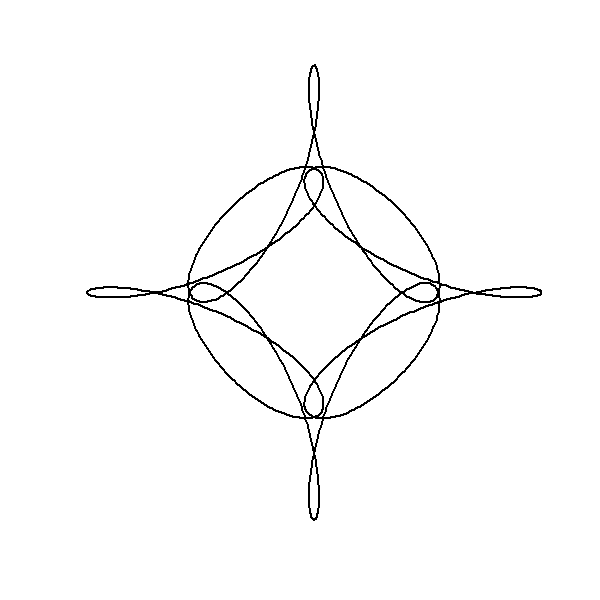
- Symmetry Considerations: Despite the differences in frequency, the use of congruent modulo arithmetic (as discussed earlier) ensures certain symmetries in the resulting pattern. For instance, the inclusion of a negative frequency still maintains the 4-fold rotational symmetry because \(-7 \mod 4 = 1\).
Visual Insight with Code
library(gifski)
circle <- function(amp, freq, phase) amp * 1i^(freq * seq(0, 4, length.out = 1000) + phase)
save_gif(
lapply(seq(1, 1000, by = 2), function(j) {
z <- circle(1, 1, 0) + circle(0.5, 5, 0) + circle(0.6, -7, 1)
plot(z, axes = FALSE, ann = FALSE, type = "l", lwd = 2, asp = 1)
lps <- cumsum(c(0, circle(1, 1, 0)[j], circle(0.5, 5, 0)[j], circle(0.6, -7, 1)[j]))
lines(lps, lwd = 3, col = "red")
points(lps, cex = 2, pch = 20)
}),
delay = 1 / 30, width = 600, height = 600, gif_file = "trajec_animation.gif"
)
Animation Insight with Code & Visualization
Algorithmic Approach
Frame Generation:
Plotting the Path:
Cumulative Sum (
cumsum):GIF Creation
Code Behind Creation of the Visual Representation
library(gifski)
circle <- function(amp, freq, phase) amp * 1i^(freq * seq(0, 4, length.out = 1000) + phase)
limits <- c(-1, 1) * 2
save_gif(
lapply(seq(0, 4, length.out = 100)[-1], function(j) {
z <- circle(1, 1, 0) + circle(0.5, 5, 0) + circle(0.6, -7, j)
plot(z, xlim = limits, ylim = limits,
axes = FALSE, ann = FALSE, type = "l",
lwd = 2, asp = 1, mar = c(0, 0, 0, 0))
}),
delay = 1 / 30, width = 600, height = 600, gif_file = "animation-circ.gif"
)
Visual Elegance of Butterfly Curve
The butterfly curve is defined using parametric equations. Parametric equations express the coordinates of the points that make up a curve as functions of a parameter, often denoted as \(t\). In this case, the curve is described using polar coordinates, which are defined in terms of a radius \(r\) (or \(a\) in the code) and an angle \(t\). The equations in the provided below are:
Radius Function \(a(t)\):
\[ a(t) = e^{\cos(t)} - 2 \cos(4t) - \sin\Bigg(\frac{t}{12}\Bigg)^5 \]
Parametric Equations for \(x\) and \(y:\)
\[ x(t) = a(t) \sin(t) \]
\[ y(t) = a(t) \cos(t) \]These equations define how the coordinates \(x\) and \(y\) of each point on the butterfly curve are determined by the angle \(t\) and the function \(a(t)\).
#butterfly curve
#t sequence of angles
t = seq(0,12*pi,0.001)#from 0 to 12*pi , increasing by 0.01
a = exp(cos(t)) - 2*cos(4*t) -sin(t/12)^5
# coordinates
x = sin(t)*a
y = cos(t)*a
#customizing the plot
#par is for parameters
#background black & margins removed
par(bg='black',mar=rep(0,4))
#adding gradient colors
#this is a function to generate gradient colors
color.gradient <- function(x,colors=c('red','yellow','green'),colsteps=100){
return(colorRampPalette(colors)(colsteps)[findInterval(x,seq(min(x),max(x),length.out=colsteps))])
}
#plot
#pch is point character (19 = dots)
#cex is to scale view
plot(x,y,type='p',col=color.gradient(x),pch=19,cex=1/9)#type = line
Symmetry: The butterfly curve displays symmetry, a characteristic feature that arises from the even and odd functions in its parametric representation.
Periodicity: The use of trigonometric functions introduces periodic behavior.
Mathematical Blossoms
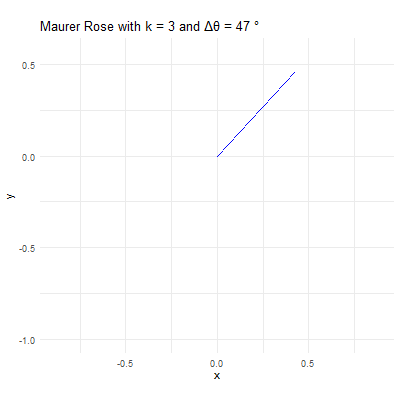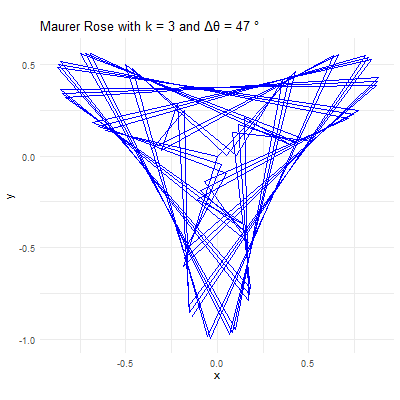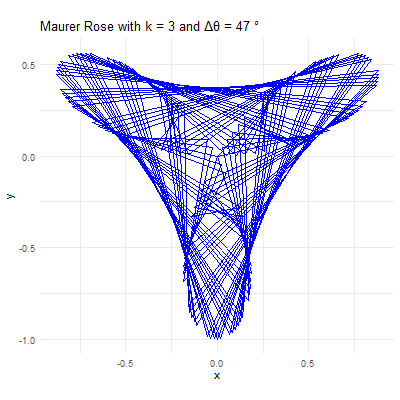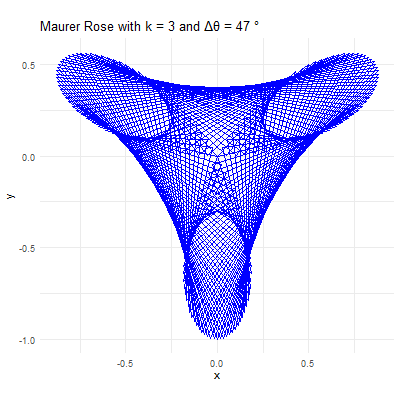
Maurer Rose
In exploring the artistic potential of mathematical functions, one can introduce a unique form of embellishment by plotting points out of their natural sequence and connecting them with lines. This method adds an element of visual complexity and interest to the underlying mathematical structure. Mathematically, this process is analogous to the construction of a Maurer rose, where points are plotted out of order on a rose curve, but here, we apply the technique to a more complex, “mystery” curve.
The Maurer rose is a mathematical curve, specifically a type of rose curve, named after the German engineer Peter Maurer who first described it in 1987. The Maurer rose is created by plotting a set of points on a polar coordinate system, connecting them with straight lines rather than the smooth curve typically associated with rose curves. The result is a mesmerizing pattern that can vary from simple, delicate designs to complex and intricate structures, depending on the parameters used.
The Mathematical Foundation
To understand a Maurer rose, we must first understand the rose curve, which is defined by the polar equation:
\[ r(θ)=a⋅\sin(kθ) \]
or
\[ r(\theta) = a . \cos(k\theta) \]
Here, \(r(\theta)\) is the radius as a function of the angle \(\theta\), \(a\) is a scaling factor, and \(k\) is a positive integer that determines the number of petals in the rose. If \(k\) is odd, the curve will have \(k\) petals, and if \(k\) is even, the curve will have \(2k\) petals.
The Maurer rose is generated by taking this rose curve and connecting points on it with straight lines at certain angular increments. Specifically, the points are selected at angles that are multiples of a fixed angle \(\Delta\theta\), usually expressed in degrees. The equation governing the Maurer rose is given by:
\[ P_i = (r(\theta_i),\theta_i)\; \text{where}\; \theta_i = i. \Delta \theta \]
In Cartesian coordinates, this can be expressed as:
\[ x_i = r(\theta_i).\cos(\theta_i) \]
\[ y_i= r(\theta_i). \sin(\theta_i) \]
The curve is drawn by connecting the points \(P_i\) with straight lines, where \(i\) ranges from \(0\) to a specified upper limit, forming a closed or open figure depending on the values of \(k\) and \(\Delta\theta\).
Exploring Patterns with Different Parameters
The beauty of the Maurer rose lies in the diversity of patterns that can be generated by varying the parameters \(k\) and \(\Delta\theta\). Here’s how different choices of these parameters affect the resulting pattern:
Parameter \(k\): This integer determines the basic shape of the rose curve. A small \(k\) value will produce a simple rose with a few petals, while larger \(k\) values create more complex structures. For instance, with \(k=2\), the rose has \(4\) petals, and with \(k=5\), it has \(5\) petals.
Angle \(\Delta\theta\): This angle defines how the points are spaced around the rose. When \(\Delta\theta\) is a small angle (e.g., \(1°\) or \(2°\)), the points are closely spaced, creating intricate and dense patterns. When \(\Delta\theta\) is larger (e.g., \(10°\) or \(15°\)), the points are more widely spaced, resulting in more open and less complex designs.
For example, consider \(k=7\) and \(\Delta\theta = 36^{0}\). The resulting Maurer rose will have a pattern where lines intersect to create a star-like shape. If \(\Delta\theta\) is changed to \(5°\), the figure becomes more intricate, with many lines crossing and weaving to form a much denser pattern.
General Algorithm for Generating a Maurer Rose
1. Define the Problem
Objective: Generate a Maurer rose pattern by connecting points on a rose curve.
Inputs:
k: Number of petals in the rose curve.n: Number of points (or degrees) for calculation.Δθ (delta_theta): Angular increment between consecutive points.
Output: A visual representation of the Maurer rose, typically as a plotted graph or animation.
2. Set Up the Environment
Choose the Programming Language: Decide whether to use R, Python, or another language.
Import Necessary Libraries: Import libraries like
matplotlibfor Python orggplot2for R, and other relevant packages (e.g.,gifskifor R orgganimatefor R).
3. Define the Mathematical Functions
Rose Curve Formula: Implement the rose curve equation \(r(\theta) = \sin(k\theta)\) or \(r(\theta) = \cos(k\theta)\).
Convert to Cartesian Coordinates: Use the polar to Cartesian conversion:
\(x = r \cdot \cos(\theta)\)
\(y = r \cdot \sin(\theta)\)
4. Generate Points on the Curve
Calculate Angular Points:
- Create a sequence of angles \(\theta_i = i \cdot \Delta\theta\) for \(i = 0,1,2,\ldots,n-1\)
Compute Radii: Calculate the radius \(r_i = \sin(k \cdot \theta_i)\) for each angle \(\theta_i\).
Compute Cartesian Coordinates: Use the calculated radii and angles to determine the corresponding \(x_i\) and \(y_i\) coordinates.
5. Plot the Points
Initialize Plotting Area: Set up the plotting environment with equal aspect ratio to ensure the rose is not distorted.
Plot Points: Connect the points \((x_i, y_i)\) sequentially to create the Maurer rose pattern.
6. Implement Animation (Optional)
Frame Sequence: If animating, create a sequence of frames that reveal the points progressively.
Render Animation: Use an animation library (
gganimatein R orFuncAnimationin Python) to render the Maurer rose drawing over time.
7. Test and Validate
Test with Different Parameters: Try different values for
kandΔθto see the variations in the Maurer rose pattern.Edge Cases: Consider edge cases like
k = 1or very small/largeΔθ.
8. Optimize and Refactor
Optimize Performance: Ensure the code runs efficiently, especially if handling large
nor complex animations.Refactor Code: Simplify the code if possible, improving readability and maintainability.
9. Finalize and Save
Finalize Plot: Add titles, labels, and adjust aesthetics.
Save Output: Save the generated plot or animation to a file (e.g., PNG, GIF).
10. Document and Share
Comment the Code: Add comments explaining key parts of the code.
Share the Result: Provide the final output, including the code and the visual representation of the Maurer rose.
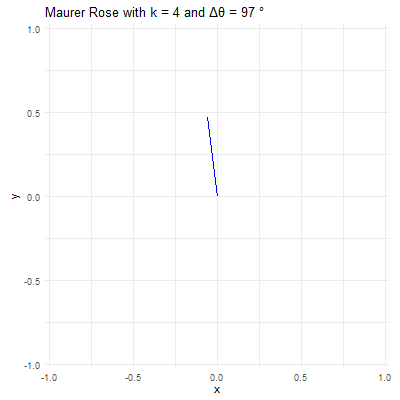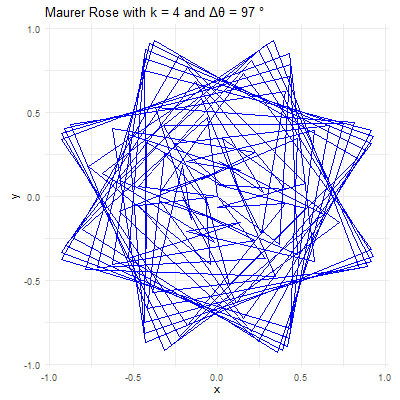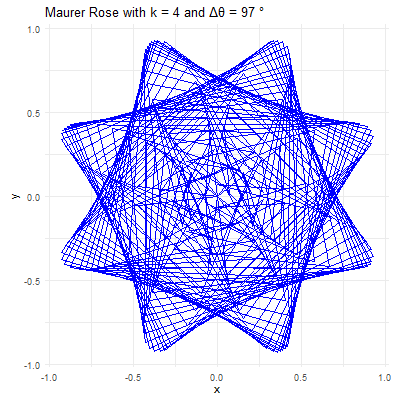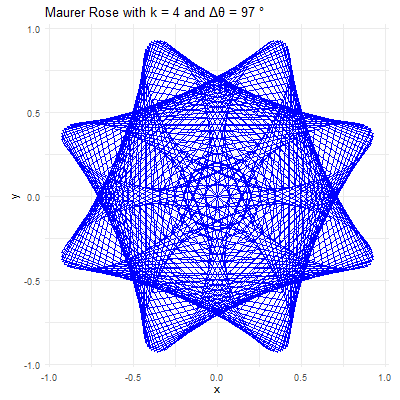
Visualizing the Maurer Rose
library(ggplot2)
library(gganimate)
library(gifski)
# Set parameters for the Maurer rose
k <- 4
n <- 360
delta_theta <- 97
# Generate the points
theta <- seq(0, n*delta_theta, by=delta_theta) * pi / 180
r <- sin(k * theta)
x <- r * cos(theta)
y <- r * sin(theta)
# Create a data frame to store the points
data <- data.frame(x = x, y = y, frame = seq_along(theta))
# Create the plot using ggplot2
p <- ggplot(data, aes(x = x, y = y, group = 1)) +
geom_path(color = "blue") +
coord_fixed() +
theme_minimal() +
ggtitle(paste("Maurer Rose with k =", k, "and Δθ =", delta_theta, "°"))
# Animate the plot using gganimate
anim <- p + transition_reveal(frame) +
ease_aes('linear')
# Save the animation as a GIF
anim_save("maurer_rose_8.gif", animation = anim, renderer = gifski_renderer(), width = 400, height = 400, duration = 10)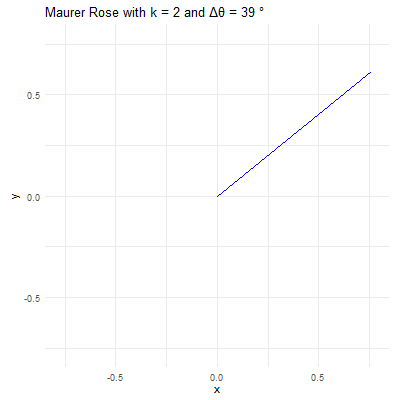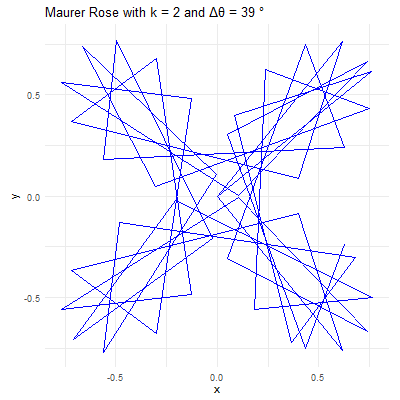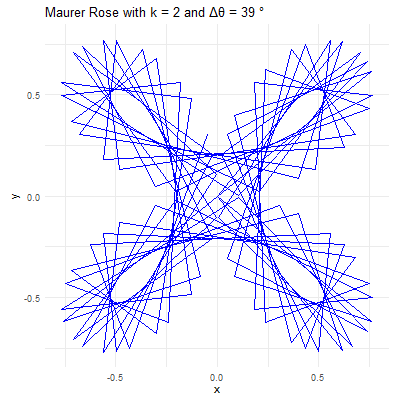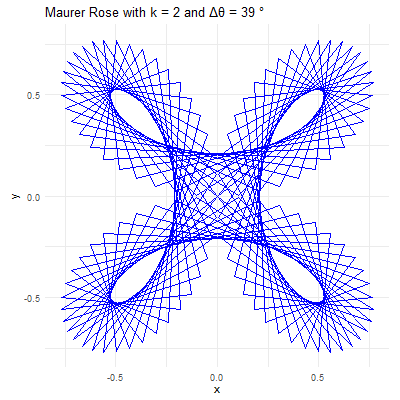
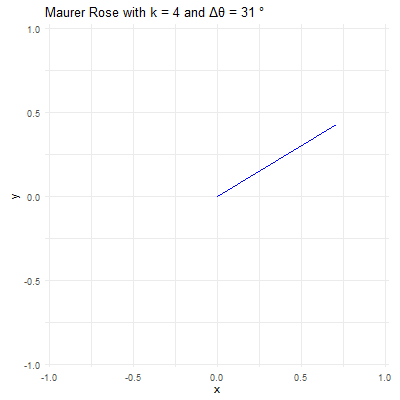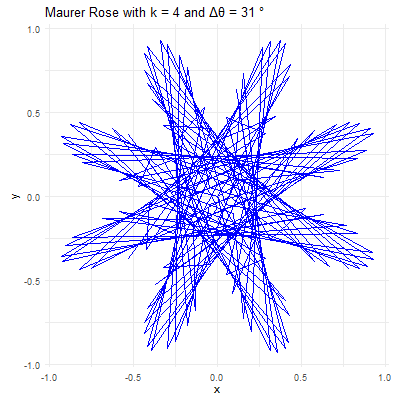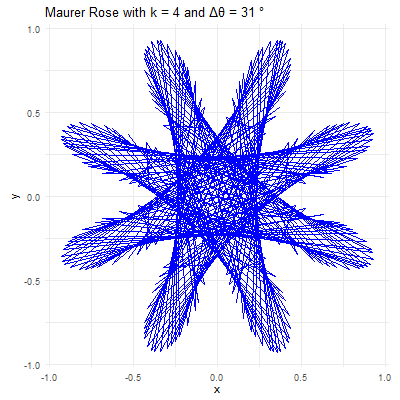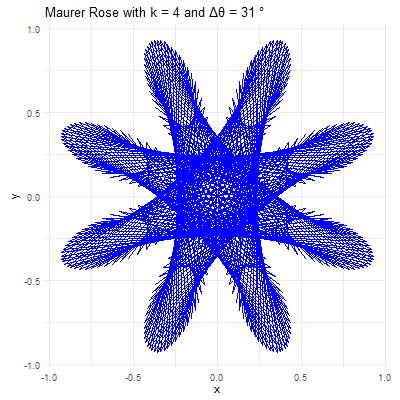
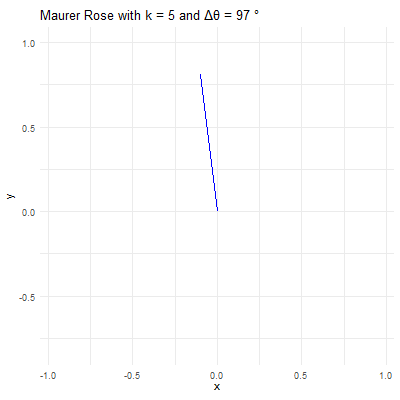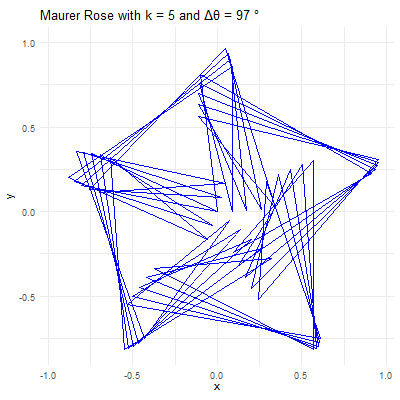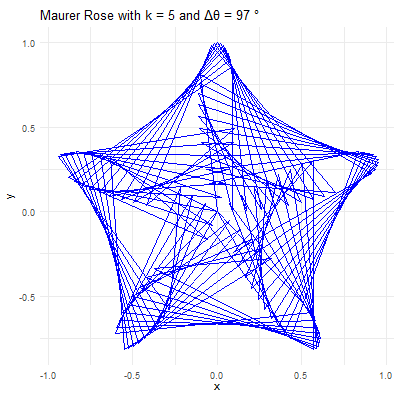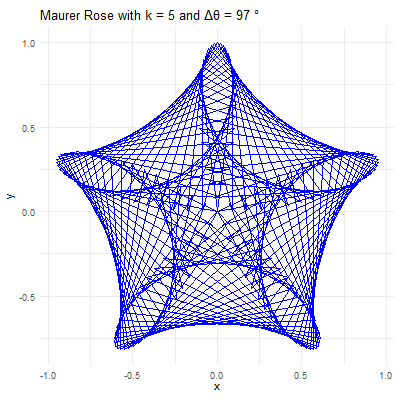
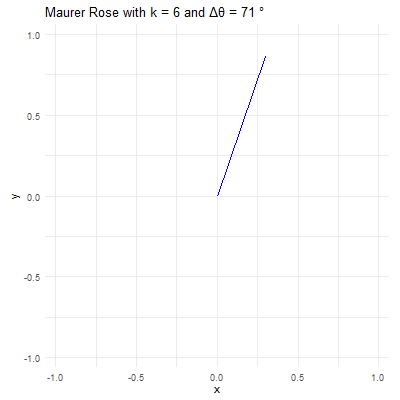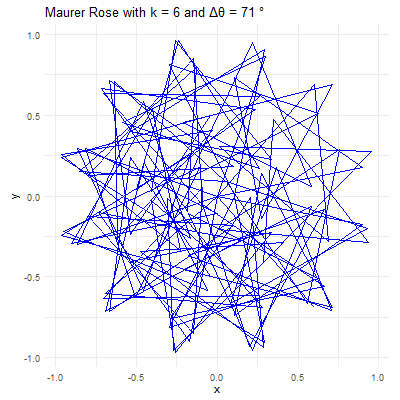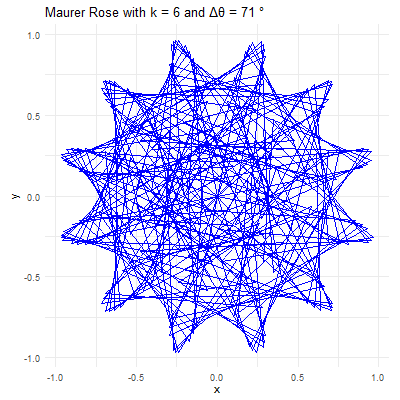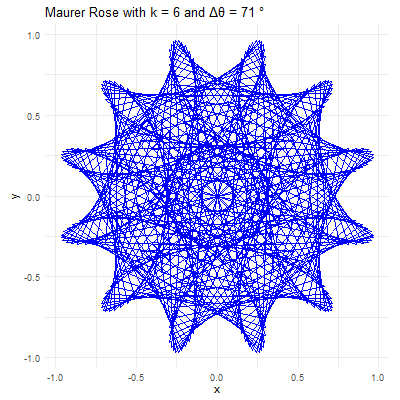
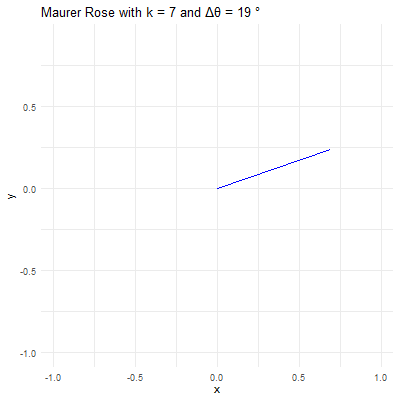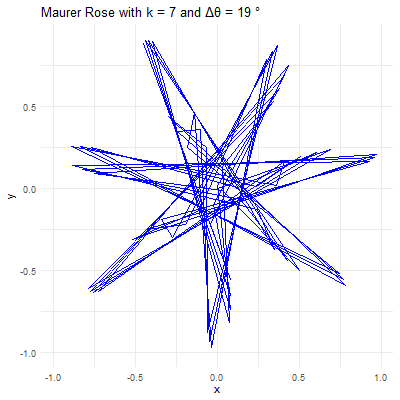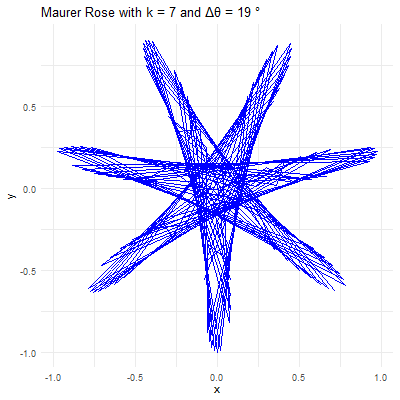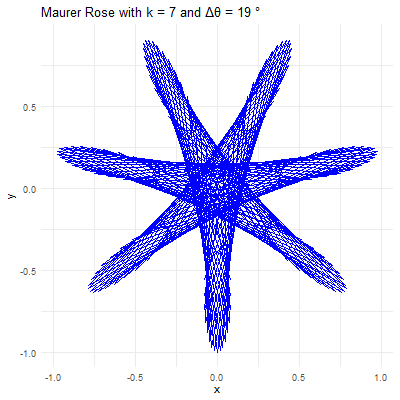
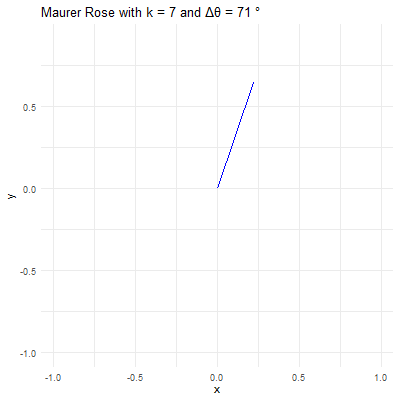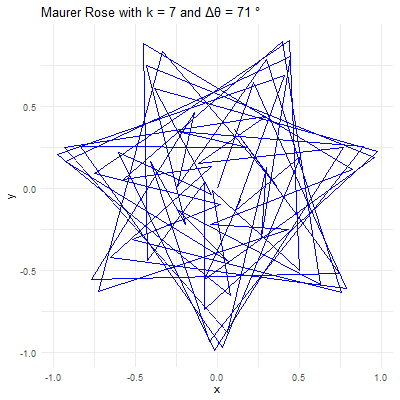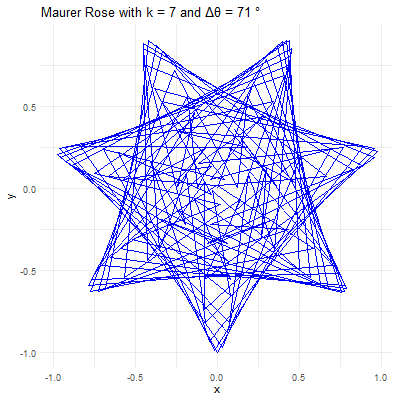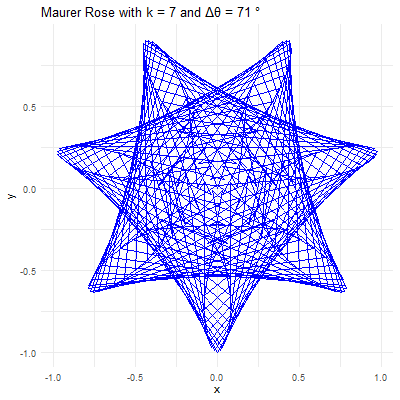
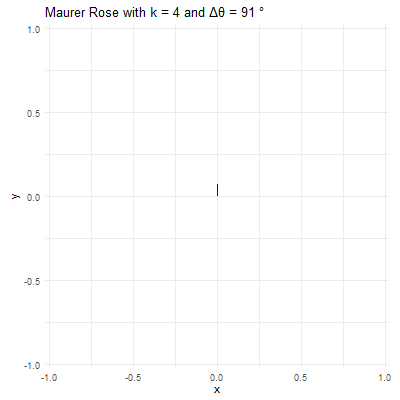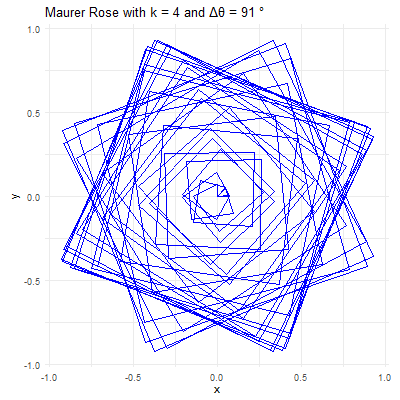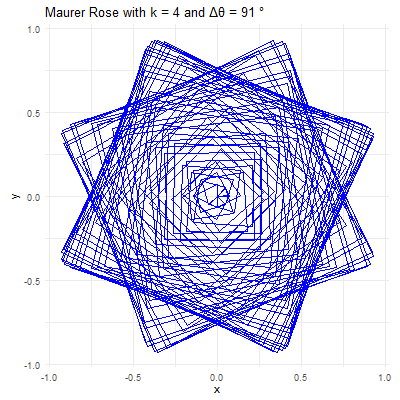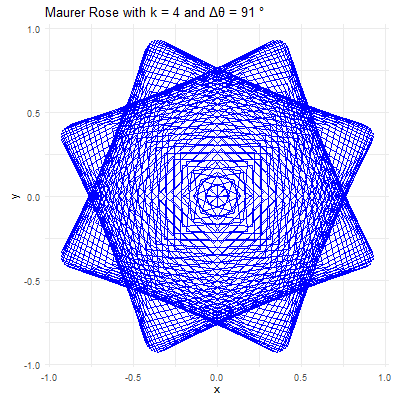
Revealing Hidden Symmetries & Patterns
Artistic Fact
Mathematical Fact:
Mathematical and Artistic Interplay in Plotting Out-of-Order Points
library(gifski)
circle <- function(amp, freq, phase) amp * 1i^(freq * seq(0, 400, length.out = 799) + phase)
limits <- c(-1, 1) * 3
save_gif(
lapply(seq(0, 4, length.out = 100)[-1], function(j) {
z <- circle(1, 1, 0) + circle(1, 6, 0) + circle(1, -9, j)
par(bg = "black", mar = c(0, 0, 0, 0)) # Set a black background
plot(
xlim = limits, ylim = limits, col = "cyan", pch = 20,
z, axes = FALSE, ann = FALSE, asp = 1
)
lines(z, col = hsv(0.7, 0.5, 1, 0.5)) # Connect points with lines
}),
delay = 1 / 30, width = 800, height = 800, gif_file = "circle_animation.gif"
)library(gifski)
circle <- function(amp, freq, phase) amp*1i^(freq*seq(0,400,l=799)+phase)
limits=c(-1,1)*2.5
# lapply here makes a 'list' of plots,
# save_gif turns this list into a gif
save_gif(lapply(seq(0,4,l=500)[-1],
function(j){
par(bg="black")
z = circle(1,1,0) + circle(sin(pi*j/2),6,0) + circle(cos(pi*j/2),-9,j)
hue = (j/4+seq(0,0.5,l=799))%%1
plot(xlim=limits, ylim=limits,col=hsv(hue,.8,1),pch=19,
z, axes=FALSE, ann=FALSE, asp=1, mar=c(0,0,0,0))
lines(z,col=hsv(hue[1],.5,1,0.4))
}),
delay=1/30,width = 800,height=800, gif_file = "mystery.gif")library(gifski)
circle <- function(amp, freq, phase) amp*1i^(freq*seq(0,600,l=260)+phase)
limits=3.5*c(-1,1)
li <- seq(0,1,l=500)[-1]
save_gif(lapply(1:length(li), function(ai){
a = li[ai]*5;
l = sin(pi*(2*a-.5))+1
z<-circle(1,1,0) +
circle(l, ceiling(a), -8*a) +
circle(l/2-1,ceiling(((-a+2.5)%%5)-5), -4*a)
par(mar=c(0,0,0,0), bg="#04010F")
hue=(a+(Re(z/10)))%%1
plot(z,
col=hsv(hue, 0.65,1),
pch=20, lwd=1, cex=1.5, type="p", axes=F,
xlim=limits, ylim=limits)
z2 <- c(z[-1], z[1])
segments(Re(z), Im(z), Re(z2), Im(z2),
col=hsv(hue, 0.65,1,.1), pch=20, lwd=1)
}), delay = 1/30, width=800, height=800, gif_file = "mystery2.gif")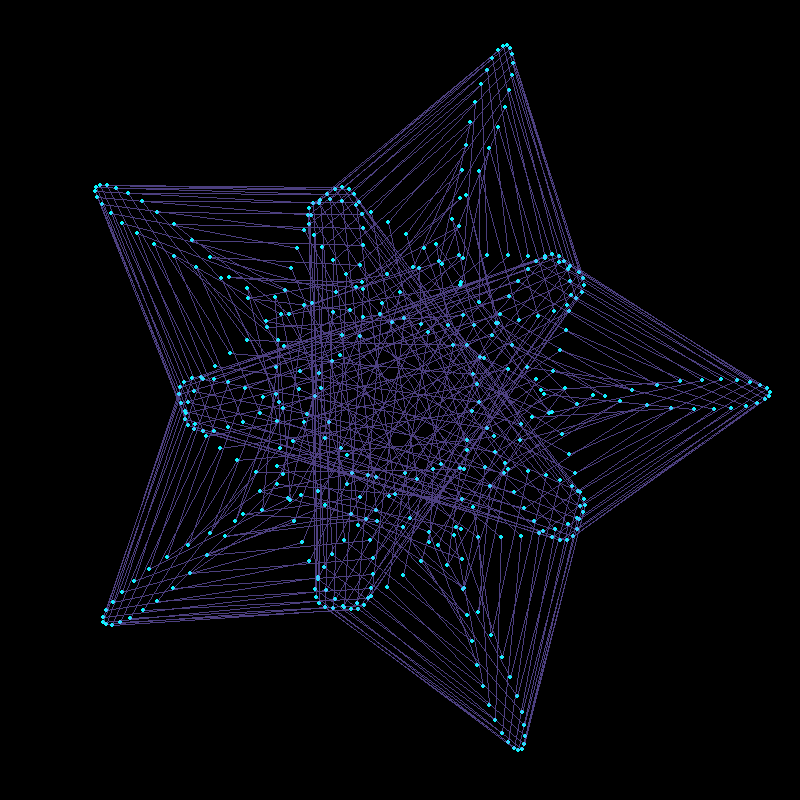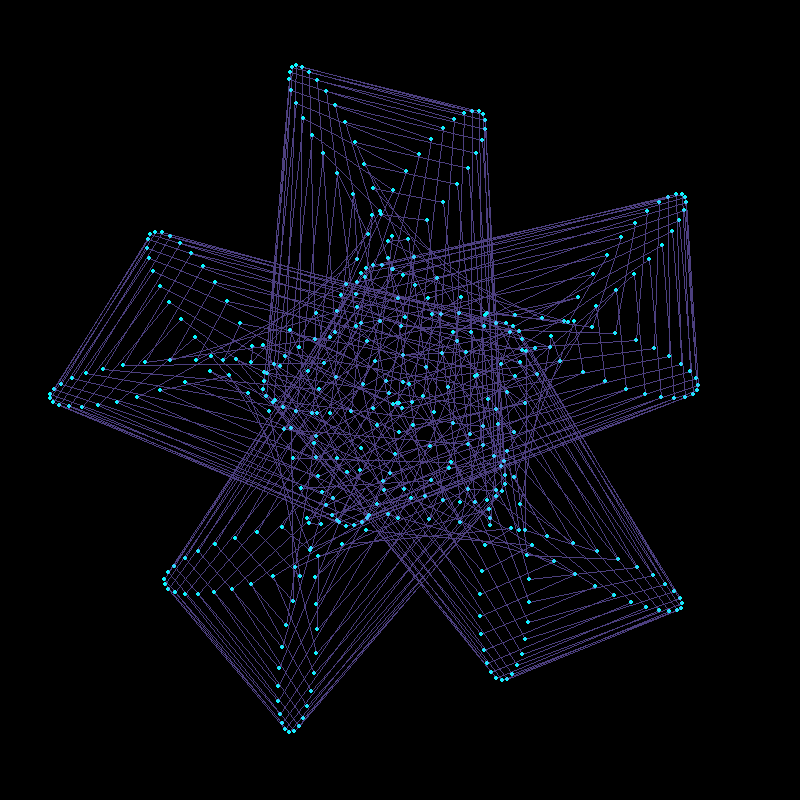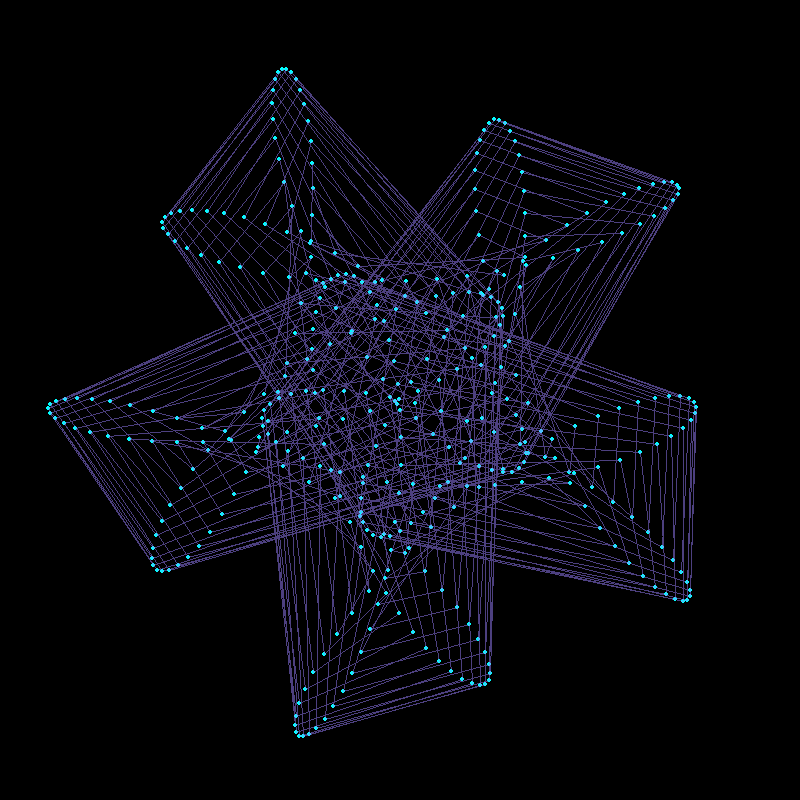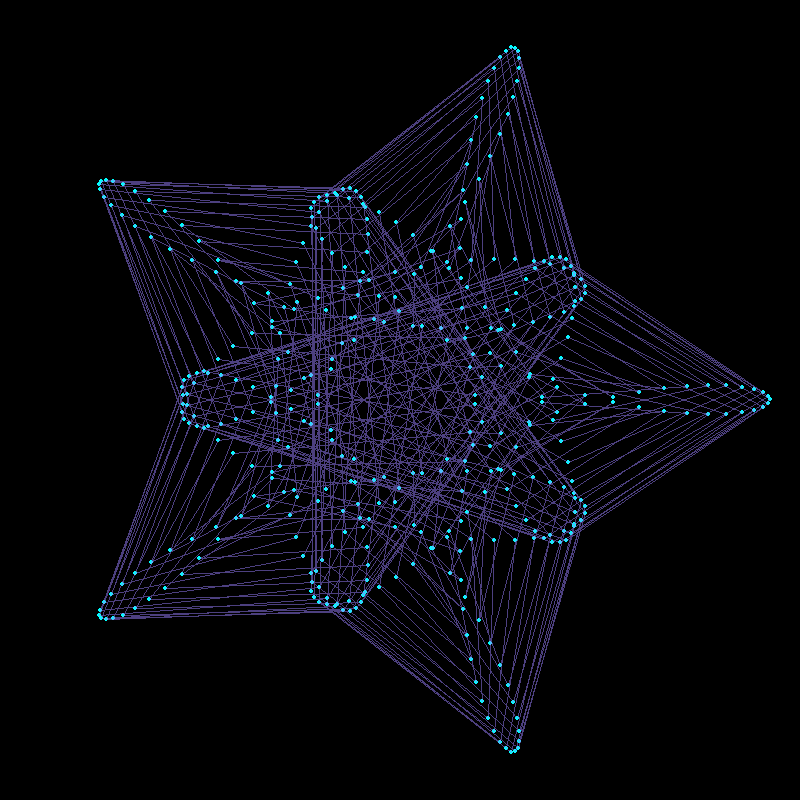
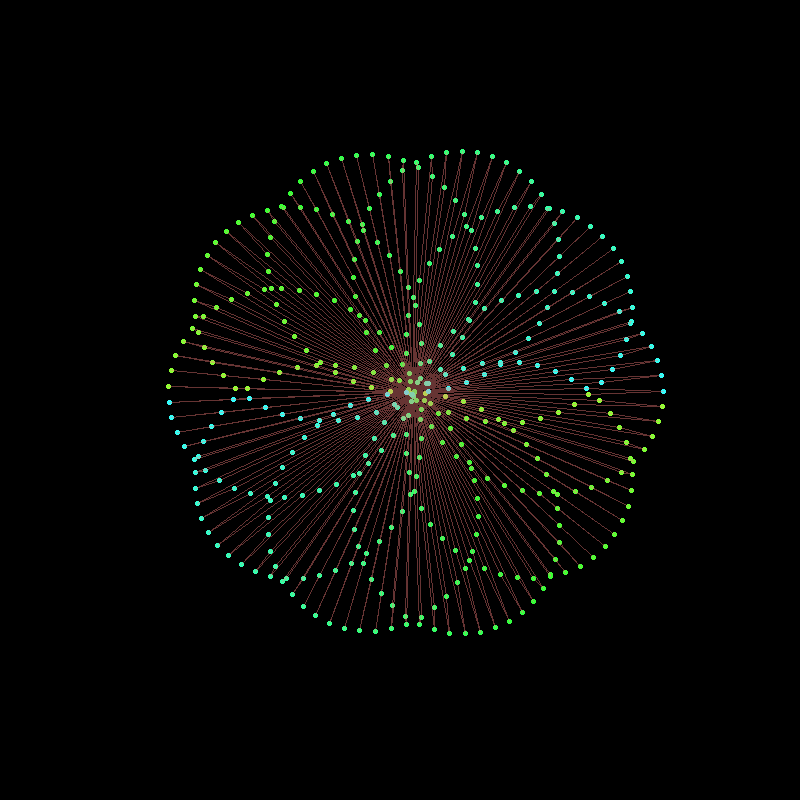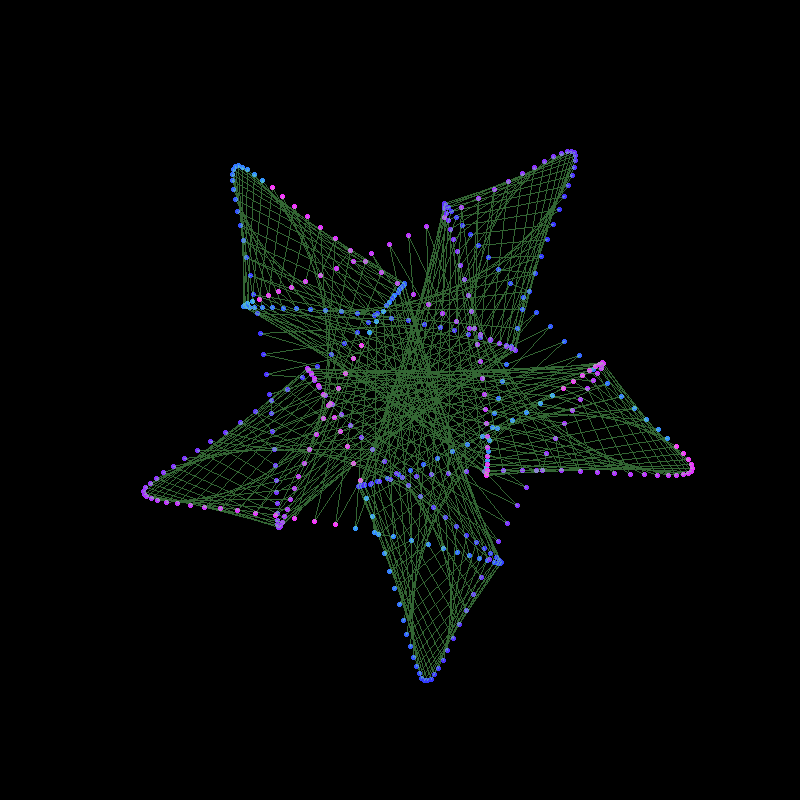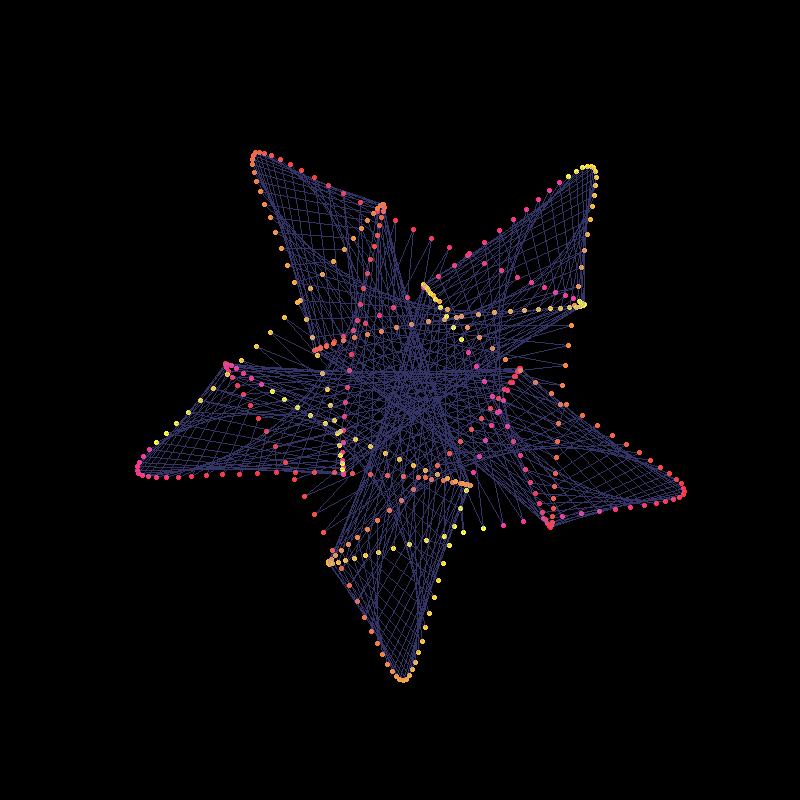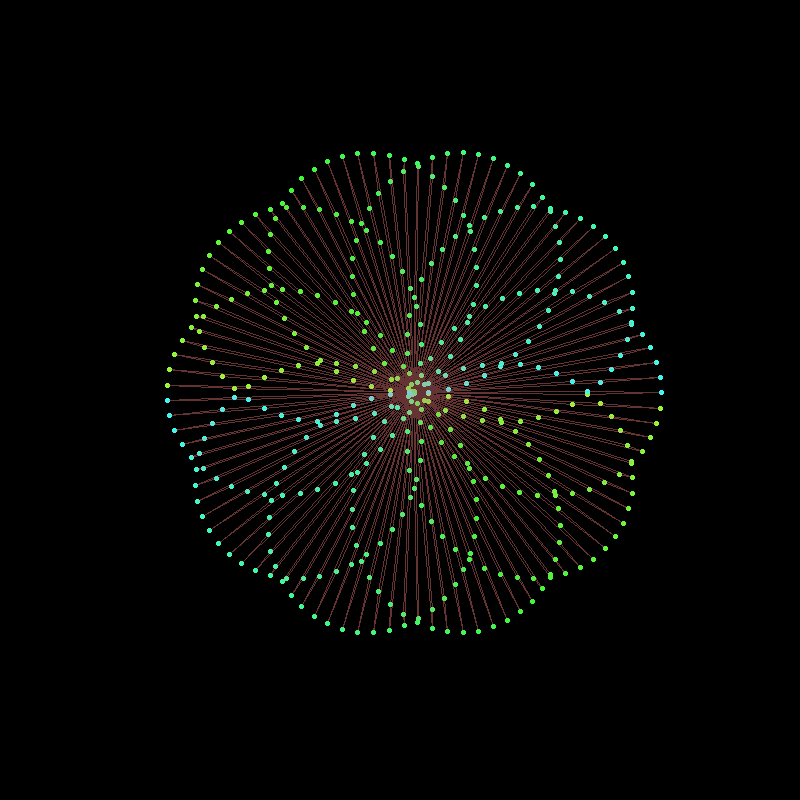
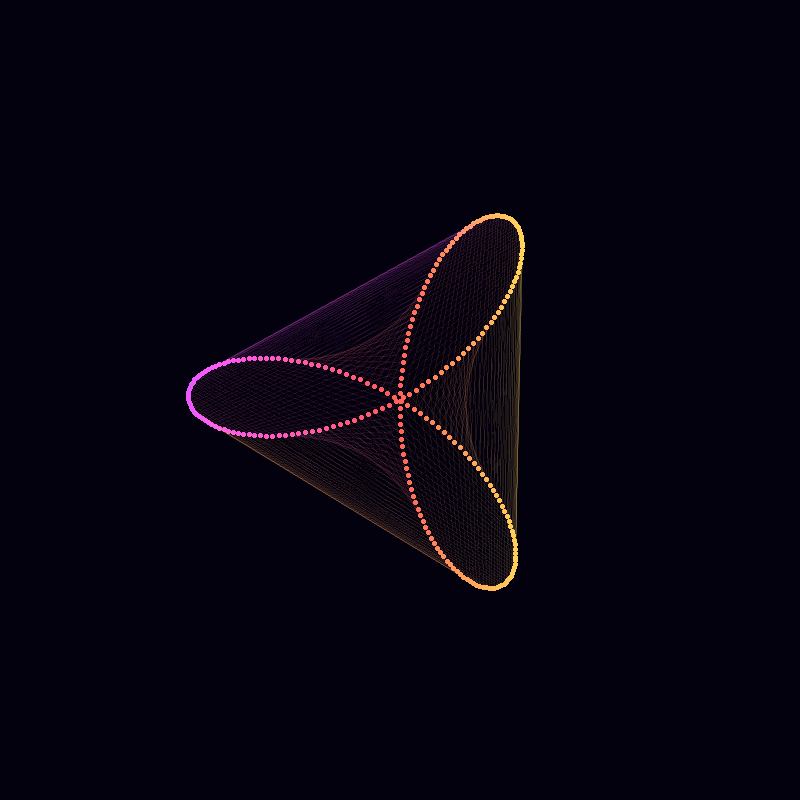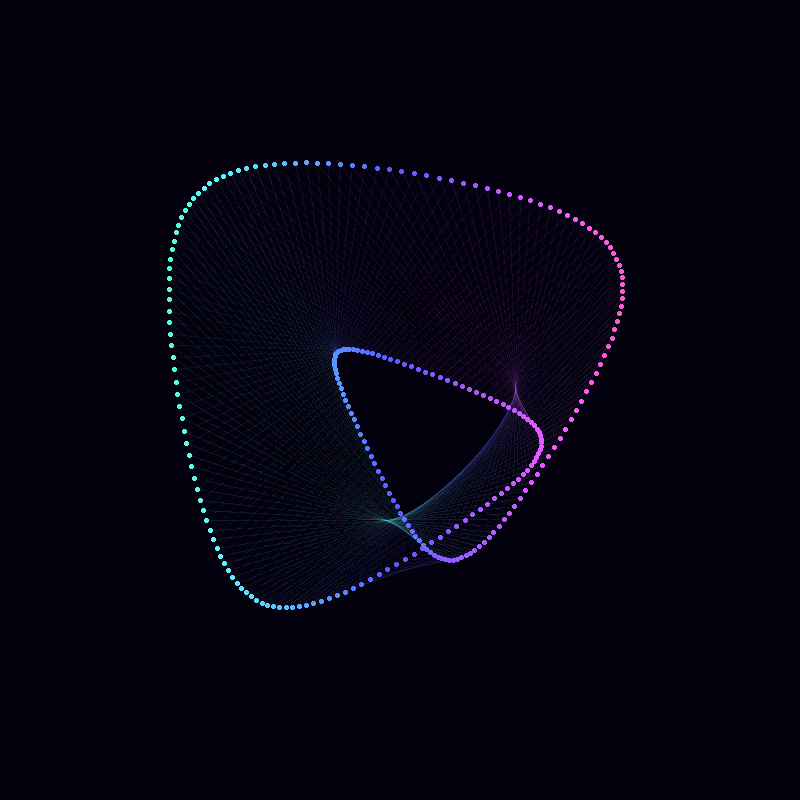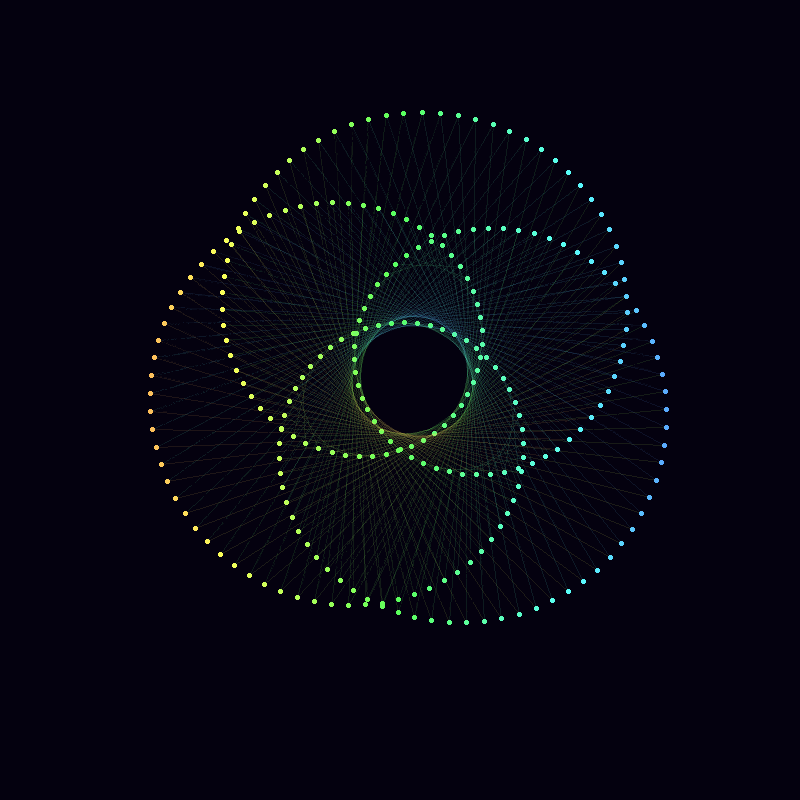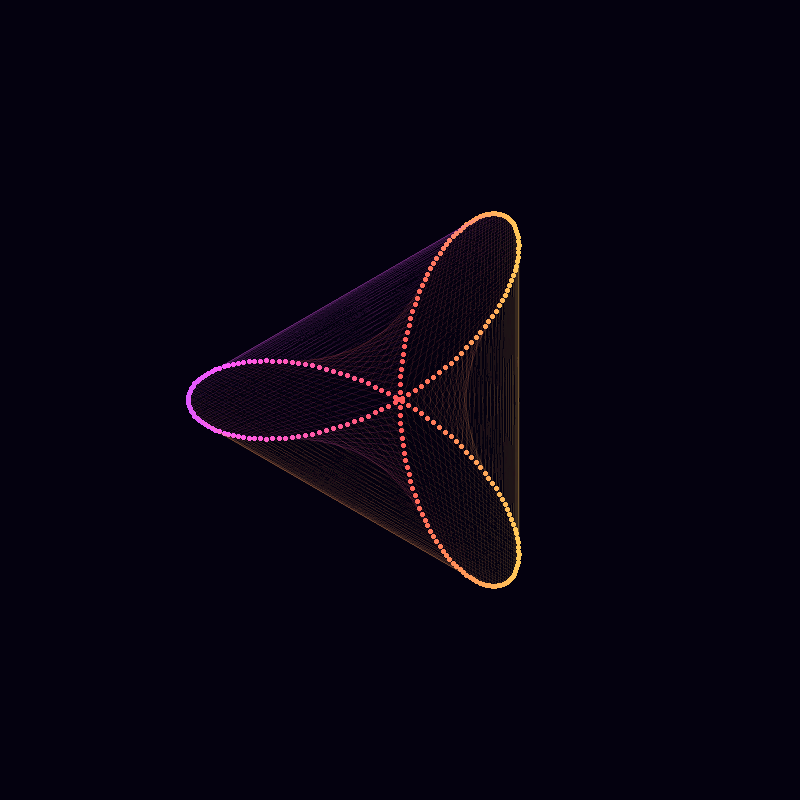
Conclusion
Demonstrating Beauty with Complexity
Creative Medium Bridges Mathematics and Art
Educational Tool
New Avenues for Research
Canvas for Creativity.
References
Thank You

https://abhirup-moitra-mathstat.netlify.app/