Indian Ragas as Probabilistic Spaces
A Measure Theoretic Perspective
Visiting Scholar at Vellore Institute of Technology (VIT-AP University)
Abstract
This paper proposes a novel measure-theoretic framework for analyzing Indian classical ragas. We model ragas as measurable spaces, where swaras, transitions, and aesthetic constraints correspond to elements in the Borel σ-algebra. Musical phrases are treated as measurable subsets, and their prominence is encoded via probability measures. Through solved examples, we apply these ideas to Raga Yaman and Raga Bhairavi, capturing their structural uniqueness analytically. This formalisation not only clarifies raga architecture but also extends mathematical music theory to non-Western systems, offering deeper insight into the interplay between abstract measure theory and the expressive logic of raga design.
Research Objectives
To formalize the structure of Indian classical ragas using the framework of measure theory.
To analyze the ascending aroha and descending avaroha patterns, permitted transitions, and emphasized notes of ragas through measurable spaces.
To establish parallels between the rules of raga performance and mathematical formal systems, particularly with Borel σ-algebras.
To investigate how measure-theoretic concepts can capture both deterministic rules and probabilistic variations in raga expression.
To develop a computational representation of ragas that preserves their emotional and aesthetic dimensions.
To explore interdisciplinary applications of this framework in algorithmic composition, computational modeling, and music analysis.
To contribute to a deeper mathematical understanding of artistic forms, bridging the gap between music theory and abstract mathematical structures.
Foundation of Measure Theory
The Basic Idea
When we talk about measuring a set, we mean assigning a number to a set that reflects its “size” in some sense.
For a line segment in R, the measure is its length.
For a rectangle in the plane, the measure is its area.
For a solid in 3D space, the measure is its volume.
So, “measure” generalizes the familiar notions of length, area, and volume to more abstract or complicated sets.
Measuring a Set
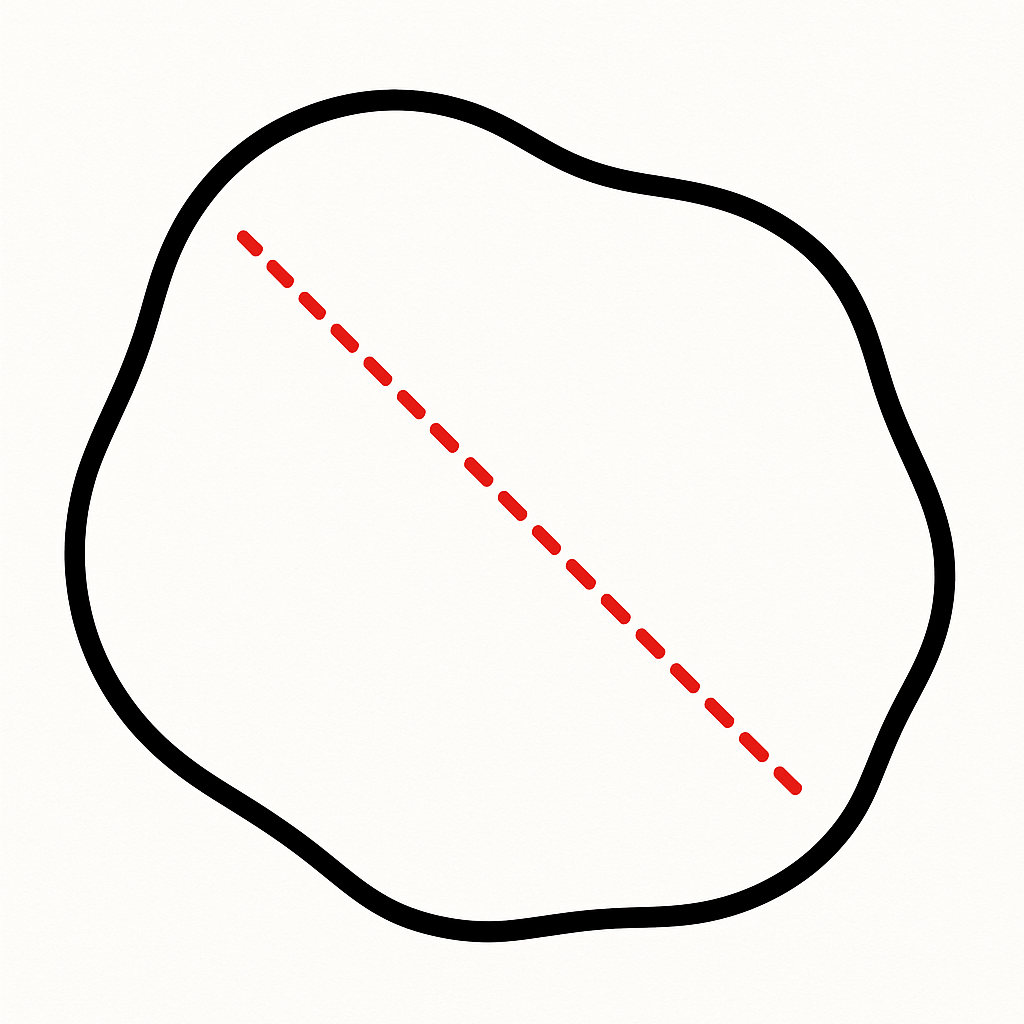
Longest Line Contained in the Set: Consider the length of the longest line that connects two points in the set and is completely contained within it.
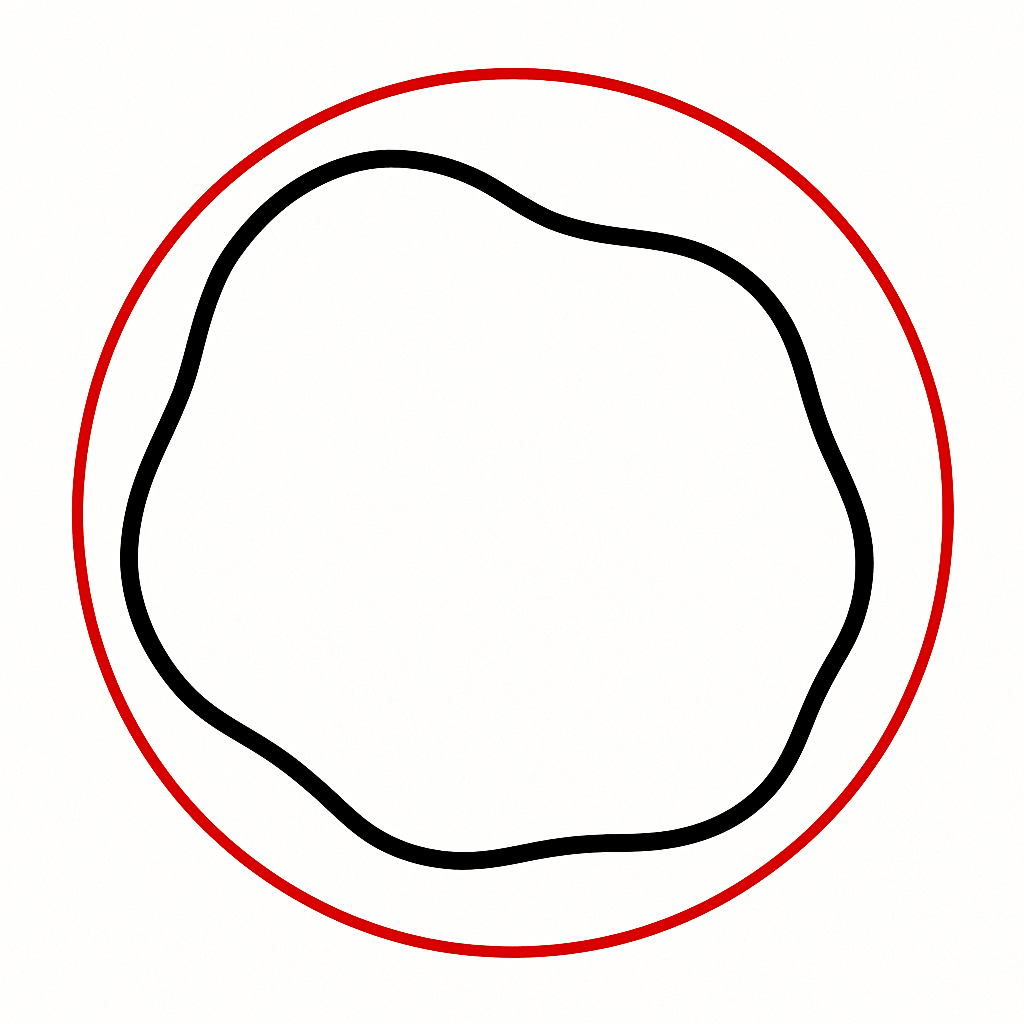
Smallest Enclosing Shape: Measure the area of the smallest circle in which the set can be inscribed.
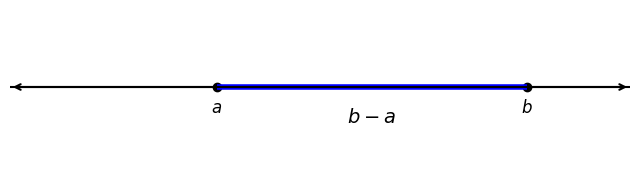
Let’s begin simply by considering subsets on the real line R. Suppose we want to measure such a subset. In the case of the real line R, this corresponds to a generalized length. For example, for an interval from a to b, the measure is the length b−a
The Science of Structure
Measure theory is the foundation of modern probability and analysis. At its heart lies the concept of a sigma-algebra (σ-algebra)—a collection of subsets that are closed under countable unions and complements. This structure allows us to rigorously define probability and integration, enabling us to measure the size of sets in a meaningful way.
A σ-algebra (sigma-algebra) is a collection of subsets of a given set that satisfies the following properties:
It contains the empty set ( ϕ ) and the universal set ( X ).
It is closed under complementation: If A∈A, then its complement Ac=X∖A is also in A.
It is closed under countable unions: If Ai∈A for i∈N, then ∞⋃i=1Ai∈A.
All systems of subsets that satisfy these three properties are called σ-algebras.
Consider the σ-algebra A={ϕ,X}. This is the smallest possible σ-algebra since:
The complement of each element is already in the set.
Any possible union of elements remains within the set.
The closure properties are trivially satisfied.
Thus, A={ϕ,X}} forms the smallest σ-algebra.
Measure theory formalizes the notion of size, length, and probability using a σ-algebra and a measure function. Given a set X and a σ-algebra A, a measure μ assigns a non-negative extended real number to subsets of X, satisfying properties like countable additivity.
A measurable space is a pair (X,A), where:
X is a set.
A is a σ-algebra on X, meaning:
X∈A.
If A∈A, then its complement Ac∈A.
If A1,A2,A3,⋯∈A, then their countable union ∞⋃n=1An∈A
A measure is a function μ:A→[0,∞] that satisfies the following properties:
Non-negativity: μ(A)≥0∀A∈A .
Null empty set: μ(∅)=0.
Countable additivity (σ-additivity): If {An} is a countable collection of disjoint sets in A, then
μ(∞⋃n=1An)=∞∑n=1μ(An).
The triplet (X,A,μ) is called a measure space.
Infinite Volume
In measure theory, we often encounter sets with infinite extent—such as R or N —and thus extend the positive real line with the symbol ∞. This yields the extended nonnegative real half-line:
[0,∞]=[0,∞)∪{∞}
The Raga: A Universe of Musical Possibilities
Ragas as Structured Musical Systems
In Indian classical music, a raga is much more than just a random collection of notes. It encompasses:
- A specific set of allowable swaras (notes),
- Directional rules such as Aroha (ascending) and Avaroha (descending),
- Emphasized or central notes like Vadi and Samvadi,
- Characteristic phrases known as pakads,
- Restrictions on permissible transitions between notes.
This structured framework aligns naturally with the mathematical idea of a σ-algebra, which organizes subsets of a set under specific closure properties.
Analogous Structure: σ-Algebras in Music
- Base Set (X): The set of all possible swaras (musical notes).
Note
Musical Notes as the Base Set: The swaras (notes) in Indian classical music, such as Sa, Re, Ga, Ma, Pa, Dha, Ni, can be thought of as the elements of a set X
- σ-Algebra (A): The collection of valid note combinations, characteristic phrases, and transitions which follow raga rules.
Note
Rules of a Raga: Just as a σ-algebra consists of specific subsets of X satisfying closure properties, the rules of a raga define permissible combinations of notes. Not all sequences of notes are allowed, just like not all subsets of a set are measurable.
- Measure(μ): A measure assigns a “size” to a subset, much like how different notes in a raga are emphasized differently.
Note
Weighting of Musical Importance: For instance, in Raga Yaman, the note Ma (Tivra Ma) has special prominence, just as some sets might have higher measure in probability theory.
- Closure Properties: These musical subsets remain closed under operations analogous to union, complement, and countable union, just like σ-algebras.
The Raga System: A Structured Infinity
From Notes to Measurable Sets
Indian classical music is built upon a framework of 12 fundamental notes (S, R, G, M, P, D, N, along with their variations like Komal and Tivra swaras). From this infinite spectrum of sound, musicians carefully select a finite subset of notes to construct a raga. Each raga is a sigma-algebra of sound—a constrained yet expressive selection from a larger space, forming a meaningful system of musical events. For example, consider the famous Bhairavi Raga, which consists of the notes:
From the total set of 12 notes, Bhairavi selects a subset of 7 notes, much like how a sigma-algebra selects meaningful events from an infinite space. The rules governing a raga—its ascent (Arohana), descent (Avarohana), and characteristic phrases—mirror the constraints imposed by measure theory when defining meaningful measurable sets.
Constructing a Probability Space
In probability theory, a probability space is a triplet (Ω,F,P), where:
Ω (Sample Space): The set of all possible outcomes.
F (Sigma-Algebra): A collection of measurable subsets of Ω, defining events to which probabilities can be assigned.
P (Probability Measure): A function that assigns a probability value to each event in F, following Kolmogorov’s axioms.
Axioms of a Probability Measure
P:F→[0,1] is a probability measure satisfying:
P(Ω)=1.
P(∅)=0.
P is countably additive: For disjoint sets A1,A2,A3,…,
P(∞⋃n=1An)=∞∑n=1P(An)
Interpreting Indian Raga via Mathematical Structures
Sample Space (Ω) → The Set of All Possible Notes & Phrases:
In the Indian classical tradition, a raga is not just a scale but a structured musical space, consisting of permissible notes (swaras), characteristic phrases (pakads), and melodic rules (lakshanas). Here, Ω represents all possible sequences of swaras and phrases that could theoretically be played.Sigma-Algebra (F) → The Set of All Measurable Musical Forms:
Not all combinations of notes form a valid raga. Just as sigma-algebras impose structure by selecting measurable subsets, a raga constrains its notes and phrases through ascending (Arohana) and descending (Avarohana) patterns, emphasized notes (Vadi, Samvadi), and expressive rules. These rules define which musical paths are permissible within the vast universe of tonal possibilities.Measure Function (P) → Assigning Importance to Notes & Phrases:
Each note and phrase in a raga carries a certain weight or probability based on its role. Some notes are played more frequently, while others appear as embellishments (gamakas). The measure function in probability assigns a likelihood to different events; similarly, a raga’s rules dictate how often and in what manner certain notes should be played. This transforms the raga into a probabilistic musical structure where improvisation is guided by a weighted musical landscape rather than randomness.
Modeling Raga Yaman using Measure-Theoretic Framework
- The Measurable Space
- Arohana and Avarohana Structure
- Defining the Measure μ
- Interpretation
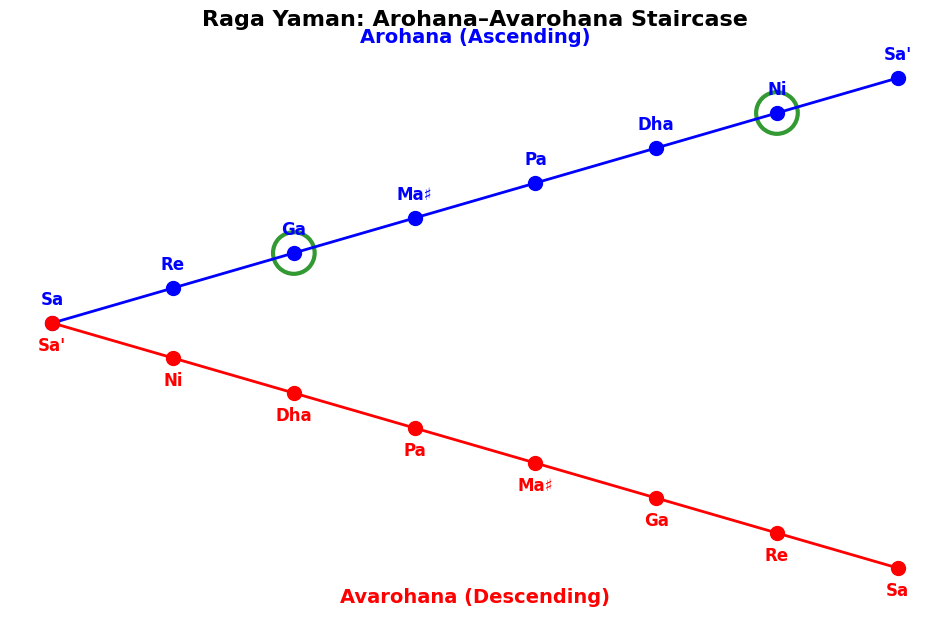
- Arohana–Avarohana Staircase
We define the measurable space (X,A) as follows:
Sample space (X): the set of all swaras (notes) across an octave.
X={Sa,Re,Re♯,Ga,Ga♯,Ma,Ma♯,Pa,Dha,Dha♯,Ni,Ni♯}
Raga Yaman specifically uses:
XYaman={Sa,Re,Ga,Ma♯,Pa,Dha,Ni}
- Ma♯ = Tivra Ma (sharpened fourth)
- All others are in Shuddha (natural) form
- Ma♯ = Tivra Ma (sharpened fourth)
Define A=P(XYaman), the power set, which is a σ-algebra over XYaman.
Arohana (ascending scale):
Sa → Re → Ga → Ma♯ → Pa → Dha → Ni → Sa′Avarohana (descending scale):
Sa′ → Ni → Dha → Pa → Ma♯ → Ga → Re → SaRepresent measurable subsets:
Aaroha={Sa,Re,Ga,Ma♯,Pa,Dha,Ni}
Aavaroha={Ni,Dha,Pa,Ma♯,Ga,Re,Sa}
Both are elements of A and represent valid measurable events.
Define μ:A→[0,1] to quantify musical importance.
In Raga Yaman:
- Vadi (prominent note): Ga
- Samvadi (second prominent note): Ni
- Vadi (prominent note): Ga
Assign weights:
μ({Ga})=0.25,μ({Ni})=0.20
μ({Ma♯})=0.15,μ({Sa})=0.10
μ({Re})=μ({Dha})=0.10,μ({Pa})=0.10
Total measure:
μ(XYaman)=∑x∈XYamanμ({x})=1
For any measurable set A⊆XYaman:
μ(A)=∑x∈Aμ({x})
- The σ-algebra A over the discrete set XYaman lets us treat melodic groupings as measurable sets.
- The measure μ reflects musical emphasis and structure.
- This formalism opens the way for analysis of ragas using probability, measure theory, computational musicology, and machine learning.
Conclusion
In the strains of a raga, we do not hear a fixed melody, but a probability space — a vast world of musical potential.
Just as measure-theoretic probability reveals hidden structure within randomness, the raga system unveils the deep architecture of sound, crafting order from chaos, measure from the immeasurable.
At its core, both the Indian raga system and measure theory share a principle:
Meaning emerges from structure.
Mathematics and music converge in their pursuit of harmony within infinite possibilities.
Measure theory, through sigma-algebras, rigorously defines the subsets of a space that can be meaningfully measured.
The raga system, through intricate rules and improvisation, carves out expressive subspaces from an ocean of sound.
The measure function in mathematics assigns weight to subsets, just as a raga assigns significance to each note, shaping:
Emotional depth.
Recurrence.
Role in the overall composition.
The connection between measure theory and Indian classical music is more than analogy — it is a profound truth.
Both disciplines show that constraints are not limitations, but frameworks within which infinity flourishes.
Whether in the silence of a theorem or the vibration of a sitar string, the same essence emerges:
within structure, the deepest creativity is born.
References
Cohn, Donald L. Measure Theory, Vol. 1, Springer, 2013.
Rao, B. Subba. Raga Nidhi. Music Academy of Madras, 1999.
Powers, H. S. Indian Music and the West. Oxford University Press, 2005.
Duxbury, S. P. The Interaction of Indian Music and Western Mathematical Principles.
Mathematics and Music: Proceedings of the First ESMA Conference, 2003.Benson, D. Music: A Mathematical Offering. Cambridge University Press, 2007.
Cope, D. Computer Models of Musical Creativity. MIT Press, 2005.
Tao, T. An Introduction to Measure Theory. American Mathematical Society, 2011.
Fremlin, D. H. Measure Theory, Vol. 2: Broad Foundations. Torres Fremlin, 2000.
Bogachev, V. I. Measure Theory. Springer, 2007.
Billingsley, P. Probability and Measure. John Wiley & Sons, 1995.
Lewin, D. Generalized Musical Intervals and Transformations. Oxford University Press, 2007.
Maheu, J. “Category theory and musical form: An application to post-tonal analysis.”
Journal of Mathematics and Music, vol. 17, no. 1, pp. 17–41, 2023.Michon, P.-Y. “A categorical framework for musical transformations.”
Journal of Mathematics and Music, vol. 15, no. 2, pp. 124–145, 2021.Chakraborty, S., and G. Saha. “Computational modelling and analysis of Indian classical music: A review.”
ACM Computing Surveys (CSUR), vol. 47, no. 2, pp. 1–38, 2014.Vishnubhotla, S., and X. Serra. “Raga recognition in Indian classical music using pitch-class distribution and recurrent neural networks.”
In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), 2022.
Further Readings
Moitra, A. Mathematical Aesthetics in Ragas. Ganit Charcha, 2025.
Available at: https://www.ganitcharcha.com/view-article-Mathematical-Aesthetics-in-Ragas.htmlMoitra, Abhirup. The Mathematical Harmony of Indian Classical Music. 2025.
Available at: https://abhirup-moitra-mathstat.netlify.app/probability/measure-music/measure-indianraga.html.
Accessed: August 3, 2025.
Further Research
Symmetric Measure Representation of Raga Bhairavi
Borel σ-Algebra in the Philosophy of Indian Classical Music
A Combinatorial Framework for Indian Classical Music
Thank You

https://abhirup-moitra-mathstat.netlify.app/