Code
# a (virtual) coin object
coin <- c("heads", "tails")
coin[1] "heads" "tails"We use cookies
We use cookies and other tracking technologies to improve your browsing experience on our website, to show you personalized content and targeted ads, to analyze our website traffic, and to understand where our visitors are coming from.
Abhirup Moitra
November 26, 2023
Simulation is a method used to examine the “what if” without having real data. We just make it up! We can use pre-programmed functions in R to simulate data from different probability distributions or we can design our own functions to simulate data from distributions not available in R.

we are going to consider a classic chance process (or chance experiment) of flipping a coin. Here you will learn how to implement code in R that simulates tossing a coin one or more times.
Think about a standard coin with two sides: heads and tails.

To toss a coin using R, we first need an object that plays the role of a coin. How do you create such a coin? Perhaps the simplest way to create a coin with two sides, "heads" and "tails", is with a character vector via the combine function c():
You can also create a numeric coin that shows 1 and 0 instead of "heads" and "tails":
Likewise, you can also create a logical coin that shows TRUE and FALSE instead of "heads" and "tails":
Once you have an R object that represents a coin, the next step involves learning how to simulate tossing the coin.
The important thing to keep in mind is that tossing a coin is a random experiment: you either get heads or tails. One way to simulate the action of tossing a coin in R is with the function sample() which lets you draw random samples, with or without replacement, of the elements in the input vector.
Here’s how to simulate a coin toss using sample() to take a random sample of size 1 of the elements in coin:
You use the argument size = 1 to specify that you want to take a sample of size 1 from the input vector coin.
By default, sample() takes a sample of the specified size without replacement. If size = 1, it does not really matter whether the sample is done with or without replacement.
To draw two elements without replacement, use sample() like this:
This is equivalent to calling sample() with the argument replace = FALSE:
What if you try to toss the coin three or four times?
sample(coin, size = 3)
Error in sample.int(length(x), size, replace, prob) :
cannot take a sample larger than the population when 'replace = FALSE'This is because the default behavior of sample() cannot draw more elements than the length of the input vector.
To be able to draw more elements, you need to sample with replacement, which is done by specifying the argument replace = TRUE, like this:
The way sample() works is by taking a random sample from the input vector. This means that every time you invoke sample() you will likely get a different output. For instance, when we run the following command twice, the output of the first call is different from the output in the second call, even though the command is exactly the same in both cases:
[1] "heads" "heads" "heads" "tails" "tails"[1] "heads" "tails" "tails" "tails" "tails"In order to make the examples replicable (so you can get the same output as mine), you need to specify what is called a random seed. This is done with the function set.seed(). By setting a seed, every time you use one of the random generator functions, like sample(), you will get the same values.
Last but not least, sample() comes with the argument prob which allows you to provide specific probabilities for each element in the input vector.
By default, prob = NULL, which means that every element has the same probability of being drawn. In the example of tossing a coin, the command sample(coin) is equivalent to sample(coin, prob = c(0.5, 0.5)). In the latter case we explicitly specify a probability of 50% chance of heads, and 50% chance of tails:
[1] "tails" "heads"[1] "tails" "heads"However, you can provide different probabilities for each of the elements in the input vector. For instance, to simulate a loaded coin with chance of heads 20%, and chance of tails 80%, set prob = c(0.2, 0.8) like so:
[1] "heads" "tails" "tails" "tails" "tails"Now that we have all the elements to toss a coin with R, let’s simulate flipping a coin 100 times, and then use the function table() to count the resulting number of "heads" and "tails":
flips
heads tails
50 50 In my case, I got 50 heads and 50 tails. Your results will probably be different than mine. Sometimes you will get more "heads", sometimes you will get more "tails", and sometimes you will get exactly 50 "heads" and 50 "tails".
Let’s run another series of 100 flips, and find the frequency of "heads" and "tails" with the help of the table() function:
flips
heads tails
50 50 To make things more interesting, let’s consider how the frequency of heads evolves over a series of n tosses (in this case n = num_flips).
With the vector heads_freq, we can graph the (cumulative) relative frequencies with a line-plot:
plot(heads_freq, # vector
type = 'l', # line type
lwd = 2, # width of line
col = 'tomato', # color of line
las = 1, # orientation of tick-mark labels
ylim = c(0, 1), # range of y-axis
xlab = "number of tosses", # x-axis label
ylab = "relative frequency") # y-axis label
abline(h = 0.5, col = 'gray50')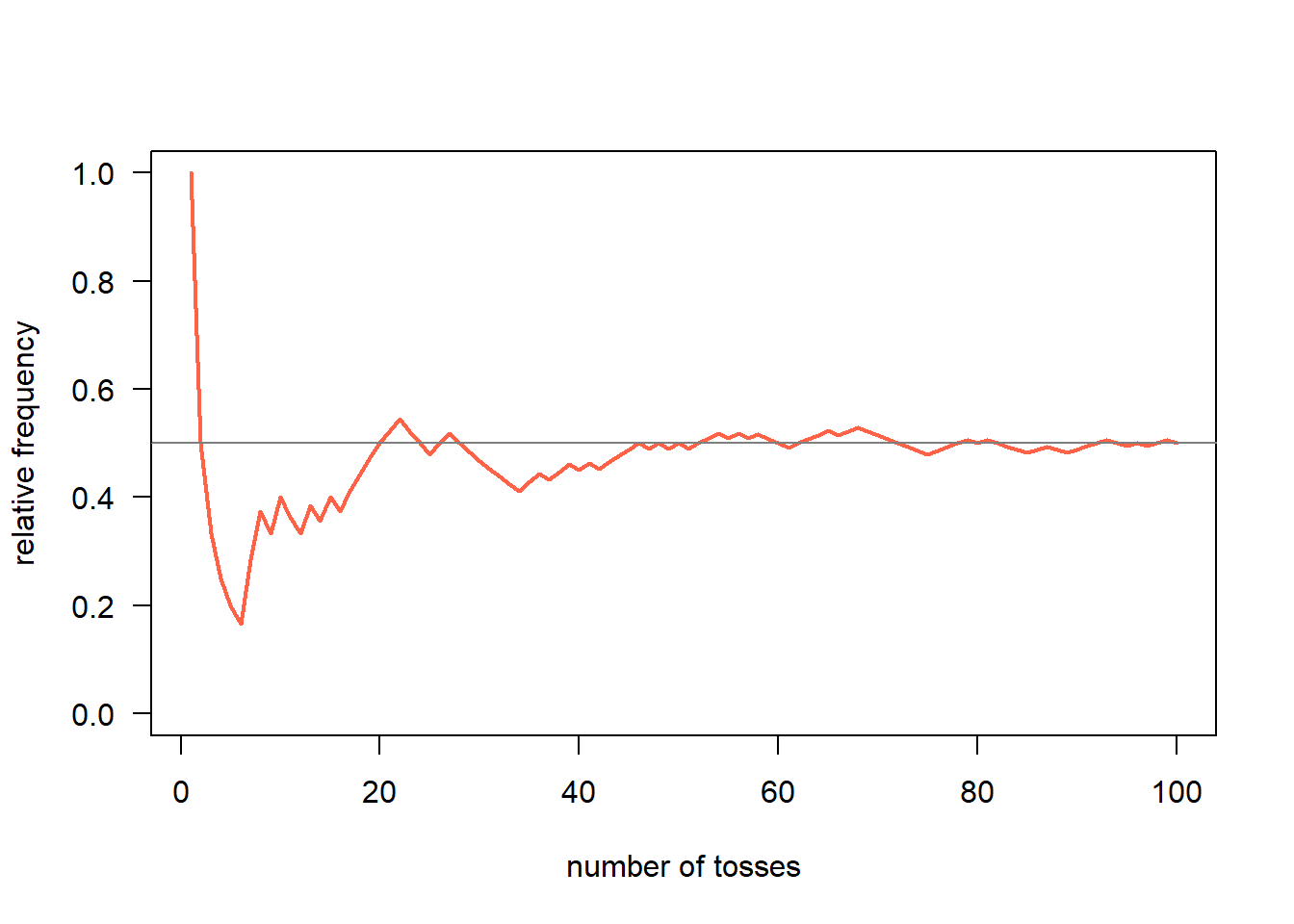
In the previous section, we wrote code to simulate tossing a coin multiple times. First, we created a virtual coin as a two-element vector. Secondly, we discussed how to use the function sample() to obtain a sample of a given size, with and without replacement. And finally, we put everything together: a coin object passed to sample(), to simulate tossing a coin.
[1] "tails" "heads" "tails" "tails" "tails"Our previous code works and we could get various sets of tosses of different sizes: 10 tosses, or 50, or 1000, or more:
As you can tell, even a single toss requires using the command sample(coin, size = 1, replace = TRUE) which is a bit long and requires some typing. Also, notice that we are repeating the call of sample() several times. This is the classic indication that we should instead write a function to encapsulate our code and reduce repetition.
toss() functionLet’s make things a little bit more complex but also more interesting. Instead of calling sample() every time we want to toss a coin, we can write a dedicated toss() function, something like this:
Recall that, to define a new function in R, you use the function function(). You need to specify a name for the function, and then assign function() to the chosen name. You also need to define optional arguments, which are basically the inputs of the function. And of course, you must write the code (i.e. the body) so the function does something when you use it. In summary:
Generally, you give a name to a function.
A function takes one or more inputs (or none), known as arguments.
The expressions forming the operations comprise the body of the function.
Usually, you wrap the body of the functions with curly braces.
A function returns a single value.
Once defined, you can use toss() like any other function in R:
[1] "tails"[1] "heads" "tails" "heads" "tails" "tails"Because we can make use of the prob argument inside sample(), we can make the toss() function more versatile by adding an argument that let us specify different probabilities for each side of a coin:
[1] "heads" "heads" "heads" "tails" "tails"[1] "heads" "heads" "heads" "tails" "heads"You should strive to always include documentation for your functions. In fact, writing documentation for your functions should become second nature. What does this mean? Documenting a function involves adding descriptions for the purpose of the function, the inputs it accepts, and the output it produces.
Description: what the function does
Input(s): what are the inputs or arguments
Output: what is the output or returned value
You can find some inspiration in the help() documentation when your search for a given function: e.g. help(mean)
A typical way to write documentation for a function is by adding comments for things like the description, input(s), output(s), like in the code below:
Here we will explore empirical probability using random samples. The two important functions to understand are sample() and replicate(). We use the sample function to set up our experiment, and replicate function to repeat it as many times as we want.
Setup the experiment where we roll two fair six sided die independently, and calculate the sum of the numbers that appear for each of them.
Use the replicate function to repeat this experiment 10000 times, store the output of the experiment in a variable “sum_die”.
[1] "Emperical probability = 0.4921"
---
title: "Simulation of Coin Tossing"
author: "Abhirup Moitra"
date: 2023-11-26
format:
html:
code-fold: true
code-tools: true
editor: visual
categories : [Mathematics, R Programming, Probability Theory]
image: coin-flip-flip.gif
---
# **Motivation Behind Simulation**
Simulation is a method used to examine the "what if" without having real data. We just make it up! We can use pre-programmed functions in R to simulate data from different probability distributions or we can design our own functions to simulate data from distributions not available in R.
{fig-align="center" width="214"}
we are going to consider a classic chance process (or chance experiment) of flipping a coin. Here you will learn how to implement code in R that simulates tossing a coin one or more times.
## 1.1 Coin object
Think about a standard coin with two sides: *heads* and *tails*.
{fig-align="center" width="404"}
To toss a coin using R, we first need an object that plays the role of a coin. How do you create such a coin? Perhaps the simplest way to create a coin with two sides, `"heads"` and `"tails"`, is with a character vector via the *combine* function `c()`:
```{r}
# a (virtual) coin object
coin <- c("heads", "tails")
coin
```
You can also create a *numeric* coin that shows `1` and `0` instead of `"heads"` and `"tails"`:
```{r}
num_coin <- c(1, 0)
num_coin
```
Likewise, you can also create a *logical* coin that shows `TRUE` and `FALSE` instead of `"heads"` and `"tails"`:
```{r}
log_coin <- c(TRUE, FALSE)
log_coin
```
## 1.2 Tossing a coin
Once you have an R object that represents a *coin*, the next step involves learning how to simulate tossing the coin.
The important thing to keep in mind is that tossing a coin is a random experiment: you either get heads or tails. One way to simulate the action of tossing a coin in R is with the function `sample()` which lets you draw random samples, with or without replacement, of the elements in the input vector.
Here's how to simulate a coin toss using `sample()` to take a random sample of size 1 of the elements in `coin`:
```{r}
# toss a coin
coin <- c('heads', 'tails')
sample(coin, size = 1)
```
You use the argument `size = 1` to specify that you want to take a sample of size 1 from the input vector `coin`.
### 1.2.1 Random Samples
By default, `sample()` takes a sample of the specified `size` **without replacement**. If `size = 1`, it does not really matter whether the sample is done with or without replacement.
To draw two elements **without** replacement, use `sample()` like this:
```{r}
# draw 2 elements without replacement
sample(coin, size = 2)
```
This is equivalent to calling `sample()` with the argument `replace = FALSE`:
```{r}
sample(coin, size = 2, replace = FALSE)
```
What if you try to toss the coin three or four times?
```
sample(coin, size = 3)
Error in sample.int(length(x), size, replace, prob) :
cannot take a sample larger than the population when 'replace = FALSE'
```
This is because the default behavior of `sample()` cannot draw more elements than the length of the input vector.
To be able to draw more elements, you need to sample **with replacement**, which is done by specifying the argument `replace = TRUE`, like this:
```{r}
# draw 4 elements with replacement
sample(coin, size = 4, replace = TRUE)
```
## 1.3 The Random Seed
The way `sample()` works is by taking a random sample from the input vector. This means that every time you invoke `sample()` you will likely get a different output. For instance, when we run the following command twice, the output of the first call is different from the output in the second call, even though the command is exactly the same in both cases:
```{r}
# five tosses
sample(coin, size = 5, replace = TRUE)
```
```{r}
# another five tosses
sample(coin, size = 5, replace = TRUE)
```
In order to make the examples replicable (so you can get the same output as mine), you need to specify what is called a **random seed**. This is done with the function `set.seed()`. By setting a *seed*, every time you use one of the random generator functions, like `sample()`, you will get the same values.
```{r}
# set random seed
set.seed(1257)
# toss a coin with replacement
sample(coin, size = 4, replace = TRUE)
```
## 1.4 Sampling with different probabilities
Last but not least, `sample()` comes with the argument `prob` which allows you to provide specific probabilities for each element in the input vector.
By default, `prob = NULL`, which means that every element has the same probability of being drawn. In the example of tossing a coin, the command `sample(coin)` is equivalent to `sample(coin, prob = c(0.5, 0.5))`. In the latter case we explicitly specify a probability of 50% chance of heads, and 50% chance of tails:
```{r}
# tossing a fair coin
coin <- c("heads", "tails")
sample(coin)
# equivalent
sample(coin, prob = c(0.5, 0.5))
```
However, you can provide different probabilities for each of the elements in the input vector. For instance, to simulate a **loaded** coin with chance of heads 20%, and chance of tails 80%, set `prob = c(0.2, 0.8)` like so:
```{r}
# tossing a loaded coin (20% heads, 80% tails)
sample(coin, size = 5, replace = TRUE, prob = c(0.2, 0.8))
```
### 1.4.1 Simulating tossing a coin
Now that we have all the elements to toss a coin with R, let's simulate flipping a coin 100 times, and then use the function `table()` to count the resulting number of `"heads"` and `"tails"`:
```{r}
# number of flips
num_flips <- 100
# flips simulation
coin <- c('heads', 'tails')
flips <- sample(coin, size = num_flips, replace = TRUE)
# number of heads and tails
freqs <- table(flips)
freqs
```
In my case, I got 50 heads and 50 tails. Your results will probably be different than mine. Sometimes you will get more `"heads"`, sometimes you will get more `"tails"`, and sometimes you will get exactly 50 `"heads"` and 50 `"tails"`.
Let's run another series of 100 flips, and find the frequency of `"heads"` and `"tails"` with the help of the `table()` function:
```{r}
# one more 100 flips
flips <- sample(coin, size = num_flips, replace = TRUE)
freqs <- table(flips)
freqs
```
To make things more interesting, let's consider how the frequency of `heads` evolves over a series of *n* tosses (in this case *n* = `num_flips`).
```{r}
heads_freq <- cumsum(flips == 'heads') / 1:num_flips
```
With the vector `heads_freq`, we can graph the (cumulative) relative frequencies with a line-plot:
```{r}
plot(heads_freq, # vector
type = 'l', # line type
lwd = 2, # width of line
col = 'tomato', # color of line
las = 1, # orientation of tick-mark labels
ylim = c(0, 1), # range of y-axis
xlab = "number of tosses", # x-axis label
ylab = "relative frequency") # y-axis label
abline(h = 0.5, col = 'gray50')
```
# 2 Tossing Function
## 2.1 Introduction
In the previous section, we wrote code to simulate tossing a coin multiple times. First, we created a virtual `coin` as a two-element vector. Secondly, we discussed how to use the function `sample()` to obtain a sample of a given size, with and without replacement. And finally, we put everything together: a `coin` object passed to `sample()`, to simulate tossing a coin.
```{r}
# tossing a coin 5 times
coin <- c("heads", "tails")
sample(coin, size = 5, replace = TRUE)
```
Our previous code works and we could get various sets of tosses of different sizes: 10 tosses, or 50, or 1000, or more:
```{r}
# various sets of tosses
flips1 <- sample(coin, size = 1, replace = TRUE)
flips10 <- sample(coin, size = 10, replace = TRUE)
flips50 <- sample(coin, size = 50, replace = TRUE)
flips1000 <- sample(coin, size = 1000, replace = TRUE)
```
As you can tell, even a single toss requires using the command `sample(coin, size = 1, replace = TRUE)` which is a bit long and requires some typing. Also, notice that we are repeating the call of `sample()` several times. This is the classic indication that we should instead write a function to encapsulate our code and reduce repetition.
## 2.2 A `toss()` function
Let's make things a little bit more complex but also more interesting. Instead of calling `sample()` every time we want to toss a coin, we can write a dedicated `toss()` function, something like this:
```{r}
# toss function (version 1)
toss <- function(x, times = 1) {
sample(x, size = times, replace = TRUE)
}
```
Recall that, to define a new function in R, you use the function `function()`. You need to specify a name for the function, and then assign `function()` to the chosen name. You also need to define optional arguments, which are basically the inputs of the function. And of course, you must write the code (i.e. the body) so the function does something when you use it. In summary:
- Generally, you give a name to a function.
- A function takes one or more inputs (or none), known as *arguments*.
- The expressions forming the operations comprise the **body** of the function.
- Usually, you wrap the body of the functions with curly braces.
- A function returns a single value.
Once defined, you can use `toss()` like any other function in R:
```{r}
# basic call
toss(coin)
# toss 5 times
toss(coin, 5)
```
Because we can make use of the `prob` argument inside `sample()`, we can make the `toss()` function more versatile by adding an argument that let us specify different probabilities for each side of a coin:
```{r}
# toss function (version 2)
toss <- function(x, times = 1, prob = NULL) {
sample(x, size = times, replace = TRUE, prob = prob)
}
# fair coin (default)
toss(coin, times = 5)
# laoded coin
toss(coin, times = 5, prob = c(0.8, 0.2))
```
## 2.3 Documenting Functions
You should strive to always include *documentation* for your functions. In fact, writing documentation for your functions should become second nature. What does this mean? Documenting a function involves adding descriptions for the purpose of the function, the inputs it accepts, and the output it produces.
- Description: what the function does
- Input(s): what are the inputs or arguments
- Output: what is the output or returned value
You can find some inspiration in the `help()` documentation when your search for a given function: e.g. `help(mean)`
A typical way to write documentation for a function is by adding comments for things like the description, input(s), output(s), like in the code below:
```{r}
# Description: tosses a coin
# Inputs
# x: coin object (a vector)
# times: how many times
# prob: probability values for each side
# Output
# vector of tosses
toss <- function(x, times = 1, prob = NULL) {
sample(x, size = times, replace = TRUE, prob = prob)
}
```
# **Probability and Counting**
Here we will explore empirical probability using random samples. The two important functions to understand are `sample()` and `replicate()`. We use the sample function to set up our experiment, and replicate function to repeat it as many times as we want.
# **1 Rolling Die**
## **1.1 Fair Die**
Setup the experiment where we roll two fair six sided die independently, and calculate the sum of the numbers that appear for each of them.
```{r}
roll2die <- sample(1:6,size=2,replace=TRUE)
roll2die
```
Use the replicate function to repeat this experiment 10000 times, store the output of the experiment in a variable "sum_die".
```{r}
sum_die = replicate(10000, sample (c(1,2,3,4,5,6),1) + sample (c(1,2,3,4,5,6),1))
exp_sum = seq(from = 2, to = 12, by = 2)
count = 0
for ( sum in sum_die ) {
if (sum %in% exp_sum) {
count = count + 1 }
}
print (paste("Emperical probability = ",count/10000))
```
{fig-align="center" width="315"}