An Exceptional Relationship between two Transcedental
\(e^{\pi}\) vs. \({\pi}^e\) : Which One is Bigger?
The mathematical and rigorous proof of this fact is that which is bigger \(e^{\pi}\) or \({\pi}^e\) is quite abstract. In this case, the mathematical arguments will not provide you coherent understanding until or unless we graphically plot this.
Here, we will use some graphical representation, and based on that we’ll draw the mathematical arguments and those mathematical arguments will lead you to the formal proof of this fact i.e., which is greater \(e^{\pi}\) or \({\pi}^e\).
From the Function \(y=\dfrac{1}{x}\)
Here, you can see that we are plotting the function \(y=\frac{1}{x}\) which is a decreasing function. When we look at the graph, the points are sloping down from left to right.
Now, if we plot \(x=e\) and draw a line to the graph, and note that \(\pi>e\). So we can draw a line to the graph when \(x= \pi\) as well.
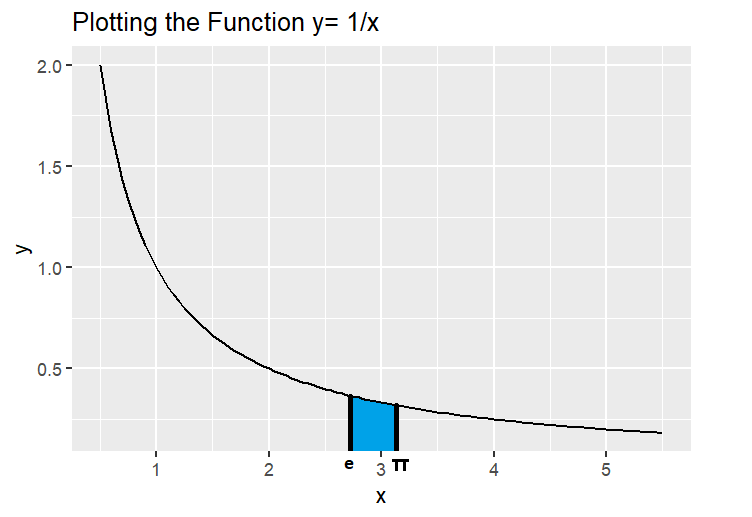
The area under the curve between \(e\) and \(\pi\) is represented as,
\[ \int_{e}^{\pi}\dfrac{1}{x}dx \]
Because the function is decreasing the rectangle (blue shaded rectangle in Fig 1.1) with height \(\frac{1}{e}(\pi-e)\) has a greater than the area under the curve which is the definite integral. i.e.,
\[\int_{e}^{\pi}\dfrac{1}{x}dx \le \frac{1}{e}(\pi-e)\]
Notice that the definite integral is \(ln(\pi)-1\) and the area of the rectangle can be simplified to \(\frac{\pi}{e}-1\) i.e.,
\[ln(\pi)-1=\int_{e}^{\pi}\dfrac{1}{x}dx \le \frac{1}{e}(\pi-e)= \dfrac{\pi}{e}-1\]
\[\implies ln(\pi)\le \dfrac{\pi}{e} \]
\[\implies e\ ln(\pi)\le \pi\]
\[\implies ln(\pi^{e})\le \pi\]
\[ \implies \boxed{\pi^e \le e^{\pi}} \] So, there you have it we used calculus on the curve \(y= \dfrac{1}{x}\) to convince ourselves that \(\pi^e\le e^{\pi}\).
From the Function \(\dfrac{ln(x)}{x}\)
So we have \(f(x)= \dfrac{ln(x)}{x}\)
\[ f^{'}(x)=\dfrac{1-ln(x)}{x^2} \]Hence, \(f(x)\) is a strictly monotone decreasing function for \(x≥e\) and a strictly monotone increasing function for \(x≤e\) .
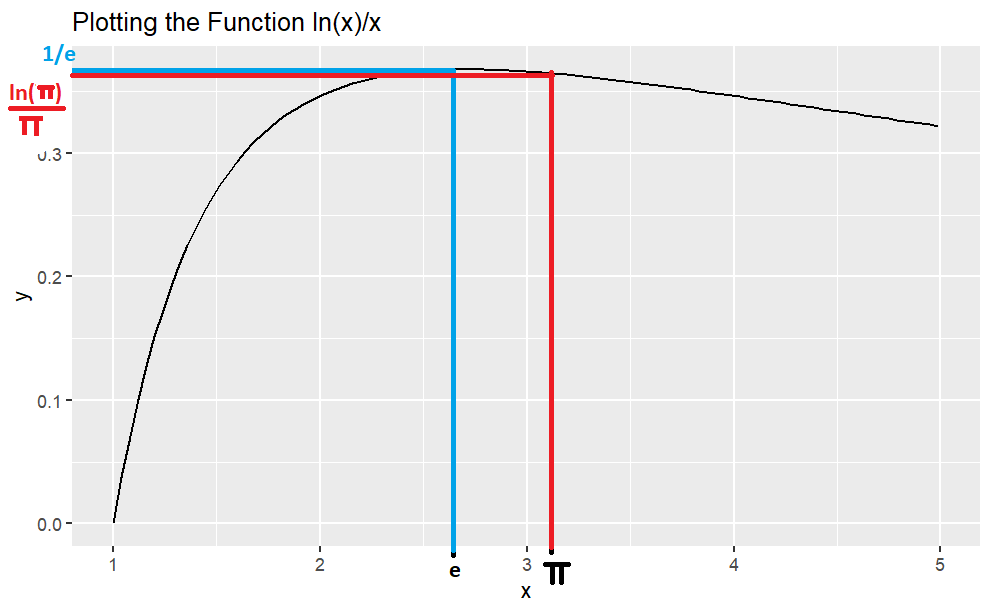
\[f^{'}(x)=0 \iff 1-ln(x)= 0 \iff x=e \]
Since \(π>3>e\)
\[ f(π)<f(e)⟹\dfrac{log(π)}{π}<\dfrac{log(e)}{e} \]
\[⟹ \boxed{π^{e}\le e^π}\] Henceforth we can also conclude that \(\boxed{π^{1/π}<e^{1/e}}\) . So we are done.
